Question Number 114875 by bobhans last updated on 21/Sep/20

A man sent 7 letters to his 7 friend . the letters are kept in addressed envelopes at random. the probability that 3 friends receive correct letters and 4 letters go to wrong destination is _ (old question unanswered)

Answered by PRITHWISH SEN 2 last updated on 21/Sep/20

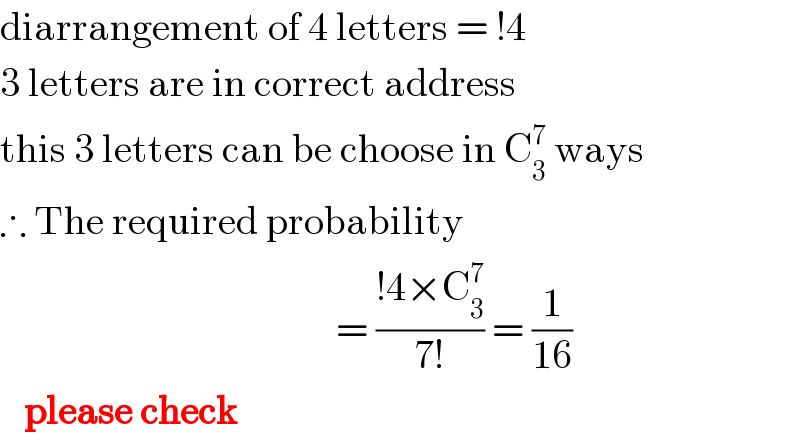
diarrangement of 4 letters = !4 3 letters are in correct address this 3 letters can be choose in C_3 ^7 ways ∴ The required probability = ((!4×C_3 ^7 )/(7!)) = (1/(16)) please check

Commented bymr W last updated on 21/Sep/20

correct!

Commented byPRITHWISH SEN 2 last updated on 21/Sep/20

thank you sir.

Commented bymr W last updated on 21/Sep/20

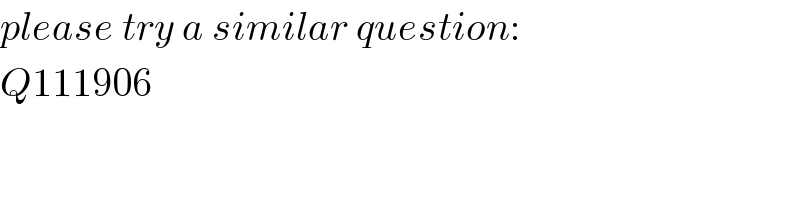
please try a similar question: Q111906

Commented byjohn santu last updated on 21/Sep/20

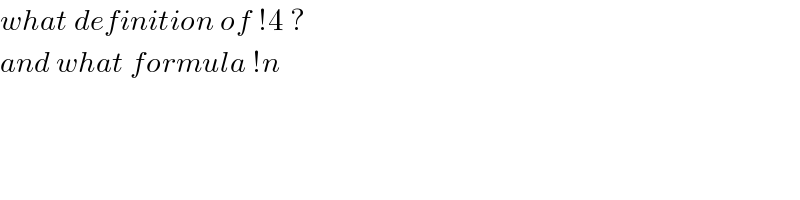
what definition of !4 ? and what formula !n

Commented byPRITHWISH SEN 2 last updated on 22/Sep/20

!n = n![1−(1/(1!))+(1/(2!))−(1/(3!))+.......+(−1)^n (1/(n!))]

Commented bymr W last updated on 27/Sep/20

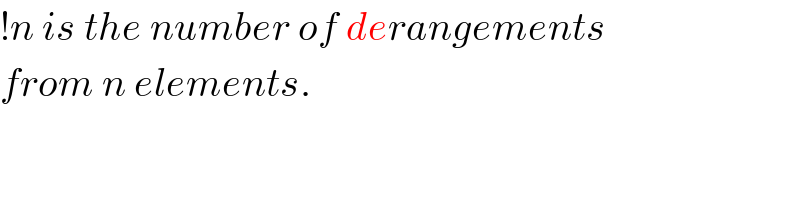
!n is the number of derangements from n elements.

Commented byPRITHWISH SEN 2 last updated on 22/Sep/20

sir please check Q 111906

Answered by soumyasaha last updated on 22/Sep/20

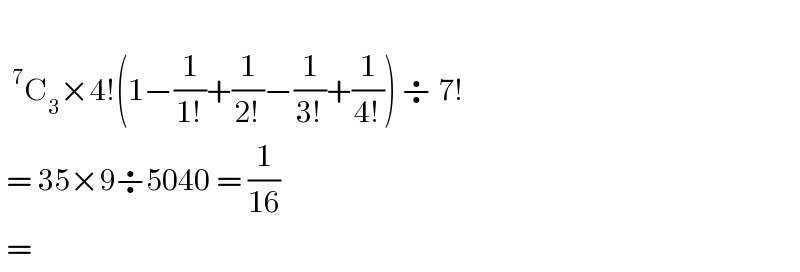
^7 C_3 ×4!(1−(1/(1!))+(1/(2!))−(1/(3!))+(1/(4!))) ÷ 7! = 35×9÷5040 = (1/(16)) =