
Question Number 114880 by manuel2456 last updated on 21/Sep/20
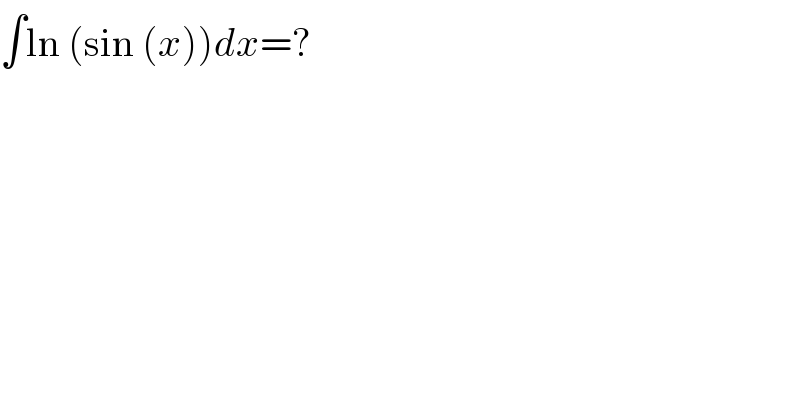
$$\int\mathrm{ln}\:\left(\mathrm{sin}\:\left({x}\right)\right){dx}=? \\ $$
Commented by MJS_new last updated on 21/Sep/20

$$\mathrm{similar}\:\mathrm{to}\:\mathrm{question}\:\mathrm{113634} \\ $$
Answered by mathdave last updated on 23/Sep/20

$${solution}\: \\ $$$${from}\:{binomial}\:{theorem} \\ $$$${let}\:\:\:\frac{\mathrm{1}}{\mathrm{1}−{y}}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{y}^{{n}−\mathrm{1}} \:{or}\:\mathrm{ln}\left(\mathrm{1}−{y}\right)=−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{y}^{{n}} }{{n}} \\ $$$${put}\:{y}={e}^{{i}\mathrm{2}{x}} \\ $$$$\mathrm{ln}\left(\mathrm{1}−{e}^{{i}\mathrm{2}{x}} \right)=−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{e}^{{i}\mathrm{2}{nx}} }{{n}} \\ $$$$\mathrm{ln}\left(\mathrm{1}−\left(\mathrm{cos2}{x}+{i}\mathrm{sin2}{x}\right)\right)=−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\left(\mathrm{cos}\left(\mathrm{2}{nx}\right)+{i}\mathrm{sin}\left(\mathrm{2}{nx}\right)\right) \\ $$$${but}\:\mathrm{2sin}^{\mathrm{2}} {x}=\mathrm{1}−\mathrm{cos2}{x}\:\:{and}\:\mathrm{sin2}{x}=\mathrm{2sin}{x}\mathrm{cos}{x} \\ $$$$\mathrm{ln}\left(\mathrm{2sin}^{\mathrm{2}} {x}−{i}\mathrm{2sin}{x}\mathrm{cos}{x}\right)=−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{cos}\left(\mathrm{2}{nx}\right)}{{n}}−{i}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{2}{nx}\right)}{{n}} \\ $$$$\mathrm{ln}\left(\mathrm{2sin}{x}\left(\mathrm{sin}{x}−{i}\mathrm{cos}{x}\right)\right)=−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{cos}\left(\mathrm{2}{nx}\right)}{{n}}−{i}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{2}{nx}\right)}{{n}} \\ $$$$\mathrm{ln}\left(\mathrm{2sin}{x}\right)+\mathrm{ln}\left(\mathrm{sin}{x}−{i}\mathrm{cos}{x}\right)=−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{cos}\left(\mathrm{2}{nx}\right)}{{n}}−{i}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{2}{nx}\right)}{{n}} \\ $$$${let} \\ $$$$\mathrm{ln}\left(−{i}\left(−\frac{\mathrm{1}}{{i}}\mathrm{sin}{x}+\mathrm{cos}{x}\right)\right)=\mathrm{ln}\left(−{i}\left(\mathrm{cos}{x}−\frac{\mathrm{1}}{{i}}\mathrm{sin}{x}\right)\right)=\mathrm{ln}\left(−{i}\left(\mathrm{cos}{x}+{i}\mathrm{sin}{x}\right)\right)=\mathrm{ln}\left(−{i}.{e}^{{ix}} \right) \\ $$$${but} \\ $$$$\mathrm{ln}\left(−{i}.{e}^{{ix}} \right)=\mathrm{ln}\left(−\mathrm{1}\right)+\mathrm{ln}\left({e}^{{ix}} \right)={ix}+\mathrm{ln}\left(−{i}\right)={ix}−{i}\frac{\pi}{\mathrm{2}}=−{i}\left(\frac{\pi}{\mathrm{2}}−{x}\right) \\ $$$$\therefore\mathrm{ln}\left(\mathrm{2sin}{x}\right)−{i}\left(\frac{\pi}{\mathrm{2}}−{x}\right)=−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{cos}\left(\mathrm{2}{nx}\right)}{{n}}−{i}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{2}{nx}\right)}{{n}} \\ $$$${by}\:{equating}\:{real}\:{and}\:{imaginary}\:{part} \\ $$$$\mathrm{ln}\left(\mathrm{2sin}{x}\right)=−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{cos}\left(\mathrm{2}{nx}\right)}{{n}} \\ $$$$\mathrm{ln2}+\mathrm{ln}\left(\mathrm{sin}{x}\right)=−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{cos}\left(\mathrm{2}{nx}\right)}{{n}} \\ $$$$\mathrm{ln}\left(\mathrm{sin}{x}\right)=−\mathrm{ln2}−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{cos}\left(\mathrm{2}{nx}\right)}{{n}}\:......\left(\mathrm{1}\right)\:\: \\ $$$$\because\int\mathrm{ln}\left(\mathrm{sin}{x}\right){dx}=−\mathrm{ln2}\int{dx}−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\int\mathrm{cos}\left(\mathrm{2}{nx}\right){dx} \\ $$$$\because\int\mathrm{ln}\left(\mathrm{sin}{x}\right){dx}=−{x}\mathrm{ln2}−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} }\mathrm{sin}\left(\mathrm{2}{nx}\right) \\ $$$${by}\:{mathdave}\left(\mathrm{23}/\mathrm{09}/\mathrm{2020}\right) \\ $$$$ \\ $$
Commented by Tawa11 last updated on 06/Sep/21

$$\mathrm{grest}\:\mathrm{sir} \\ $$
