
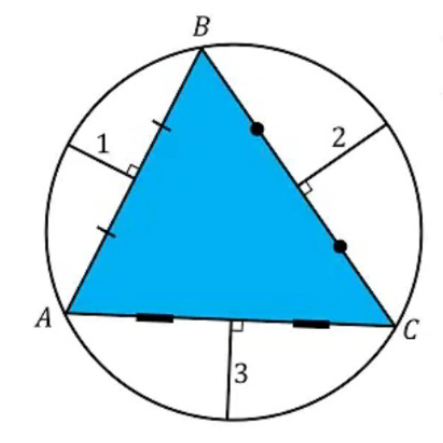
Question Number 114906 by mr W last updated on 21/Sep/20
Commented by MJS_new last updated on 22/Sep/20
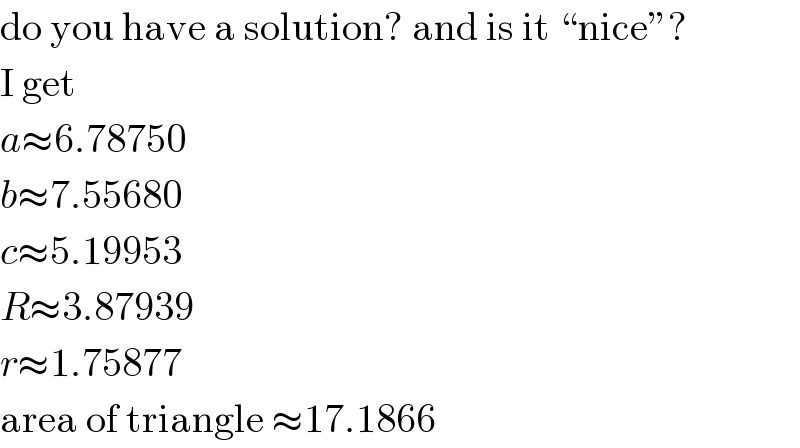
$$\mathrm{do}\:\mathrm{you}\:\mathrm{have}\:\mathrm{a}\:\mathrm{solution}?\:\mathrm{and}\:\mathrm{is}\:\mathrm{it}\:``\mathrm{nice}''? \\ $$$$\mathrm{I}\:\mathrm{get} \\ $$$${a}\approx\mathrm{6}.\mathrm{78750} \\ $$$${b}\approx\mathrm{7}.\mathrm{55680} \\ $$$${c}\approx\mathrm{5}.\mathrm{19953} \\ $$$${R}\approx\mathrm{3}.\mathrm{87939} \\ $$$${r}\approx\mathrm{1}.\mathrm{75877} \\ $$$$\mathrm{area}\:\mathrm{of}\:\mathrm{triangle}\:\approx\mathrm{17}.\mathrm{1866} \\ $$
Answered by mr W last updated on 21/Sep/20
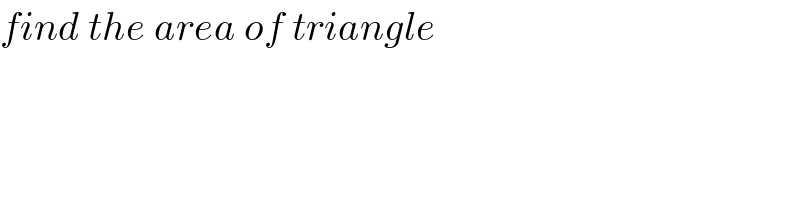
$${find}\:{the}\:{area}\:{of}\:{triangle} \\ $$
Answered by bobhans last updated on 22/Sep/20
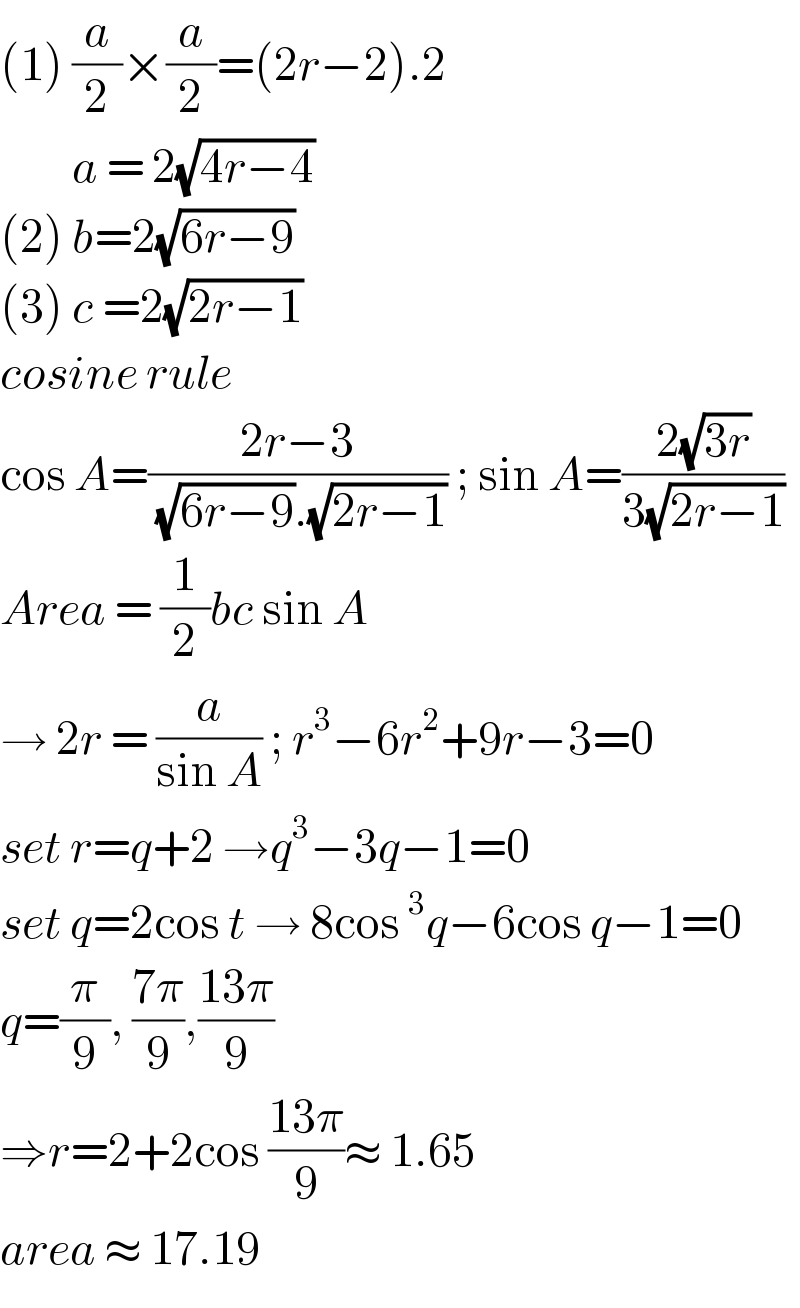
$$\left(\mathrm{1}\right)\:\frac{{a}}{\mathrm{2}}×\frac{{a}}{\mathrm{2}}=\left(\mathrm{2}{r}−\mathrm{2}\right).\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:{a}\:=\:\mathrm{2}\sqrt{\mathrm{4}{r}−\mathrm{4}} \\ $$$$\left(\mathrm{2}\right)\:{b}=\mathrm{2}\sqrt{\mathrm{6}{r}−\mathrm{9}} \\ $$$$\left(\mathrm{3}\right)\:{c}\:=\mathrm{2}\sqrt{\mathrm{2}{r}−\mathrm{1}} \\ $$$${cosine}\:{rule} \\ $$$$\mathrm{cos}\:{A}=\frac{\mathrm{2}{r}−\mathrm{3}}{\:\sqrt{\mathrm{6}{r}−\mathrm{9}}.\sqrt{\mathrm{2}{r}−\mathrm{1}}}\:;\:\mathrm{sin}\:{A}=\frac{\mathrm{2}\sqrt{\mathrm{3}{r}}}{\mathrm{3}\sqrt{\mathrm{2}{r}−\mathrm{1}}} \\ $$$${Area}\:=\:\frac{\mathrm{1}}{\mathrm{2}}{bc}\:\mathrm{sin}\:{A} \\ $$$$\rightarrow\:\mathrm{2}{r}\:=\:\frac{{a}}{\mathrm{sin}\:{A}}\:;\:{r}^{\mathrm{3}} −\mathrm{6}{r}^{\mathrm{2}} +\mathrm{9}{r}−\mathrm{3}=\mathrm{0} \\ $$$${set}\:{r}={q}+\mathrm{2}\:\rightarrow{q}^{\mathrm{3}} −\mathrm{3}{q}−\mathrm{1}=\mathrm{0} \\ $$$${set}\:{q}=\mathrm{2cos}\:{t}\:\rightarrow\:\mathrm{8cos}\:^{\mathrm{3}} {q}−\mathrm{6cos}\:{q}−\mathrm{1}=\mathrm{0} \\ $$$${q}=\frac{\pi}{\mathrm{9}},\:\frac{\mathrm{7}\pi}{\mathrm{9}},\frac{\mathrm{13}\pi}{\mathrm{9}} \\ $$$$\Rightarrow{r}=\mathrm{2}+\mathrm{2cos}\:\frac{\mathrm{13}\pi}{\mathrm{9}}\approx\:\mathrm{1}.\mathrm{65} \\ $$$${area}\:\approx\:\mathrm{17}.\mathrm{19} \\ $$
Commented by mr W last updated on 22/Sep/20
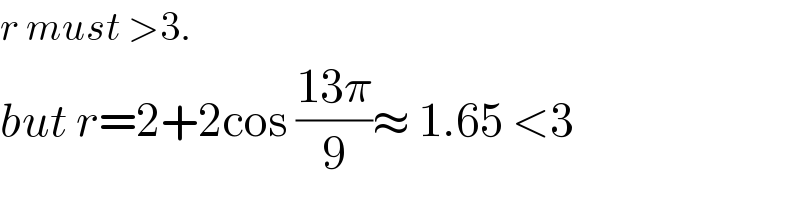
$${r}\:{must}\:>\mathrm{3}. \\ $$$${but}\:{r}=\mathrm{2}+\mathrm{2cos}\:\frac{\mathrm{13}\pi}{\mathrm{9}}\approx\:\mathrm{1}.\mathrm{65}\:<\mathrm{3} \\ $$
Answered by mr W last updated on 22/Sep/20
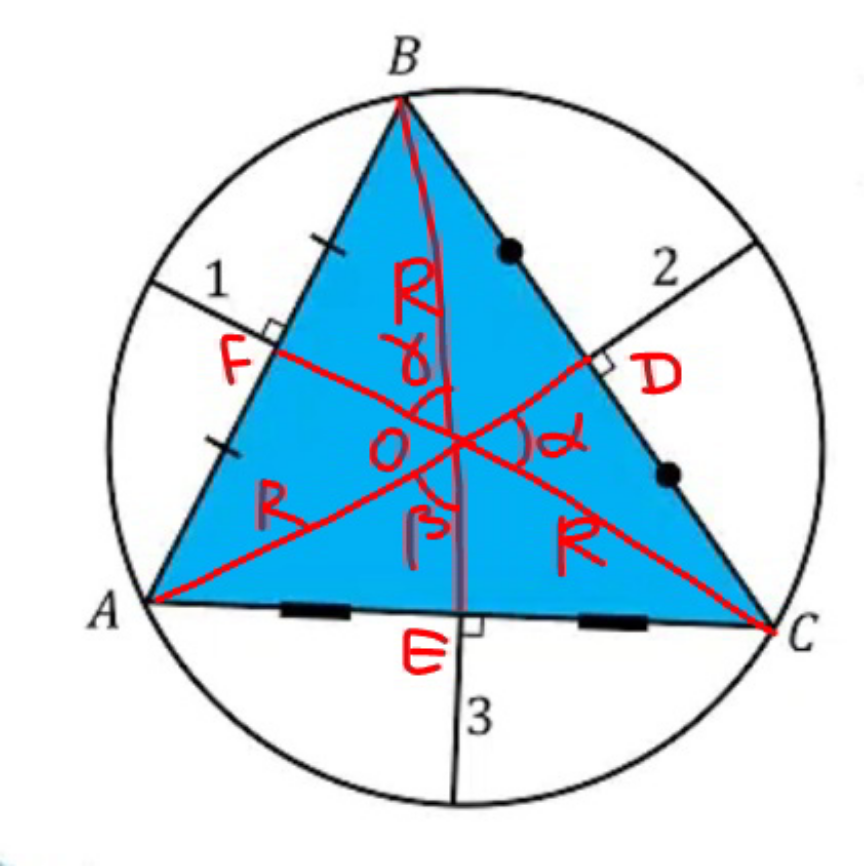
Commented by mr W last updated on 22/Sep/20
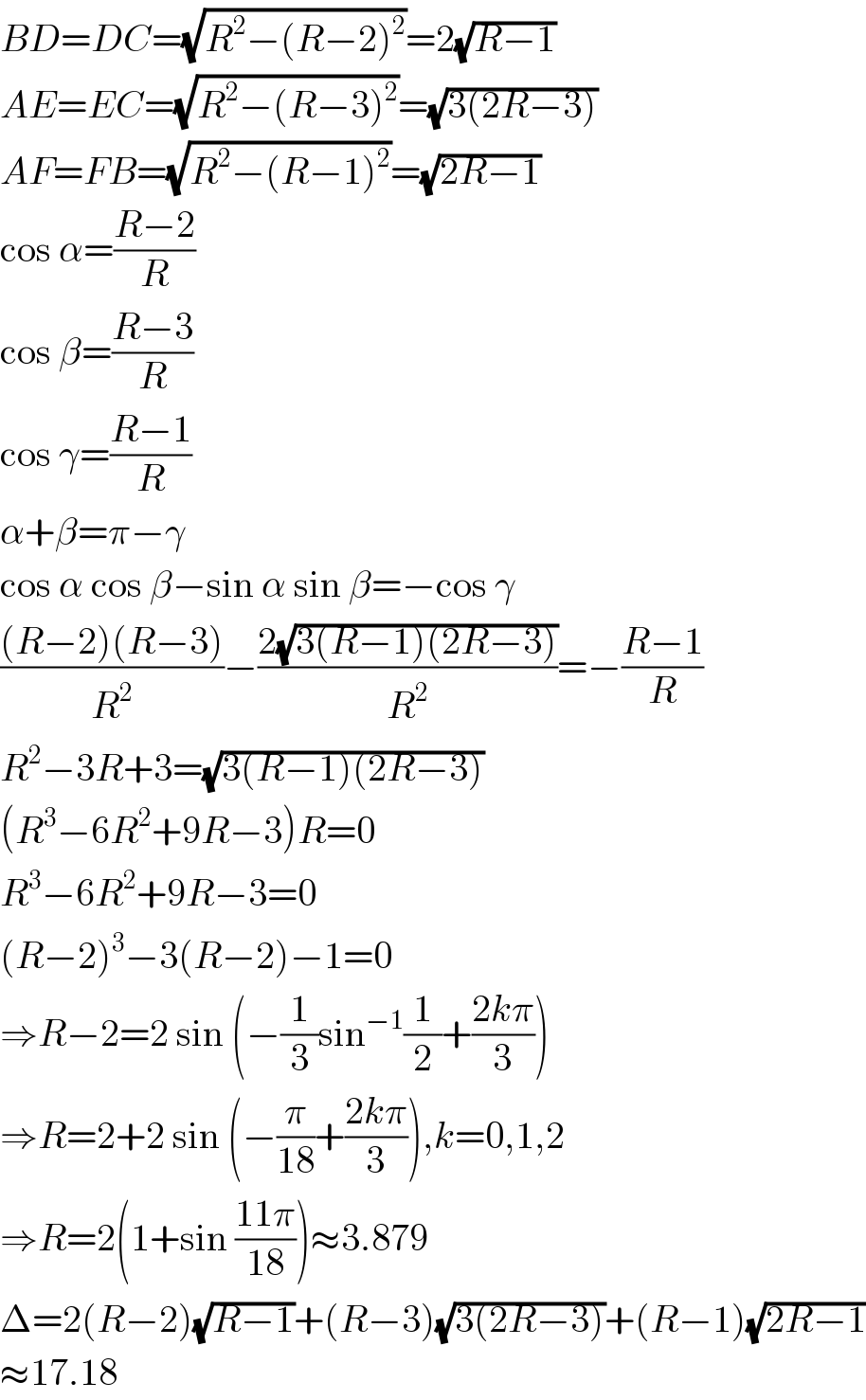
$${BD}={DC}=\sqrt{{R}^{\mathrm{2}} −\left({R}−\mathrm{2}\right)^{\mathrm{2}} }=\mathrm{2}\sqrt{{R}−\mathrm{1}} \\ $$$${AE}={EC}=\sqrt{{R}^{\mathrm{2}} −\left({R}−\mathrm{3}\right)^{\mathrm{2}} }=\sqrt{\mathrm{3}\left(\mathrm{2}{R}−\mathrm{3}\right)} \\ $$$${AF}={FB}=\sqrt{{R}^{\mathrm{2}} −\left({R}−\mathrm{1}\right)^{\mathrm{2}} }=\sqrt{\mathrm{2}{R}−\mathrm{1}} \\ $$$$\mathrm{cos}\:\alpha=\frac{{R}−\mathrm{2}}{{R}} \\ $$$$\mathrm{cos}\:\beta=\frac{{R}−\mathrm{3}}{{R}} \\ $$$$\mathrm{cos}\:\gamma=\frac{{R}−\mathrm{1}}{{R}} \\ $$$$\alpha+\beta=\pi−\gamma \\ $$$$\mathrm{cos}\:\alpha\:\mathrm{cos}\:\beta−\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta=−\mathrm{cos}\:\gamma \\ $$$$\frac{\left({R}−\mathrm{2}\right)\left({R}−\mathrm{3}\right)}{{R}^{\mathrm{2}} }−\frac{\mathrm{2}\sqrt{\mathrm{3}\left({R}−\mathrm{1}\right)\left(\mathrm{2}{R}−\mathrm{3}\right)}}{{R}^{\mathrm{2}} }=−\frac{{R}−\mathrm{1}}{{R}} \\ $$$${R}^{\mathrm{2}} −\mathrm{3}{R}+\mathrm{3}=\sqrt{\mathrm{3}\left({R}−\mathrm{1}\right)\left(\mathrm{2}{R}−\mathrm{3}\right)} \\ $$$$\left({R}^{\mathrm{3}} −\mathrm{6}{R}^{\mathrm{2}} +\mathrm{9}{R}−\mathrm{3}\right){R}=\mathrm{0} \\ $$$${R}^{\mathrm{3}} −\mathrm{6}{R}^{\mathrm{2}} +\mathrm{9}{R}−\mathrm{3}=\mathrm{0} \\ $$$$\left({R}−\mathrm{2}\right)^{\mathrm{3}} −\mathrm{3}\left({R}−\mathrm{2}\right)−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{R}−\mathrm{2}=\mathrm{2}\:\mathrm{sin}\:\left(−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{2}{k}\pi}{\mathrm{3}}\right) \\ $$$$\Rightarrow{R}=\mathrm{2}+\mathrm{2}\:\mathrm{sin}\:\left(−\frac{\pi}{\mathrm{18}}+\frac{\mathrm{2}{k}\pi}{\mathrm{3}}\right),{k}=\mathrm{0},\mathrm{1},\mathrm{2} \\ $$$$\Rightarrow{R}=\mathrm{2}\left(\mathrm{1}+\mathrm{sin}\:\frac{\mathrm{11}\pi}{\mathrm{18}}\right)\approx\mathrm{3}.\mathrm{879} \\ $$$$\Delta=\mathrm{2}\left({R}−\mathrm{2}\right)\sqrt{{R}−\mathrm{1}}+\left({R}−\mathrm{3}\right)\sqrt{\mathrm{3}\left(\mathrm{2}{R}−\mathrm{3}\right)}+\left({R}−\mathrm{1}\right)\sqrt{\mathrm{2}{R}−\mathrm{1}} \\ $$$$\approx\mathrm{17}.\mathrm{18} \\ $$
