Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 114959 by mathdave last updated on 22/Sep/20

long time question proposed by math abdo ∫_0 ^∞ ((lnx)/(1+x^2 +x^4 ))dx

$${long}\:{time}\:{question}\:{proposed}\:{by} \\ $$$${math}\:{abdo} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}{x}}{\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} }{dx} \\ $$$$ \\ $$

Answered by mathdave last updated on 22/Sep/20

solution let I=∫_0 ^∞ ((lnx)/(1+x^2 +x^4 ))dx=∫_0 ^1 ((lnx)/(1+x^2 +x^4 ))dx+∫_1 ^∞ ((lnx)/(1+x^2 +x^4 ))dx=A+B puttting x=(1/x) into integral B I=∫_0 ^1 ((lnx)/(1+x^2 +x^4 ))dx−∫_0 ^1 ((x^2 lnx)/(1+x^2 +x^(4 ) ))dx=A−B let A=∫_0 ^1 ((lnx)/(1+x^2 +x^4 ))dx=∫_0 ^1 ((lnx)/(1−x^6 ))dx−∫_0 ^1 ((x^2 lnx)/(1−x^6 ))dx A=Σ_(n=0) ^∞ ∫_0 ^1 x^(6n) .lnxdx−Σ_(n=0) ^∞ ∫_0 ^1 x^2 .x^(6n) .lnxdx A=Σ_(n=0) ^∞ (∂/∂a)∣_(a=1) ∫_0 ^1 x^(6n) .x^(a−1) dx−Σ_(n=0) ^∞ (∂/∂a)∣_(a=1) ∫_0 ^1 x^(6n+2) .x^(a−1) dx A=Σ_(n=0) ^∞ (∂/∂a)∣_(a=1) ((1/(6n+a)))−Σ_(n=0) ^∞ (∂/∂a)∣_(a=1) ((1/(6n+2+a))) A=−Σ_(n=0) ^∞ (1/((6n+1)^2 ))+Σ_(n=0) ^∞ (1/((6n+3)^2 ))=−(1/(36))Σ_(n=0) ^∞ (1/((n+(1/6))^2 ))+(1/(36))Σ_(n=0) ^∞ (1/((n+(1/2))^2 )) A=−(1/(36))ψ^1 ((1/6))+(1/(36))ψ^1 ((1/2))...........(1) and B=∫_0 ^1 ((x^2 lnx)/(1+x^2 +x^4 ))dx=∫_0 ^1 ((x^2 lnx)/(1−x^6 ))dx−∫_0 ^1 ((x^4 lnx)/(1−x^6 ))dx B=Σ_(n=0) ^∞ ∫_0 ^1 x^2 .lnx.x^(6n) dx−Σ_(n=0) ^∞ ∫_0 ^1 x^4 .lnx.x^(6n) dx B=Σ_(n=0) ^∞ (∂/∂a)∣_(a=1) ∫_0 ^1 x^(6n+2) .x^(a−1) dx−Σ_(n=0) ^∞ (∂/∂a)∣_(a=1) ∫_0 ^1 x^(6n+4) .x^(a−1) dx B=Σ_(n=0) ^∞ (∂/∂a)∣_(a=1) ((1/(6n+2+a)))−Σ_(n=0) ^∞ (∂/∂a)∣_(a=1) ((1/(6n+4+a))) B=−Σ_(n=0) ^∞ (1/((6n+3)^2 ))+Σ_(n=0) ^∞ (1/((6n+5)^2 ))=−(1/(36))Σ_(n=0) ^∞ (1/((n+(1/2))^2 ))+(1/(36))Σ_(n=0) ^∞ (1/((n+(5/6))^2 )) B=−(1/(36))ψ^1 ((1/2))+(1/(36))ψ^1 ((5/6))........(2) but I=A−B I=−(1/(36))ψ^1 ((1/6))+(1/(36))ψ^1 ((1/2))−(−(1/(36))ψ^1 ((1/2))+(1/(36))ψ^1 ((5/6))) I=(1/(18))ψ^1 ((1/2))−(1/(36))[ψ^1 ((1/6))+ψ^1 (1−(1/6))] using ψ^1 (z)+ψ^1 (1−z)=(π^2 /(sin^2 (πz))) ψ^1 ((1/6))+ψ^1 (1−(1/6))=(π^2 /([sin((π/6))]^2 ))=4π^2 I=(1/(18))ψ^1 ((1/2))−((4π^2 )/(36))=(1/(18))((π^2 /2))−((4π^2 )/(36))=−((3π^2 )/(36))=−(π^2 /(12)) ∵∫_0 ^∞ ((lnx)/(1+x^2 +x^4 ))dx=−(π^2 /(12)) b8y nathdave(22/09/2020)

$${solution} \\ $$$${let} \\ $$$${I}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}{x}}{\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} }{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}{x}}{\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} }{dx}+\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{ln}{x}}{\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} }{dx}={A}+{B} \\ $$$${puttting}\:\:{x}=\frac{\mathrm{1}}{{x}}\:\:{into}\:{integral}\:{B} \\ $$$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}{x}}{\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} }{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} \mathrm{ln}{x}}{\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}\:} }{dx}={A}−{B} \\ $$$${let} \\ $$$${A}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}{x}}{\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} }{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}{x}}{\mathrm{1}−{x}^{\mathrm{6}} }{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} \mathrm{ln}{x}}{\mathrm{1}−{x}^{\mathrm{6}} }{dx} \\ $$$${A}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{6}{n}} .\mathrm{ln}{xdx}−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}} .{x}^{\mathrm{6}{n}} .\mathrm{ln}{xdx} \\ $$$${A}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\partial}{\partial{a}}\mid_{{a}=\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{6}{n}} .{x}^{{a}−\mathrm{1}} {dx}−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\partial}{\partial{a}}\mid_{{a}=\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{6}{n}+\mathrm{2}} .{x}^{{a}−\mathrm{1}} {dx} \\ $$$${A}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\partial}{\partial{a}}\mid_{{a}=\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{6}{n}+{a}}\right)−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\partial}{\partial{a}}\mid_{{a}=\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{6}{n}+\mathrm{2}+{a}}\right) \\ $$$${A}=−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{6}{n}+\mathrm{1}\right)^{\mathrm{2}} }+\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{6}{n}+\mathrm{3}\right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{36}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{1}}{\mathrm{6}}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{36}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$${A}=−\frac{\mathrm{1}}{\mathrm{36}}\psi^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{6}}\right)+\frac{\mathrm{1}}{\mathrm{36}}\psi^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)...........\left(\mathrm{1}\right)\:{and}\: \\ $$$${B}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} \mathrm{ln}{x}}{\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} }{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} \mathrm{ln}{x}}{\mathrm{1}−{x}^{\mathrm{6}} }{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{4}} \mathrm{ln}{x}}{\mathrm{1}−{x}^{\mathrm{6}} }{dx} \\ $$$${B}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}} .\mathrm{ln}{x}.{x}^{\mathrm{6}{n}} {dx}−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{4}} .\mathrm{ln}{x}.{x}^{\mathrm{6}{n}} {dx} \\ $$$${B}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\partial}{\partial{a}}\mid_{{a}=\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{6}{n}+\mathrm{2}} .{x}^{{a}−\mathrm{1}} {dx}−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\partial}{\partial{a}}\mid_{{a}=\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{6}{n}+\mathrm{4}} .{x}^{{a}−\mathrm{1}} {dx} \\ $$$${B}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\partial}{\partial{a}}\mid_{{a}=\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{6}{n}+\mathrm{2}+{a}}\right)−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\partial}{\partial{a}}\mid_{{a}=\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{6}{n}+\mathrm{4}+{a}}\right) \\ $$$${B}=−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{6}{n}+\mathrm{3}\right)^{\mathrm{2}} }+\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{6}{n}+\mathrm{5}\right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{36}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{36}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{5}}{\mathrm{6}}\right)^{\mathrm{2}} } \\ $$$${B}=−\frac{\mathrm{1}}{\mathrm{36}}\psi^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{36}}\psi^{\mathrm{1}} \left(\frac{\mathrm{5}}{\mathrm{6}}\right)........\left(\mathrm{2}\right) \\ $$$${but}\:\:{I}={A}−{B} \\ $$$${I}=−\frac{\mathrm{1}}{\mathrm{36}}\psi^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{6}}\right)+\frac{\mathrm{1}}{\mathrm{36}}\psi^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\left(−\frac{\mathrm{1}}{\mathrm{36}}\psi^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{36}}\psi^{\mathrm{1}} \left(\frac{\mathrm{5}}{\mathrm{6}}\right)\right) \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{18}}\psi^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{36}}\left[\psi^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{6}}\right)+\psi^{\mathrm{1}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{6}}\right)\right] \\ $$$${using}\:\:\psi^{\mathrm{1}} \left({z}\right)+\psi^{\mathrm{1}} \left(\mathrm{1}−{z}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{sin}^{\mathrm{2}} \left(\pi{z}\right)} \\ $$$$\psi^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{6}}\right)+\psi^{\mathrm{1}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{6}}\right)=\frac{\pi^{\mathrm{2}} }{\left[\mathrm{sin}\left(\frac{\pi}{\mathrm{6}}\right)\right]^{\mathrm{2}} }=\mathrm{4}\pi^{\mathrm{2}} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{18}}\psi^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\frac{\mathrm{4}\pi^{\mathrm{2}} }{\mathrm{36}}=\frac{\mathrm{1}}{\mathrm{18}}\left(\frac{\pi^{\mathrm{2}} }{\mathrm{2}}\right)−\frac{\mathrm{4}\pi^{\mathrm{2}} }{\mathrm{36}}=−\frac{\mathrm{3}\pi^{\mathrm{2}} }{\mathrm{36}}=−\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$$$\because\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}{x}}{\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} }{dx}=−\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$$${b}\mathrm{8}{y}\:{nathdave}\left(\mathrm{22}/\mathrm{09}/\mathrm{2020}\right) \\ $$

Commented by I want to learn more last updated on 23/Sep/20

And sir, does the identity has proof?

$$\mathrm{And}\:\mathrm{sir},\:\mathrm{does}\:\mathrm{the}\:\mathrm{identity}\:\mathrm{has}\:\mathrm{proof}? \\ $$

Commented by I want to learn more last updated on 23/Sep/20

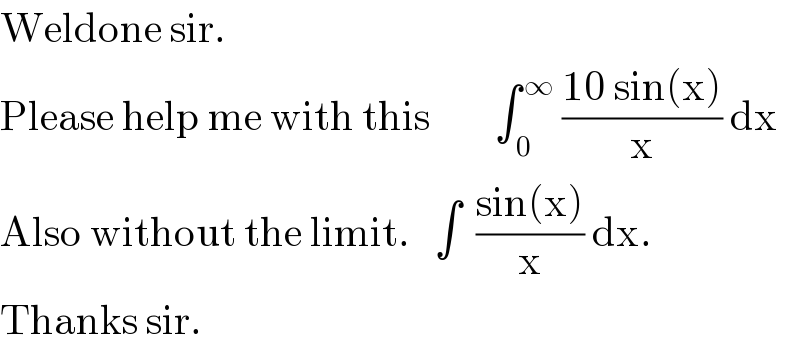
Weldone sir. Please help me with this ∫_( 0) ^( ∞) ((10 sin(x))/x) dx Also without the limit. ∫ ((sin(x))/x) dx. Thanks sir.

$$\mathrm{Weldone}\:\mathrm{sir}. \\ $$$$\mathrm{Please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{with}\:\mathrm{this}\:\:\:\:\:\:\:\:\int_{\:\mathrm{0}} ^{\:\infty} \:\frac{\mathrm{10}\:\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{x}}\:\mathrm{dx} \\ $$$$\mathrm{Also}\:\mathrm{without}\:\mathrm{the}\:\mathrm{limit}.\:\:\:\int\:\:\frac{\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{x}}\:\mathrm{dx}. \\ $$$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$

Commented by mathdave last updated on 23/Sep/20

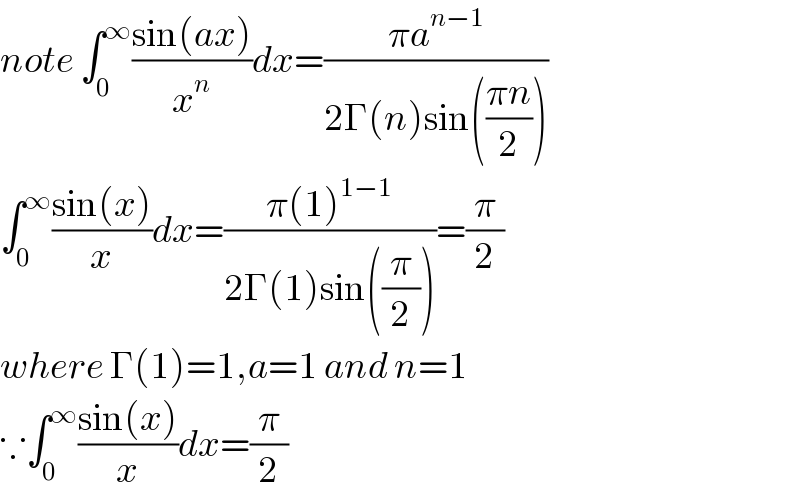
note ∫_0 ^∞ ((sin(ax))/x^n )dx=((πa^(n−1) )/(2Γ(n)sin(((πn)/2)))) ∫_0 ^∞ ((sin(x))/x)dx=((π(1)^(1−1) )/(2Γ(1)sin((π/2))))=(π/2) where Γ(1)=1,a=1 and n=1 ∵∫_0 ^∞ ((sin(x))/x)dx=(π/2)

$${note}\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}\left({ax}\right)}{{x}^{{n}} }{dx}=\frac{\pi{a}^{{n}−\mathrm{1}} }{\mathrm{2}\Gamma\left({n}\right)\mathrm{sin}\left(\frac{\pi{n}}{\mathrm{2}}\right)} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}\left({x}\right)}{{x}}{dx}=\frac{\pi\left(\mathrm{1}\right)^{\mathrm{1}−\mathrm{1}} }{\mathrm{2}\Gamma\left(\mathrm{1}\right)\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}\right)}=\frac{\pi}{\mathrm{2}} \\ $$$${where}\:\Gamma\left(\mathrm{1}\right)=\mathrm{1},{a}=\mathrm{1}\:{and}\:{n}=\mathrm{1} \\ $$$$\because\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}\left({x}\right)}{{x}}{dx}=\frac{\pi}{\mathrm{2}} \\ $$

Commented by mathdave last updated on 23/Sep/20

u can using IBP for d one without d symmentric bondaries

$${u}\:{can}\:{using}\:{IBP}\:{for}\:{d}\:{one}\:{without}\:{d} \\ $$$${symmentric}\:{bondaries} \\ $$

Commented by I want to learn more last updated on 23/Sep/20

Thanks sir, i appreciate.

$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate}. \\ $$

Commented by I want to learn more last updated on 23/Sep/20

I will love to see your work sir

$$\mathrm{I}\:\mathrm{will}\:\mathrm{love}\:\mathrm{to}\:\mathrm{see}\:\mathrm{your}\:\mathrm{work}\:\mathrm{sir} \\ $$

Commented by mathdave last updated on 23/Sep/20

yah it has proof

$${yah}\:{it}\:{has}\:{proof} \\ $$

Commented by I want to learn more last updated on 23/Sep/20

Please sir help me to prove it when you are less busy. Thanks sir. I appreciate.

$$\mathrm{Please}\:\mathrm{sir}\:\mathrm{help}\:\mathrm{me}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{it}\:\mathrm{when}\:\mathrm{you}\:\mathrm{are}\:\mathrm{less}\:\mathrm{busy}.\:\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$

Commented by Tawa11 last updated on 06/Sep/21

great sir

$$\mathrm{great}\:\mathrm{sir} \\ $$

Answered by Bird last updated on 24/Sep/20

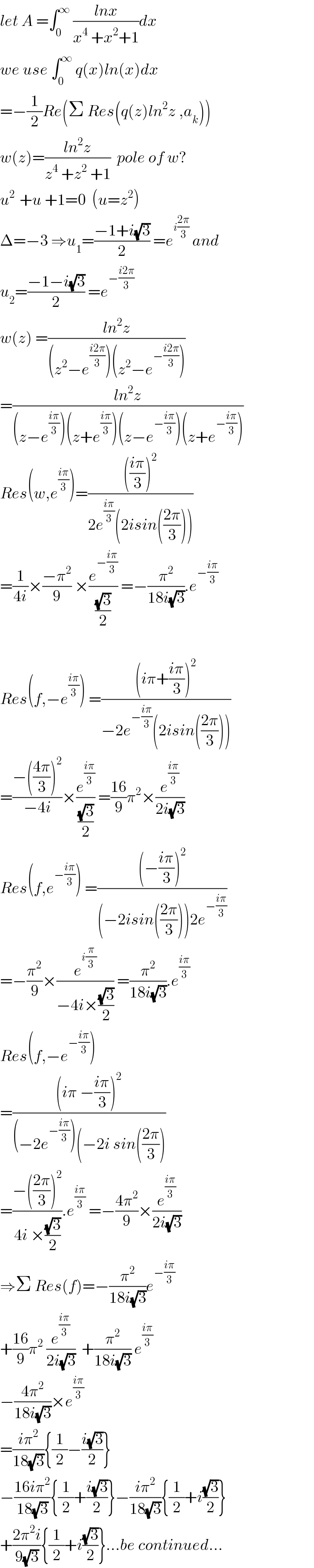
let A =∫_0 ^∞ ((lnx)/(x^4 +x^2 +1))dx we use ∫_0 ^∞ q(x)ln(x)dx =−(1/2)Re(Σ Res(q(z)ln^2 z ,a_k )) w(z)=((ln^2 z)/(z^4 +z^2 +1)) pole of w? u^(2 ) +u +1=0 (u=z^2 ) Δ=−3 ⇒u_1 =((−1+i(√3))/2) =e^(i((2π)/3)) and u_2 =((−1−i(√3))/2) =e^(−((i2π)/3)) w(z) =((ln^2 z)/((z^2 −e^((i2π)/3) )(z^2 −e^(−((i2π)/3)) ))) =((ln^2 z)/((z−e^((iπ)/3) )(z+e^((iπ)/3) )(z−e^(−((iπ)/3)) )(z+e^(−((iπ)/3)) ))) Res(w,e^((iπ)/3) )=(((((iπ)/3))^2 )/(2e^((iπ)/3) (2isin(((2π)/3))))) =(1/(4i))×((−π^2 )/9) ×(e^(−((iπ)/3)) /((√3)/2)) =−(π^2 /(18i(√3))).e^(−((iπ)/3)) Res(f,−e^((iπ)/3) ) =(((iπ+((iπ)/3))^2 )/(−2e^(−((iπ)/3)) (2isin(((2π)/3))))) =((−(((4π)/3))^2 )/(−4i))×(e^((iπ)/3) /((√3)/2)) =((16)/9)π^2 ×(e^((iπ)/3) /(2i(√3))) Res(f,e^(−((iπ)/3)) ) =(((−((iπ)/3))^2 )/((−2isin(((2π)/3)))2e^(−((iπ)/3)) )) =−(π^2 /9)×(e^(i(π/3)) /(−4i×((√3)/2))) =(π^2 /(18i(√3))).e^((iπ)/3) Res(f,−e^(−((iπ)/3)) ) =(((iπ −((iπ)/3))^2 )/((−2e^(−((iπ)/3)) )(−2i sin(((2π)/3)))) =((−(((2π)/3))^2 )/(4i ×((√3)/2))).e^((iπ)/3) =−((4π^2 )/9)×(e^((iπ)/3) /(2i(√3))) ⇒Σ Res(f)=−(π^2 /(18i(√3)))e^(−((iπ)/3)) +((16)/9)π^2 (e^((iπ)/3) /(2i(√3))) +(π^2 /(18i(√3))) e^((iπ)/3) −((4π^2 )/(18i(√3)))×e^((iπ)/3) =((iπ^2 )/(18(√3))){(1/2)−((i(√3))/2)} −((16iπ^2 )/(18(√3))){(1/2)+((i(√3))/2)}−((iπ^2 )/(18(√3))){(1/2)+i((√3)/2)} +((2π^2 i)/(9(√3))){(1/2)+i((√3)/2)}...be continued...

$${let}\:{A}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{lnx}}{{x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$${we}\:{use}\:\int_{\mathrm{0}} ^{\infty} \:{q}\left({x}\right){ln}\left({x}\right){dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}{Re}\left(\Sigma\:{Res}\left({q}\left({z}\right){ln}^{\mathrm{2}} {z}\:,{a}_{{k}} \right)\right) \\ $$$${w}\left({z}\right)=\frac{{ln}^{\mathrm{2}} {z}}{{z}^{\mathrm{4}} \:+{z}^{\mathrm{2}} \:+\mathrm{1}}\:\:{pole}\:{of}\:{w}? \\ $$$${u}^{\mathrm{2}\:} \:+{u}\:+\mathrm{1}=\mathrm{0}\:\:\left({u}={z}^{\mathrm{2}} \right) \\ $$$$\Delta=−\mathrm{3}\:\Rightarrow{u}_{\mathrm{1}} =\frac{−\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:={e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \:{and} \\ $$$${u}_{\mathrm{2}} =\frac{−\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:={e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \\ $$$${w}\left({z}\right)\:=\frac{{ln}^{\mathrm{2}} {z}}{\left({z}^{\mathrm{2}} −{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)\left({z}^{\mathrm{2}} −{e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)} \\ $$$$=\frac{{ln}^{\mathrm{2}} {z}}{\left({z}−{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}+{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)} \\ $$$${Res}\left({w},{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)=\frac{\left(\frac{{i}\pi}{\mathrm{3}}\right)^{\mathrm{2}} }{\mathrm{2}{e}^{\frac{{i}\pi}{\mathrm{3}}} \left(\mathrm{2}{isin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}{i}}×\frac{−\pi^{\mathrm{2}} }{\mathrm{9}}\:×\frac{{e}^{−\frac{{i}\pi}{\mathrm{3}}} }{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{18}{i}\sqrt{\mathrm{3}}}.{e}^{−\frac{{i}\pi}{\mathrm{3}}} \\ $$$$ \\ $$$${Res}\left({f},−{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\:=\frac{\left({i}\pi+\frac{{i}\pi}{\mathrm{3}}\right)^{\mathrm{2}} }{−\mathrm{2}{e}^{−\frac{{i}\pi}{\mathrm{3}}} \left(\mathrm{2}{isin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right)} \\ $$$$=\frac{−\left(\frac{\mathrm{4}\pi}{\mathrm{3}}\right)^{\mathrm{2}} }{−\mathrm{4}{i}}×\frac{{e}^{\frac{{i}\pi}{\mathrm{3}}} }{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\:=\frac{\mathrm{16}}{\mathrm{9}}\pi^{\mathrm{2}} ×\frac{{e}^{\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{2}{i}\sqrt{\mathrm{3}}} \\ $$$${Res}\left({f},{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\:=\frac{\left(−\frac{{i}\pi}{\mathrm{3}}\right)^{\mathrm{2}} }{\left(−\mathrm{2}{isin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right)\mathrm{2}{e}^{−\frac{{i}\pi}{\mathrm{3}}} } \\ $$$$=−\frac{\pi^{\mathrm{2}} }{\mathrm{9}}×\frac{{e}^{{i}\frac{\pi}{\mathrm{3}}} }{−\mathrm{4}{i}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{18}{i}\sqrt{\mathrm{3}}}.{e}^{\frac{{i}\pi}{\mathrm{3}}} \\ $$$${Res}\left({f},−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right) \\ $$$$=\frac{\left({i}\pi\:−\frac{{i}\pi}{\mathrm{3}}\right)^{\mathrm{2}} }{\left(−\mathrm{2}{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\left(−\mathrm{2}{i}\:{sin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right.} \\ $$$$=\frac{−\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)^{\mathrm{2}} }{\mathrm{4}{i}\:×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}.{e}^{\frac{{i}\pi}{\mathrm{3}}} \:=−\frac{\mathrm{4}\pi^{\mathrm{2}} }{\mathrm{9}}×\frac{{e}^{\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{2}{i}\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\Sigma\:{Res}\left({f}\right)=−\frac{\pi^{\mathrm{2}} }{\mathrm{18}{i}\sqrt{\mathrm{3}}}{e}^{−\frac{{i}\pi}{\mathrm{3}}} \\ $$$$+\frac{\mathrm{16}}{\mathrm{9}}\pi^{\mathrm{2}} \:\frac{{e}^{\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{2}{i}\sqrt{\mathrm{3}}}\:\:+\frac{\pi^{\mathrm{2}} }{\mathrm{18}{i}\sqrt{\mathrm{3}}}\:{e}^{\frac{{i}\pi}{\mathrm{3}}} \\ $$$$−\frac{\mathrm{4}\pi^{\mathrm{2}} }{\mathrm{18}{i}\sqrt{\mathrm{3}}}×{e}^{\frac{{i}\pi}{\mathrm{3}}} \\ $$$$=\frac{{i}\pi^{\mathrm{2}} }{\mathrm{18}\sqrt{\mathrm{3}}}\left\{\frac{\mathrm{1}}{\mathrm{2}}−\frac{{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\right\} \\ $$$$−\frac{\mathrm{16}{i}\pi^{\mathrm{2}} }{\mathrm{18}\sqrt{\mathrm{3}}}\left\{\frac{\mathrm{1}}{\mathrm{2}}+\frac{{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\right\}−\frac{{i}\pi^{\mathrm{2}} }{\mathrm{18}\sqrt{\mathrm{3}}}\left\{\frac{\mathrm{1}}{\mathrm{2}}+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right\} \\ $$$$+\frac{\mathrm{2}\pi^{\mathrm{2}} {i}}{\mathrm{9}\sqrt{\mathrm{3}}}\left\{\frac{\mathrm{1}}{\mathrm{2}}+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right\}...{be}\:{continued}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com