
Previous in Differential Equation Next in Differential Equation
Question Number 114980 by srijachakraborty last updated on 22/Sep/20

Answered by Dwaipayan Shikari last updated on 22/Sep/20
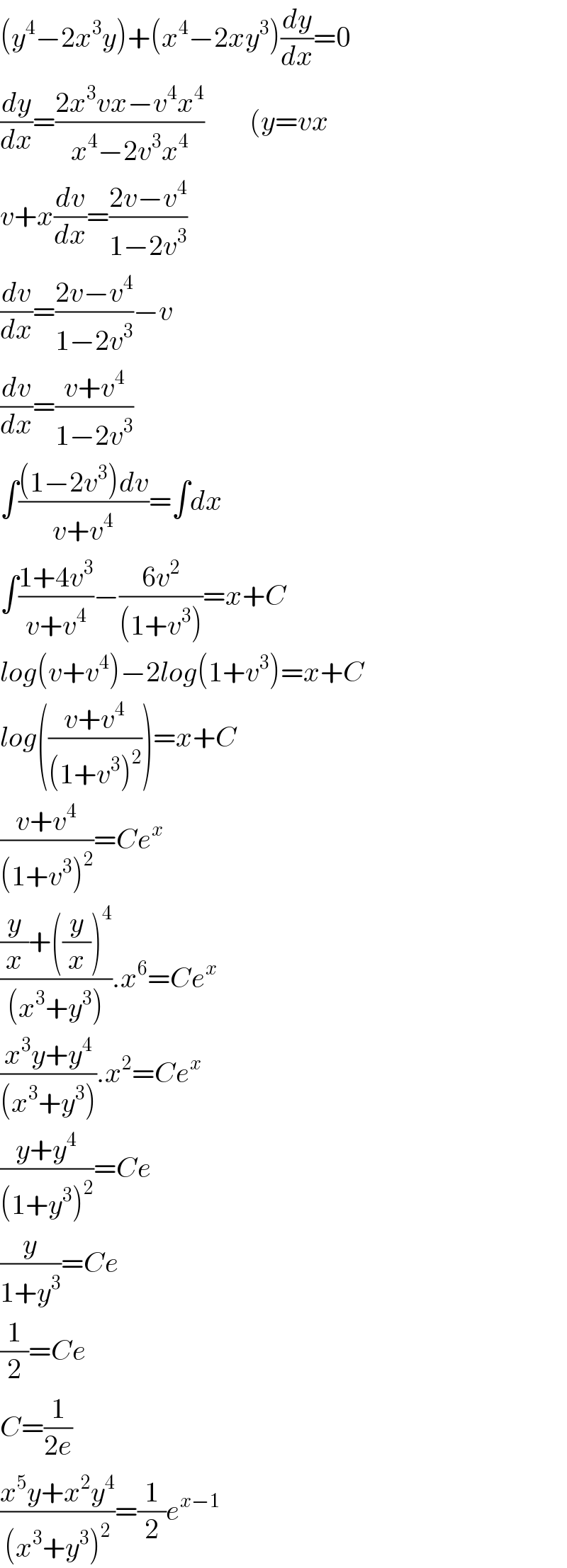
$$\left({y}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{3}} {y}\right)+\left({x}^{\mathrm{4}} −\mathrm{2}{xy}^{\mathrm{3}} \right)\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{2}{x}^{\mathrm{3}} {vx}−{v}^{\mathrm{4}} {x}^{\mathrm{4}} }{{x}^{\mathrm{4}} −\mathrm{2}{v}^{\mathrm{3}} {x}^{\mathrm{4}} }\:\:\:\:\:\:\:\:\left({y}={vx}\right. \\ $$$${v}+{x}\frac{{dv}}{{dx}}=\frac{\mathrm{2}{v}−{v}^{\mathrm{4}} }{\mathrm{1}−\mathrm{2}{v}^{\mathrm{3}} } \\ $$$$\frac{{dv}}{{dx}}=\frac{\mathrm{2}{v}−{v}^{\mathrm{4}} }{\mathrm{1}−\mathrm{2}{v}^{\mathrm{3}} }−{v} \\ $$$$\frac{{dv}}{{dx}}=\frac{{v}+{v}^{\mathrm{4}} }{\mathrm{1}−\mathrm{2}{v}^{\mathrm{3}} } \\ $$$$\int\frac{\left(\mathrm{1}−\mathrm{2}{v}^{\mathrm{3}} \right){dv}}{{v}+{v}^{\mathrm{4}} }=\int{dx} \\ $$$$\int\frac{\mathrm{1}+\mathrm{4}{v}^{\mathrm{3}} }{{v}+{v}^{\mathrm{4}} }−\frac{\mathrm{6}{v}^{\mathrm{2}} }{\left(\mathrm{1}+{v}^{\mathrm{3}} \right)}={x}+{C} \\ $$$${log}\left({v}+{v}^{\mathrm{4}} \right)−\mathrm{2}{log}\left(\mathrm{1}+{v}^{\mathrm{3}} \right)={x}+{C} \\ $$$${log}\left(\frac{{v}+{v}^{\mathrm{4}} }{\left(\mathrm{1}+{v}^{\mathrm{3}} \right)^{\mathrm{2}} }\right)={x}+{C} \\ $$$$\frac{{v}+{v}^{\mathrm{4}} }{\left(\mathrm{1}+{v}^{\mathrm{3}} \right)^{\mathrm{2}} }={Ce}^{{x}} \\ $$$$\frac{\frac{{y}}{{x}}+\left(\frac{{y}}{{x}}\right)^{\mathrm{4}} }{\left({x}^{\mathrm{3}} +{y}^{\mathrm{3}} \right)}.{x}^{\mathrm{6}} ={Ce}^{{x}} \\ $$$$\frac{{x}^{\mathrm{3}} {y}+{y}^{\mathrm{4}} }{\left({x}^{\mathrm{3}} +{y}^{\mathrm{3}} \right)}.{x}^{\mathrm{2}} ={Ce}^{{x}} \\ $$$$\frac{{y}+{y}^{\mathrm{4}} }{\left(\mathrm{1}+{y}^{\mathrm{3}} \right)^{\mathrm{2}} }={Ce} \\ $$$$\frac{{y}}{\mathrm{1}+{y}^{\mathrm{3}} }={Ce} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}={Ce} \\ $$$${C}=\frac{\mathrm{1}}{\mathrm{2}{e}} \\ $$$$\frac{{x}^{\mathrm{5}} {y}+{x}^{\mathrm{2}} {y}^{\mathrm{4}} }{\left({x}^{\mathrm{3}} +{y}^{\mathrm{3}} \right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}{e}^{{x}−\mathrm{1}} \\ $$
