
Question Number 114981 by bobhans last updated on 22/Sep/20
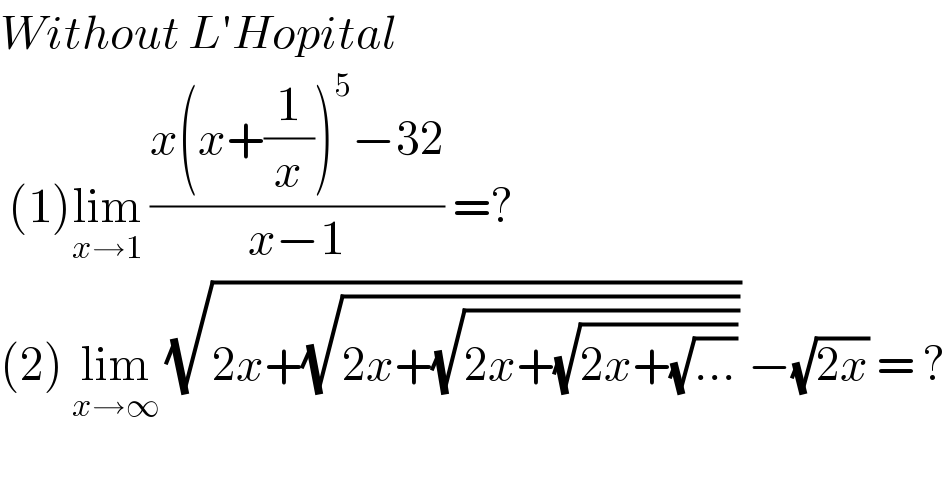
$${Without}\:{L}'{Hopital} \\ $$$$\:\left(\mathrm{1}\right)\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{x}\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{5}} −\mathrm{32}}{{x}−\mathrm{1}}\:=? \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\mathrm{2}{x}+\sqrt{\mathrm{2}{x}+\sqrt{\mathrm{2}{x}+\sqrt{\mathrm{2}{x}+\sqrt{...}}}}}\:−\sqrt{\mathrm{2}{x}}\:=\:? \\ $$
Commented by Dwaipayan Shikari last updated on 22/Sep/20
![lim_(x→1) ((x(x+(1/x))^5 −2^5 )/( (x)^(1/5) (x+(1/x))−2)).((x^(6/5) +x^(−(4/5)) −2)/(x−1)) lim_(x→1) 5.2^4 .((2/5))=32 (((x^(6/5) +x^(−(4/5)) −2)/(x−1))=(2/5)) ((a^6 +a^(−4) −2)/(a^5 −1)).((a−1)/(a−1)) (x=a^5 ) ((a^(10) +1−2a^4 )/(a^4 +a^3 +a^2 +a+1)).(1/(a^4 (a−1))) (1/5)(a^(10) +1−2a^4 ).(1/(a^5 −a^4 ))=(1/5)(a^(10) −a^8 +a^8 −2a^4 +1).(1/(a^4 (a−1)))=(1/5)(a^5 +a^4 +(((a^4 −1)^2 )/(a^4 (a−1))))=(2/5) [(((a^4 −1)(a^4 −1))/(a−1))=(((a−1)^2 (a+1)^2 (a^4 −1))/(a−1))=0]](Q114987.png)
$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{x}\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{5}} −\mathrm{2}^{\mathrm{5}} }{\:\sqrt[{\mathrm{5}}]{{x}}\left({x}+\frac{\mathrm{1}}{{x}}\right)−\mathrm{2}}.\frac{{x}^{\frac{\mathrm{6}}{\mathrm{5}}} +{x}^{−\frac{\mathrm{4}}{\mathrm{5}}} −\mathrm{2}}{{x}−\mathrm{1}} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}5}.\mathrm{2}^{\mathrm{4}} .\left(\frac{\mathrm{2}}{\mathrm{5}}\right)=\mathrm{32}\:\:\:\:\:\:\:\left(\frac{{x}^{\frac{\mathrm{6}}{\mathrm{5}}} +{x}^{−\frac{\mathrm{4}}{\mathrm{5}}} −\mathrm{2}}{{x}−\mathrm{1}}=\frac{\mathrm{2}}{\mathrm{5}}\right) \\ $$$$\frac{{a}^{\mathrm{6}} +{a}^{−\mathrm{4}} −\mathrm{2}}{{a}^{\mathrm{5}} −\mathrm{1}}.\frac{{a}−\mathrm{1}}{{a}−\mathrm{1}}\:\:\:\left({x}={a}^{\mathrm{5}} \right) \\ $$$$\frac{{a}^{\mathrm{10}} +\mathrm{1}−\mathrm{2}{a}^{\mathrm{4}} }{{a}^{\mathrm{4}} +{a}^{\mathrm{3}} +{a}^{\mathrm{2}} +{a}+\mathrm{1}}.\frac{\mathrm{1}}{{a}^{\mathrm{4}} \left({a}−\mathrm{1}\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{5}}\left({a}^{\mathrm{10}} +\mathrm{1}−\mathrm{2}{a}^{\mathrm{4}} \right).\frac{\mathrm{1}}{{a}^{\mathrm{5}} −{a}^{\mathrm{4}} }=\frac{\mathrm{1}}{\mathrm{5}}\left({a}^{\mathrm{10}} −{a}^{\mathrm{8}} +{a}^{\mathrm{8}} −\mathrm{2}{a}^{\mathrm{4}} +\mathrm{1}\right).\frac{\mathrm{1}}{{a}^{\mathrm{4}} \left({a}−\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{5}}\left({a}^{\mathrm{5}} +{a}^{\mathrm{4}} +\frac{\left({a}^{\mathrm{4}} −\mathrm{1}\right)^{\mathrm{2}} }{{a}^{\mathrm{4}} \left({a}−\mathrm{1}\right)}\right)=\frac{\mathrm{2}}{\mathrm{5}} \\ $$$$\left[\frac{\left({a}^{\mathrm{4}} −\mathrm{1}\right)\left({a}^{\mathrm{4}} −\mathrm{1}\right)}{{a}−\mathrm{1}}=\frac{\left({a}−\mathrm{1}\right)^{\mathrm{2}} \left({a}+\mathrm{1}\right)^{\mathrm{2}} \left({a}^{\mathrm{4}} −\mathrm{1}\right)}{{a}−\mathrm{1}}=\mathrm{0}\right] \\ $$$$ \\ $$
Commented by bemath last updated on 23/Sep/20
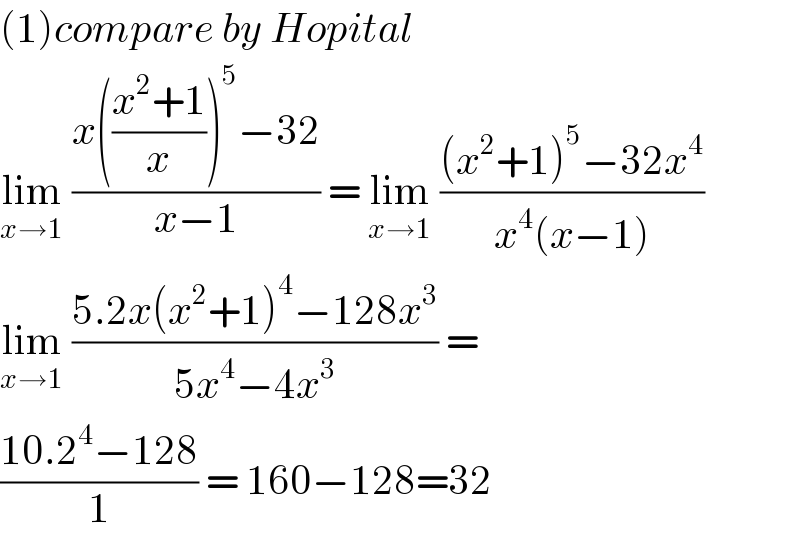
$$\left(\mathrm{1}\right){compare}\:{by}\:{Hopital} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{x}\left(\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}}\right)^{\mathrm{5}} −\mathrm{32}}{{x}−\mathrm{1}}\:=\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{5}} −\mathrm{32}{x}^{\mathrm{4}} }{{x}^{\mathrm{4}} \left({x}−\mathrm{1}\right)} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{5}.\mathrm{2}{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{4}} −\mathrm{128}{x}^{\mathrm{3}} }{\mathrm{5}{x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{3}} }\:= \\ $$$$\frac{\mathrm{10}.\mathrm{2}^{\mathrm{4}} −\mathrm{128}}{\mathrm{1}}\:=\:\mathrm{160}−\mathrm{128}=\mathrm{32} \\ $$
Answered by john santu last updated on 22/Sep/20
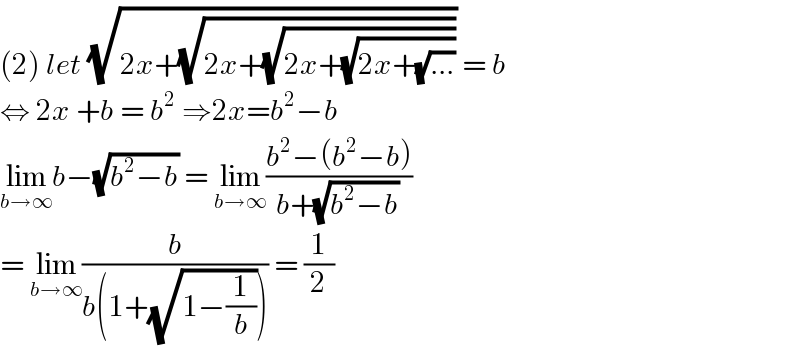
$$\left(\mathrm{2}\right)\:{let}\:\sqrt{\mathrm{2}{x}+\sqrt{\mathrm{2}{x}+\sqrt{\mathrm{2}{x}+\sqrt{\mathrm{2}{x}+\sqrt{...}}}}}\:=\:{b} \\ $$$$\Leftrightarrow\:\mathrm{2}{x}\:+{b}\:=\:{b}^{\mathrm{2}} \:\Rightarrow\mathrm{2}{x}={b}^{\mathrm{2}} −{b} \\ $$$$\underset{{b}\rightarrow\infty} {\mathrm{lim}}{b}−\sqrt{{b}^{\mathrm{2}} −{b}}\:=\:\underset{{b}\rightarrow\infty} {\mathrm{lim}}\frac{{b}^{\mathrm{2}} −\left({b}^{\mathrm{2}} −{b}\right)}{{b}+\sqrt{{b}^{\mathrm{2}} −{b}}} \\ $$$$=\:\underset{{b}\rightarrow\infty} {\mathrm{lim}}\frac{{b}}{{b}\left(\mathrm{1}+\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{b}}}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by Dwaipayan Shikari last updated on 22/Sep/20
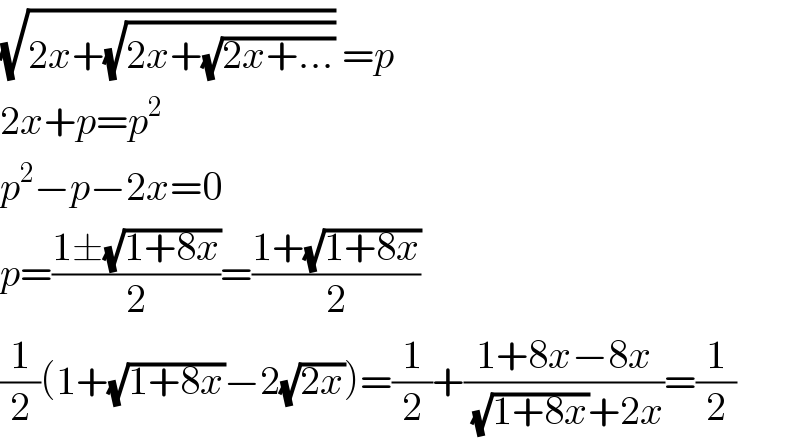
$$\sqrt{\mathrm{2}{x}+\sqrt{\mathrm{2}{x}+\sqrt{\mathrm{2}{x}+...}}}\:={p} \\ $$$$\mathrm{2}{x}+{p}={p}^{\mathrm{2}} \\ $$$${p}^{\mathrm{2}} −{p}−\mathrm{2}{x}=\mathrm{0} \\ $$$${p}=\frac{\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{8}{x}}}{\mathrm{2}}=\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{8}{x}}}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{8}{x}}−\mathrm{2}\sqrt{\mathrm{2}{x}}\right)=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}+\mathrm{8}{x}−\mathrm{8}{x}}{\:\sqrt{\mathrm{1}+\mathrm{8}{x}}+\mathrm{2}{x}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
