
Question Number 11500 by @ANTARES_VY last updated on 27/Mar/17

$$\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{x}}−\mathrm{4}\right)\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{x}}+\mathrm{4}\right)=\mathrm{9} \\ $$$$\boldsymbol{\mathrm{find}}\:\:\boldsymbol{\mathrm{the}}\:\:\boldsymbol{\mathrm{equation}}\:\:\boldsymbol{\mathrm{has}}\:\:\boldsymbol{\mathrm{multiple}}\:\:\boldsymbol{\mathrm{roots}}. \\ $$
Answered by ridwan balatif last updated on 27/Mar/17
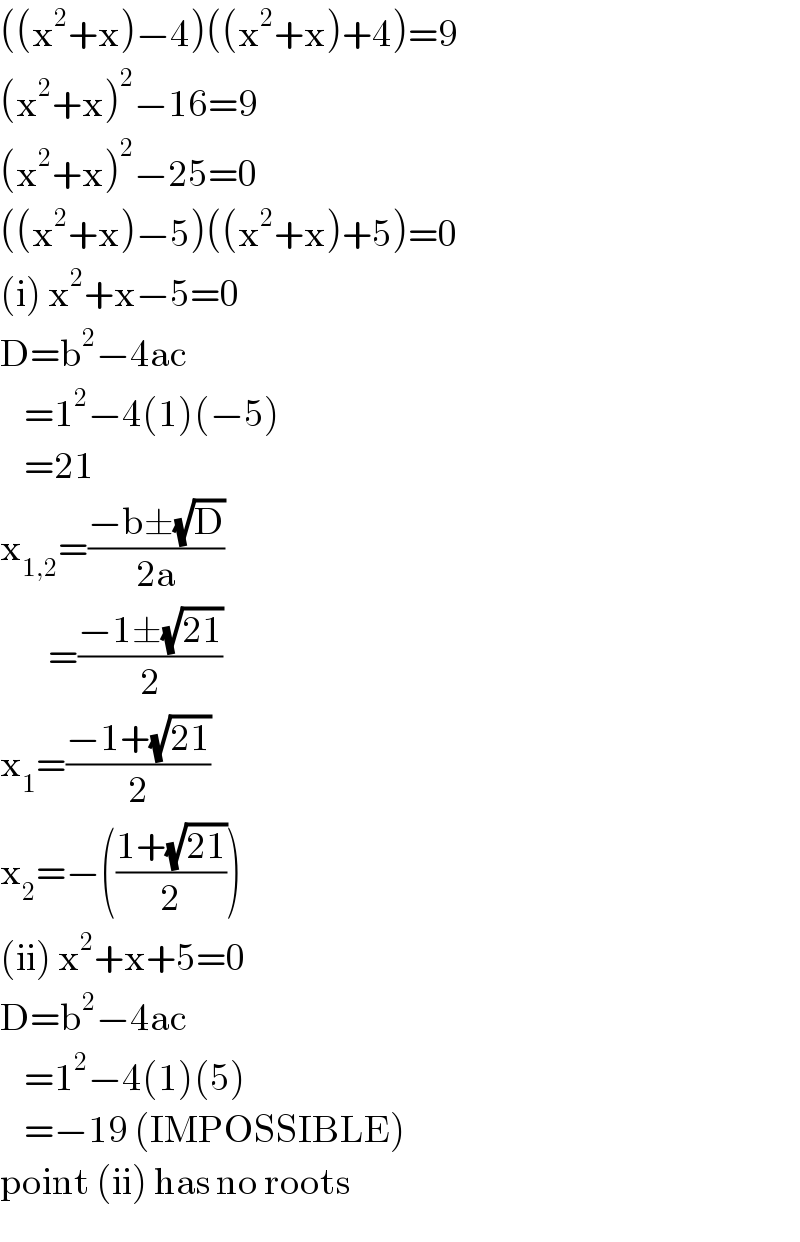
$$\left(\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)−\mathrm{4}\right)\left(\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)+\mathrm{4}\right)=\mathrm{9} \\ $$$$\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)^{\mathrm{2}} −\mathrm{16}=\mathrm{9} \\ $$$$\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)^{\mathrm{2}} −\mathrm{25}=\mathrm{0} \\ $$$$\left(\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)−\mathrm{5}\right)\left(\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)+\mathrm{5}\right)=\mathrm{0} \\ $$$$\left(\mathrm{i}\right)\:\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{5}=\mathrm{0} \\ $$$$\mathrm{D}=\mathrm{b}^{\mathrm{2}} −\mathrm{4ac} \\ $$$$\:\:\:\:=\mathrm{1}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}\right)\left(−\mathrm{5}\right) \\ $$$$\:\:\:\:=\mathrm{21} \\ $$$$\mathrm{x}_{\mathrm{1},\mathrm{2}} =\frac{−\mathrm{b}\pm\sqrt{\mathrm{D}}}{\mathrm{2a}} \\ $$$$\:\:\:\:\:\:\:\:=\frac{−\mathrm{1}\pm\sqrt{\mathrm{21}}}{\mathrm{2}} \\ $$$$\mathrm{x}_{\mathrm{1}} =\frac{−\mathrm{1}+\sqrt{\mathrm{21}}}{\mathrm{2}} \\ $$$$\mathrm{x}_{\mathrm{2}} =−\left(\frac{\mathrm{1}+\sqrt{\mathrm{21}}}{\mathrm{2}}\right) \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{5}=\mathrm{0} \\ $$$$\mathrm{D}=\mathrm{b}^{\mathrm{2}} −\mathrm{4ac} \\ $$$$\:\:\:\:=\mathrm{1}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}\right)\left(\mathrm{5}\right) \\ $$$$\:\:\:\:=−\mathrm{19}\:\left(\mathrm{IMPOSSIBLE}\right) \\ $$$$\mathrm{point}\:\left(\mathrm{ii}\right)\:\mathrm{has}\:\mathrm{no}\:\mathrm{roots} \\ $$
Commented by @ANTARES_VY last updated on 27/Mar/17

$$\boldsymbol{\mathrm{The}}\:\:\boldsymbol{\mathrm{answer}}\:\:\boldsymbol{\mathrm{is}}:\:−\mathrm{5}. \\ $$
Commented by @ANTARES_VY last updated on 27/Mar/17

$$\boldsymbol{\mathrm{error}} \\ $$
Commented by mrW1 last updated on 27/Mar/17

$${please}\:{explain}\:{what}\:{you}\:{mean}\:{with} \\ $$$${your}\:{question}. \\ $$
Commented by mrW1 last updated on 27/Mar/17

$${then}\:{your}\:{question}\:{should}\:{be}:\:{find}\:{the} \\ $$$${product}\:{of}\:{the}\:{real}\:{roots}\:{of}\:{the} \\ $$$${equation}. \\ $$
Commented by @ANTARES_VY last updated on 27/Mar/17

$$\boldsymbol{\mathrm{x}}_{\mathrm{1}} ×\boldsymbol{\mathrm{x}}_{\mathrm{2}} =? \\ $$
Commented by mrW1 last updated on 27/Mar/17

$${yes}.\:\:{x}_{\mathrm{1}} ×{x}_{\mathrm{2}} =−\mathrm{5} \\ $$
Commented by sandy_suhendra last updated on 27/Mar/17

$$\mathrm{from}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{of}\:\mathrm{Mr}\:\mathrm{Ridwan}\:\mathrm{Balatif} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{5}=\mathrm{0}\:\mathrm{has}\:\mathrm{2}\:\mathrm{imaginary}\:\mathrm{roots}\:\mathrm{because}\:\mathrm{D}<\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{5}=\mathrm{0}\:\mathrm{has}\:\mathrm{2}\:\mathrm{real}\:\mathrm{roots}\:\mathrm{x}_{\mathrm{1}} \:\mathrm{and}\:\mathrm{x}_{\mathrm{2}} \:\mathrm{because}\:\mathrm{D}>\mathrm{0}\:\:\:\:\: \\ $$$$\mathrm{so}\:\mathrm{x}_{\mathrm{1}} .\mathrm{x}_{\mathrm{2}} \:=\:\frac{\mathrm{c}}{\mathrm{a}}\:=\:\frac{−\mathrm{5}}{\mathrm{1}}\:=\:−\mathrm{5} \\ $$
Answered by ajfour last updated on 27/Mar/17

$$\mathrm{x}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}\pm\mathrm{20}}}{\mathrm{2}}\:. \\ $$
