∫_C (e^z /(1−cos z))dz ; C:∣z∣=1


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 115009 by arcana last updated on 22/Sep/20

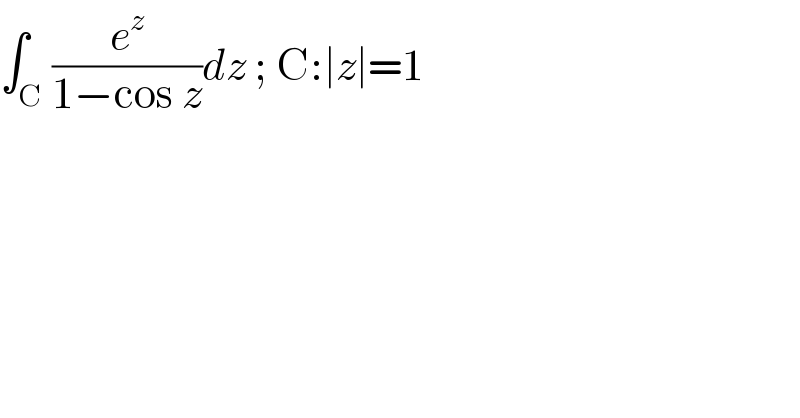
$\int_{C} \frac{e^{z}}{1 - \cos z} d z; C :∣ z ∣= 1$
	Answered by Olaf last updated on 24/Sep/20

	$\int_{C} \frac{co z + i \sin z}{1 - \cos z} d z$ $\int_{C} \frac{1 + i \sin z + (\cos z - 1)}{1 - \cos z} d z$ $\int_{C} \frac{d z}{1 - \cos z} + i \int_{C} \frac{\sin z}{1 - \cos z} - \int_{C} d z$ $\int_{C} \frac{2 d z}{\sin^{2} \frac{z}{2}} + i \int_{C} \frac{\sin z}{1 - \cos z} - \int_{C} d z$ ${[- 4 \cot \frac{z}{2} + i \ln (1 - \cos z) - z]}_{C}$ $Let z = e^{i θ}, θ \in [0; 2 π]$ ${[- 4 \cot \frac{e^{i θ}}{2} + i \ln (1 - \cos e^{i θ}) - e^{i θ}]}_{0}^{2 π}$ $= 0$
	Answered by Bird last updated on 24/Sep/20
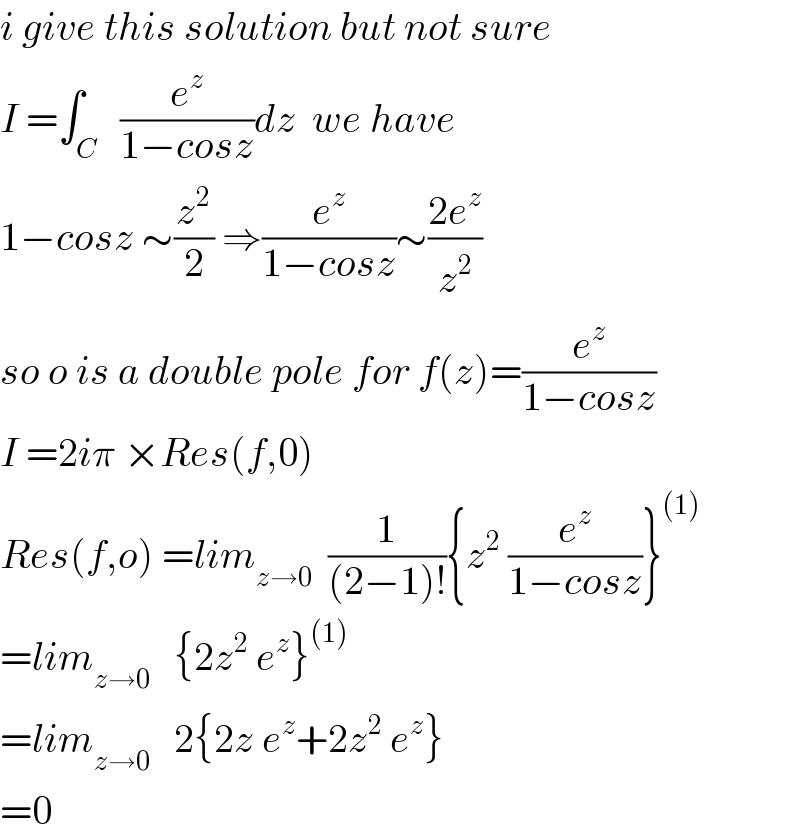
	$i give this solution but not sure I =∫_C (e^z /(1−cosz))dz we have 1−cosz ∼(z^2 /2) ⇒(e^z /(1−cosz))∼((2e^z )/z^2 ) so o is a double pole for f(z)=(e^z /(1−cosz)) I =2iπ ×Res(f,0) Res(f,o) =lim_(z→0) (1/((2−1)!)){z^2 (e^z /(1−cosz))}^((1)) =lim_(z→0) {2z^2 e^z }^((1)) =lim_(z→0) 2{2z e^z +2z^2 e^z } =0$
	$i g i v e t h i s s o l u t i o n b u t n o t s u r e$ $I = \int_{C} \frac{e^{z}}{1 - c o s z} d z w e h a v e$ $1 - c o s z \sim \frac{z^{2}}{2} \Rightarrow \frac{e^{z}}{1 - c o s z} \sim \frac{2 e^{z}}{z^{2}}$ $s o o i s a d o u b l e p o l e f o r f (z) = \frac{e^{z}}{1 - c o s z}$ $I = 2 i π \times R e s (f, 0)$ $R e s (f, o) = {l i m}_{z \to 0} \frac{1}{(2 - 1)!} {z^{2} \frac{e^{z}}{1 - c o s z}}^{(1)}$ $= {l i m}_{z \to 0} {2 z^{2} e^{z}}^{(1)}$ $= {l i m}_{z \to 0} 2 {2 z e^{z} + 2 z^{2} e^{z}}$ $= 0$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum