Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 11501 by @ANTARES_VY last updated on 27/Mar/17

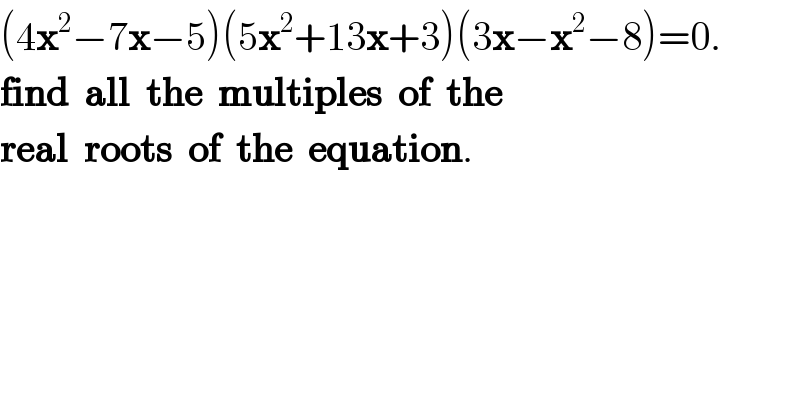
(4x^2 −7x−5)(5x^2 +13x+3)(3x−x^2 −8)=0. find all the multiples of the real roots of the equation.

$$\left(\mathrm{4}\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{7}\boldsymbol{\mathrm{x}}−\mathrm{5}\right)\left(\mathrm{5}\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{13}\boldsymbol{\mathrm{x}}+\mathrm{3}\right)\left(\mathrm{3}\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{8}\right)=\mathrm{0}. \\ $$$$\boldsymbol{\mathrm{find}}\:\:\boldsymbol{\mathrm{all}}\:\:\boldsymbol{\mathrm{the}}\:\:\boldsymbol{\mathrm{multiples}}\:\:\boldsymbol{\mathrm{of}}\:\:\boldsymbol{\mathrm{the}} \\ $$$$\boldsymbol{\mathrm{real}}\:\:\boldsymbol{\mathrm{roots}}\:\:\boldsymbol{\mathrm{of}}\:\:\boldsymbol{\mathrm{the}}\:\:\boldsymbol{\mathrm{equation}}. \\ $$

Commented by mrW1 last updated on 27/Mar/17

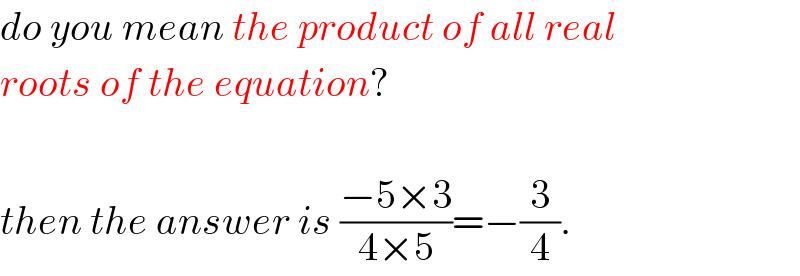
do you mean the product of all real roots of the equation? then the answer is ((−5×3)/(4×5))=−(3/4).

$${do}\:{you}\:{mean}\:{the}\:{product}\:{of}\:{all}\:{real} \\ $$$${roots}\:{of}\:{the}\:{equation}? \\ $$$$ \\ $$$${then}\:{the}\:{answer}\:{is}\:\frac{−\mathrm{5}×\mathrm{3}}{\mathrm{4}×\mathrm{5}}=−\frac{\mathrm{3}}{\mathrm{4}}. \\ $$

Answered by Joel576 last updated on 27/Mar/17

• 4x^2 − 7x − 5 = 0 x_(1,2) = ((7 ± (√(49 − (4.4.−5))))/(2.4)) = ((7 ± (√(129)))/8) x_1 = ((7 + (√(129)))/8) x_2 = ((7 − (√(129)))/8) • 5x^2 + 13x + 3 = 0 x_(3,4) = ((−13 ± (√(169 − (4.5.3))))/(2.5)) = ((−13 ± (√(109)))/(10)) x_3 = ((−13 + (√(109)))/(10)) x_4 = ((−13 − (√(109)))/(10)) • −x^2 + 3x − 8 = 0 x_(5,6) = ((−3 ± (√(9 − (4.−1.−8))))/(2.−1)) = ((−3 ± (√(−23)))/(−2)) → imaginary (((7 + (√(129)))/8) . ((7 − (√(129)))/8)) (((−13 + (√(109)))/(10)) . ((−13 − (√(109)))/(10))) = (((49 − 129)/(64)))(((169 − 109)/(100))) = −(3/4)

$$\bullet\:\mathrm{4}{x}^{\mathrm{2}} \:−\:\mathrm{7}{x}\:−\:\mathrm{5}\:=\:\mathrm{0} \\ $$$$\:\:\:\:{x}_{\mathrm{1},\mathrm{2}} \:=\:\frac{\mathrm{7}\:\pm\:\sqrt{\mathrm{49}\:−\:\left(\mathrm{4}.\mathrm{4}.−\mathrm{5}\right)}}{\mathrm{2}.\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{7}\:\pm\:\sqrt{\mathrm{129}}}{\mathrm{8}} \\ $$$$\:\:\:\:{x}_{\mathrm{1}} \:=\:\frac{\mathrm{7}\:+\:\sqrt{\mathrm{129}}}{\mathrm{8}} \\ $$$$\:\:\:\:{x}_{\mathrm{2}} \:=\:\frac{\mathrm{7}\:−\:\sqrt{\mathrm{129}}}{\mathrm{8}} \\ $$$$\bullet\:\mathrm{5}{x}^{\mathrm{2}} \:+\:\mathrm{13}{x}\:+\:\mathrm{3}\:=\:\mathrm{0} \\ $$$$\:\:\:\:{x}_{\mathrm{3},\mathrm{4}} \:=\:\frac{−\mathrm{13}\:\pm\:\sqrt{\mathrm{169}\:−\:\left(\mathrm{4}.\mathrm{5}.\mathrm{3}\right)}}{\mathrm{2}.\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{−\mathrm{13}\:\pm\:\sqrt{\mathrm{109}}}{\mathrm{10}} \\ $$$$\:\:\:\:\:{x}_{\mathrm{3}} \:=\:\frac{−\mathrm{13}\:+\:\sqrt{\mathrm{109}}}{\mathrm{10}} \\ $$$$\:\:\:\:\:{x}_{\mathrm{4}} \:=\:\frac{−\mathrm{13}\:−\:\sqrt{\mathrm{109}}}{\mathrm{10}} \\ $$$$\bullet\:−{x}^{\mathrm{2}} \:+\:\mathrm{3}{x}\:−\:\mathrm{8}\:=\:\mathrm{0} \\ $$$$\:\:\:\:{x}_{\mathrm{5},\mathrm{6}} \:=\:\frac{−\mathrm{3}\:\pm\:\sqrt{\mathrm{9}\:−\:\left(\mathrm{4}.−\mathrm{1}.−\mathrm{8}\right)}}{\mathrm{2}.−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{−\mathrm{3}\:\pm\:\sqrt{−\mathrm{23}}}{−\mathrm{2}}\:\:\rightarrow\:\mathrm{imaginary} \\ $$$$\: \\ $$$$\left(\frac{\mathrm{7}\:+\:\sqrt{\mathrm{129}}}{\mathrm{8}}\:.\:\frac{\mathrm{7}\:−\:\sqrt{\mathrm{129}}}{\mathrm{8}}\right)\:\left(\frac{−\mathrm{13}\:+\:\sqrt{\mathrm{109}}}{\mathrm{10}}\:.\:\frac{−\mathrm{13}\:−\:\sqrt{\mathrm{109}}}{\mathrm{10}}\right) \\ $$$$=\:\left(\frac{\mathrm{49}\:−\:\mathrm{129}}{\mathrm{64}}\right)\left(\frac{\mathrm{169}\:−\:\mathrm{109}}{\mathrm{100}}\right) \\ $$$$=\:−\frac{\mathrm{3}}{\mathrm{4}} \\ $$

Commented by @ANTARES_VY last updated on 27/Mar/17

error

$$\boldsymbol{\mathrm{error}} \\ $$

Answered by sandy_suhendra last updated on 27/Mar/17

I′ve made a mistake, so I corrected 4x^2 −7x−5=0 has 2 real roots x_1 and x_(2 ) because D>0 5x^2 +13x+3=0 has 2 real roots x_3 and x_4 because D>0 3x−x^2 −8=0 has 2 imaginary roots because D<0 so (4x^2 −7x−5)(5x^2 +13x+3)=0 has 4 real roots coefisien of x^4 =a coefisien of x^3 =b coefisien of x^2 =c coefisien of x^ =d constant = e so e=−5×3=−15 a = 4×5=20 x_1 .x_2 .x_3 .x_4 =(e/a)=((−15)/(20))=− (3/4)

$$\mathrm{I}'\mathrm{ve}\:\mathrm{made}\:\mathrm{a}\:\mathrm{mistake},\:\mathrm{so}\:\mathrm{I}\:\mathrm{corrected} \\ $$$$\mathrm{4x}^{\mathrm{2}} −\mathrm{7x}−\mathrm{5}=\mathrm{0}\:\mathrm{has}\:\mathrm{2}\:\mathrm{real}\:\mathrm{roots}\:\mathrm{x}_{\mathrm{1}} \:\mathrm{and}\:\mathrm{x}_{\mathrm{2}\:} \mathrm{because}\:\mathrm{D}>\mathrm{0} \\ $$$$\mathrm{5x}^{\mathrm{2}} +\mathrm{13x}+\mathrm{3}=\mathrm{0}\:\mathrm{has}\:\mathrm{2}\:\mathrm{real}\:\mathrm{roots}\:\mathrm{x}_{\mathrm{3}} \:\mathrm{and}\:\mathrm{x}_{\mathrm{4}} \:\mathrm{because}\:\mathrm{D}>\mathrm{0}\:\:\:\:\:\: \\ $$$$\mathrm{3x}−\mathrm{x}^{\mathrm{2}} −\mathrm{8}=\mathrm{0}\:\mathrm{has}\:\mathrm{2}\:\mathrm{imaginary}\:\mathrm{roots}\:\mathrm{because}\:\mathrm{D}<\mathrm{0} \\ $$$$\mathrm{so}\:\left(\mathrm{4x}^{\mathrm{2}} −\mathrm{7x}−\mathrm{5}\right)\left(\mathrm{5x}^{\mathrm{2}} +\mathrm{13x}+\mathrm{3}\right)=\mathrm{0}\:\mathrm{has}\:\mathrm{4}\:\mathrm{real}\:\mathrm{roots}\:\:\:\:\: \\ $$$$\mathrm{coefisien}\:\mathrm{of}\:\mathrm{x}^{\mathrm{4}} =\mathrm{a} \\ $$$$\mathrm{coefisien}\:\mathrm{of}\:\mathrm{x}^{\mathrm{3}} =\mathrm{b} \\ $$$$\mathrm{coefisien}\:\mathrm{of}\:\mathrm{x}^{\mathrm{2}} =\mathrm{c} \\ $$$$\mathrm{coefisien}\:\mathrm{of}\:\mathrm{x}^{} =\mathrm{d} \\ $$$$\mathrm{constant}\:=\:\mathrm{e} \\ $$$$\mathrm{so}\:\mathrm{e}=−\mathrm{5}×\mathrm{3}=−\mathrm{15} \\ $$$$\:\:\:\:\:\mathrm{a}\:=\:\mathrm{4}×\mathrm{5}=\mathrm{20} \\ $$$$\mathrm{x}_{\mathrm{1}} .\mathrm{x}_{\mathrm{2}} .\mathrm{x}_{\mathrm{3}} .\mathrm{x}_{\mathrm{4}} =\frac{\mathrm{e}}{\mathrm{a}}=\frac{−\mathrm{15}}{\mathrm{20}}=−\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$

Answered by ajfour last updated on 27/Mar/17

(3/4)n where n belongs to integers.

$$\frac{\mathrm{3}}{\mathrm{4}}\mathrm{n}\:\:\mathrm{where}\:\mathrm{n}\:\mathrm{belongs}\:\mathrm{to}\:\mathrm{integers}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com