Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 115014 by mathdave last updated on 23/Sep/20

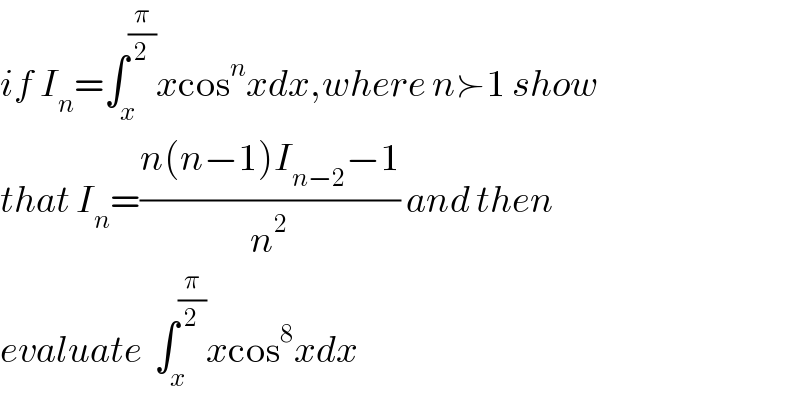
$$if{I}_n={\int }_x^{\frac{\pi }{2}}x{\cos }^{n}xdx,wheren\succ 1show$$$$that{I}_n=\frac{n(n-1)I_{n-2}-1}{n^2}andthen$$$$evaluate{\int }_x^{\frac{\pi }{2}}x{\cos }^{8}xdx$$

Answered by Olaf last updated on 23/Sep/20

$$$$$${\mathrm{I}}_n={\int }_0^{\frac{\pi }{2}}x{\cos }^{n}xdx$$$${\mathrm{I}}_n-{\mathrm{I}}_{n+2}={\int }_0^{\frac{\pi }{2}}x{\cos }^{n}x(1-{\cos }^{2}x)dx$$$${\mathrm{I}}_n-{\mathrm{I}}_{n+2}=-{\int }_0^{\frac{\pi }{2}}\left(x\sin x\right)(-\sin x{\cos }^{n}x)dx$$$${\mathrm{I}}_n-{\mathrm{I}}_{n+2}=-{\left[x\sin x\frac{{\cos }^{n+1}x}{n+1}\right]}_0^{\frac{\pi }{2}}$$$$+{\int }_0^{\frac{\pi }{2}}(\sin x+x\cos x)\frac{{\cos }^{n+1}x}{n+1}dx$$$${\mathrm{I}}_n-{\mathrm{I}}_{n+2}=-{\int }_0^{\frac{\pi }{2}}(-\sin x\frac{{\cos }^{n+1}x}{n+1})dx$$$$+\frac{1}{n+1}{\mathrm{I}}_{n+2}$$$${\mathrm{I}}_n-{\mathrm{I}}_{n+2}=-{\left[\frac{{\cos }^{n+2}x}{(n+1)(n+2)}\right]}_0^{\frac{\pi }{2}}+\frac{1}{n+1}{\mathrm{I}}_{n+2}$$$${\mathrm{I}}_n=\frac{1}{(n+1)(n+2)}+{\mathrm{I}}_{n+2}+\frac{1}{n+1}{\mathrm{I}}_{n+2}$$$${\mathrm{I}}_n=\frac{n+2}{n+1}{\mathrm{I}}_{n+2}+\frac{1}{(n+1)(n+2)}$$$${\mathrm{I}}_{n+2}=\frac{n+1}{n+2}{\mathrm{I}}_n-\frac{1}{{(n+2)}^2}\left(1\right)$$$${\mathrm{I}}_n=\frac{n(n-1){\mathrm{I}}_{n-2}-1}{n^2}$$$${\mathrm{I}}_0={\int }_0^{\frac{\pi }{2}}xdx={\left[\frac{x^2}{2}\right]}_0^{\frac{\pi }{2}}=\frac{{\pi }^2}{8}$$$$\mathrm{With}\left(1\right):{\mathrm{I}}_2=\frac{1}{2}\left(\frac{{\pi }^2}{8}\right)-\frac{1}{4}=\frac{{\pi }^2}{16}-\frac{1}{4}$$$${\mathrm{I}}_4=\frac{3}{4}(\frac{{\pi }^2}{16}-\frac{1}{4})-\frac{1}{16}=\frac{3{\pi }^2}{64}-\frac{1}{4}$$$${\mathrm{I}}_6=\frac{5}{6}(\frac{3{\pi }^2}{64}-\frac{1}{4})-\frac{1}{36}=\frac{5{\pi }^2}{128}-\frac{17}{72}$$$${\mathrm{I}}_8=\frac{7}{8}(\frac{5{\pi }^2}{128}-\frac{17}{72})-\frac{1}{64}=\frac{35{\pi }^2}{1024}-\frac{2}{9}$$$${\mathrm{I}}_8={\int }_0^{\frac{\pi }{2}}x{\cos }^{8}xdx=\frac{35{\pi }^2}{1024}-\frac{2}{9}$$

Commented by Tawa11 last updated on 06/Sep/21

$$\mathrm{great}\mathrm{sir}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com