
Question Number 115030 by bobhans last updated on 23/Sep/20
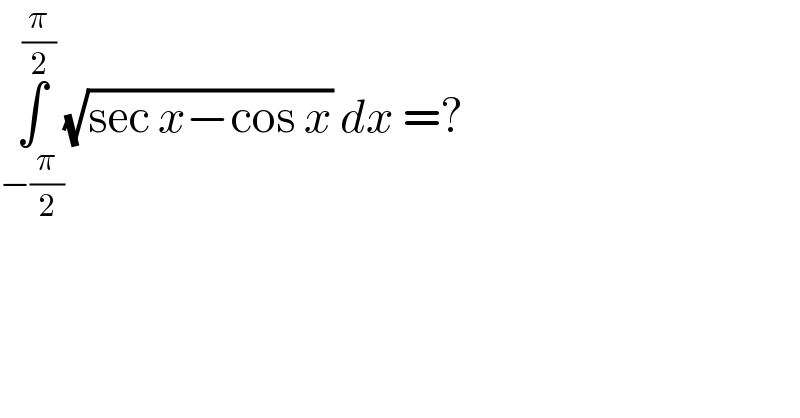
$$\underset{−\frac{\pi}{\mathrm{2}}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\sqrt{\mathrm{sec}\:{x}−\mathrm{cos}\:{x}}\:{dx}\:=? \\ $$
Answered by bemath last updated on 23/Sep/20
![∫_(−(π/2)) ^(π/2) (√((1−cos^2 x)/(cos x))) dx = ∫_(−(π/2)) ^(π/2) ((∣sin x∣)/( (√(cos x)))) dx = −∫_(−(π/2)) ^0 ((sin x)/( (√(cos x)))) dx + ∫_0 ^(π/2) ((sin x)/( (√(cos x)))) dx = ∫_(−(π/2)) ^0 ((d(cos x))/( (√(cos x)))) −∫_0 ^(π/2) ((d(cos x))/( (√(cos x)))) = 2 [ (√(cos x )) ]_(−(π/2)) ^( 0) −2 [ (√(cos x )) ] _0^(π/2) = 2 −2(0−1) = 4](Q115032.png)
$$\underset{−\frac{\pi}{\mathrm{2}}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\sqrt{\frac{\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} {x}}{\mathrm{cos}\:{x}}}\:{dx}\:=\:\underset{−\frac{\pi}{\mathrm{2}}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{\mid\mathrm{sin}\:{x}\mid}{\:\sqrt{\mathrm{cos}\:{x}}}\:{dx} \\ $$$$=\:−\underset{−\frac{\pi}{\mathrm{2}}} {\overset{\mathrm{0}} {\int}}\frac{\mathrm{sin}\:{x}}{\:\sqrt{\mathrm{cos}\:{x}}}\:{dx}\:+\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{\mathrm{sin}\:{x}}{\:\sqrt{\mathrm{cos}\:{x}}}\:{dx}\: \\ $$$$=\:\underset{−\frac{\pi}{\mathrm{2}}} {\overset{\mathrm{0}} {\int}}\frac{{d}\left(\mathrm{cos}\:{x}\right)}{\:\sqrt{\mathrm{cos}\:{x}}}\:−\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{{d}\left(\mathrm{cos}\:{x}\right)}{\:\sqrt{\mathrm{cos}\:{x}}} \\ $$$$=\:\mathrm{2}\:\left[\:\sqrt{\mathrm{cos}\:{x}\:}\:\right]_{−\frac{\pi}{\mathrm{2}}} ^{\:\:\:\mathrm{0}} \:\:−\mathrm{2}\:\left[\:\sqrt{\mathrm{cos}\:{x}\:}\:\right]\:_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\:\mathrm{2}\:−\mathrm{2}\left(\mathrm{0}−\mathrm{1}\right)\:=\:\mathrm{4} \\ $$
Answered by mathmax by abdo last updated on 23/Sep/20
![A =∫_(−(π/2)) ^(π/2) (√((1/(cosx))−cosx))dx ⇒A =2∫_0 ^(π/2) (√((1−cos^2 x)/(cosx)))dx =2 ∫_0 ^(π/2) ((∣sinx∣)/(√(cosx)))dx =2 ∫_0 ^(π/2) ((sinx)/(√(cosx)))dx =2[−2(√(cosx))]_0 ^(π/2) =2{2} =4](Q115088.png)
$$\mathrm{A}\:=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\frac{\mathrm{1}}{\mathrm{cosx}}−\mathrm{cosx}}\mathrm{dx}\:\:\Rightarrow\mathrm{A}\:=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\frac{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{cosx}}}\mathrm{dx} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mid\mathrm{sinx}\mid}{\sqrt{\mathrm{cosx}}}\mathrm{dx}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{sinx}}{\sqrt{\mathrm{cosx}}}\mathrm{dx}\:=\mathrm{2}\left[−\mathrm{2}\sqrt{\mathrm{cosx}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\mathrm{2}\left\{\mathrm{2}\right\}\:=\mathrm{4} \\ $$
