
Question Number 115033 by bobhans last updated on 23/Sep/20
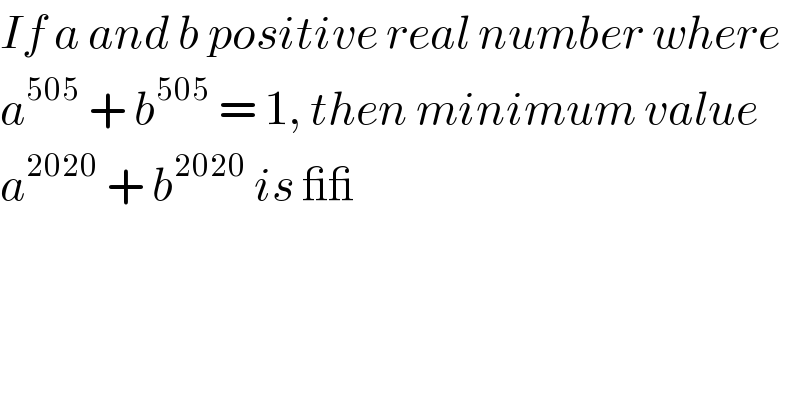
$${If}\:{a}\:{and}\:{b}\:{positive}\:{real}\:{number}\:{where} \\ $$$${a}^{\mathrm{505}} \:+\:{b}^{\mathrm{505}} \:=\:\mathrm{1},\:{then}\:{minimum}\:{value} \\ $$$${a}^{\mathrm{2020}} \:+\:{b}^{\mathrm{2020}} \:{is}\:\_\_ \\ $$
Answered by 1549442205PVT last updated on 23/Sep/20
![Put a^(505) =x,b^(505) =y⇒x+y=1.We need find minimum value of P=x^4 +y^4 Since x,y>0,1=x+y=((√x)−(√y))^2 +2(√(xy))≥2(√(xy)) ⇒(√(xy))≤1/2⇒xy≤1/4(1).Hence, x^4 +y^4 =(x+y)^4 −4xy(x^2 +y^4 )−6x^2 y^2 =1−4xy[(x+y)^2 −2xy]−6x^2 y^2 =1−4xy(1−2xy)−6(xy)^2 =1−4xy+2(xy)^2 =2(xy−(1/4))^2 −3xy+(7/8)≥0−3.(1/4)+(7/8) =(1/8).The equality ocurrs if and only if x=y=1/2⇔a=b=^(505) (√(1/2)) Thus (a^(2020) +b^(2020) )_(min) =(1/8) when a=b=(1/( ^(505) (√2)))](Q115044.png)
$$\mathrm{Put}\:\mathrm{a}^{\mathrm{505}} =\mathrm{x},\mathrm{b}^{\mathrm{505}} =\mathrm{y}\Rightarrow\mathrm{x}+\mathrm{y}=\mathrm{1}.\mathrm{We}\:\mathrm{need} \\ $$$$\mathrm{find}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{of}\:\mathrm{P}=\mathrm{x}^{\mathrm{4}} +\mathrm{y}^{\mathrm{4}} \\ $$$$\mathrm{Since}\:\mathrm{x},\mathrm{y}>\mathrm{0},\mathrm{1}=\mathrm{x}+\mathrm{y}=\left(\sqrt{\mathrm{x}}−\sqrt{\mathrm{y}}\right)^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{xy}}\geqslant\mathrm{2}\sqrt{\mathrm{xy}} \\ $$$$\Rightarrow\sqrt{\mathrm{xy}}\leqslant\mathrm{1}/\mathrm{2}\Rightarrow\mathrm{xy}\leqslant\mathrm{1}/\mathrm{4}\left(\mathrm{1}\right).\mathrm{Hence}, \\ $$$$\mathrm{x}^{\mathrm{4}} +\mathrm{y}^{\mathrm{4}} =\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{4}} −\mathrm{4xy}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{4}} \right)−\mathrm{6x}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} \\ $$$$=\mathrm{1}−\mathrm{4xy}\left[\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} −\mathrm{2xy}\right]−\mathrm{6x}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} \\ $$$$=\mathrm{1}−\mathrm{4xy}\left(\mathrm{1}−\mathrm{2xy}\right)−\mathrm{6}\left(\mathrm{xy}\right)^{\mathrm{2}} =\mathrm{1}−\mathrm{4xy}+\mathrm{2}\left(\mathrm{xy}\right)^{\mathrm{2}} \\ $$$$=\mathrm{2}\left(\mathrm{xy}−\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} −\mathrm{3xy}+\frac{\mathrm{7}}{\mathrm{8}}\geqslant\mathrm{0}−\mathrm{3}.\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{7}}{\mathrm{8}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}.\mathrm{The}\:\mathrm{equality}\:\mathrm{ocurrs}\:\mathrm{if}\:\mathrm{and}\:\mathrm{only} \\ $$$$\mathrm{if}\:\mathrm{x}=\mathrm{y}=\mathrm{1}/\mathrm{2}\Leftrightarrow\mathrm{a}=\mathrm{b}=\:^{\mathrm{505}} \sqrt{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{Thus}\:\left(\mathrm{a}^{\mathrm{2020}} +\mathrm{b}^{\mathrm{2020}} \right)_{\mathrm{min}} =\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\mathrm{when}\:\mathrm{a}=\mathrm{b}=\frac{\mathrm{1}}{\:\:^{\mathrm{505}} \sqrt{\mathrm{2}}} \\ $$
Answered by bemath last updated on 23/Sep/20

