Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 115058 by mnjuly1970 last updated on 23/Sep/20

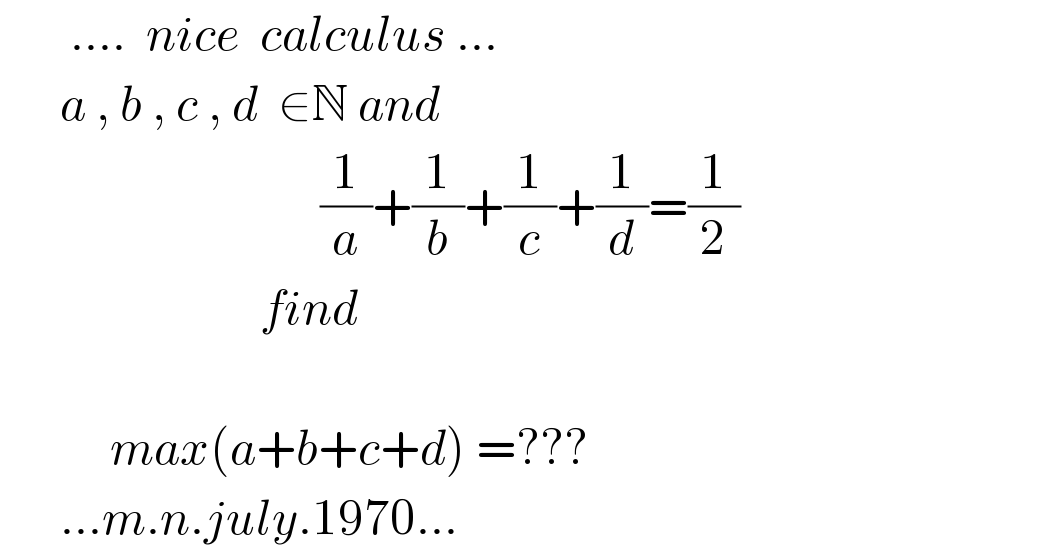
.... nice calculus ... a , b , c , d ∈N and (1/a)+(1/b)+(1/c)+(1/d)=(1/2) find max(a+b+c+d) =??? ...m.n.july.1970...

$$\:\:\:\:\:\:\:....\:\:{nice}\:\:{calculus}\:... \\ $$$$\:\:\:\:\:\:{a}\:,\:{b}\:,\:{c}\:,\:{d}\:\:\in\mathbb{N}\:{and}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}+\frac{\mathrm{1}}{{d}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{find}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{max}\left({a}+{b}+{c}+{d}\right)\:=??? \\ $$$$\:\:\:\:\:\:...{m}.{n}.{july}.\mathrm{1970}... \\ $$

Answered by 1549442205PVT last updated on 25/Sep/20

(1/a)+(1/b)+(1/c)+(1/d)=(1/2)(1) Since a,b,c,d are equal in role WLOG we can suppose that a≥b≥c≥d ⇒(4/a)≤ (1/a)+(1/b)+(1/c)+(1/d)=(1/2)≤(4/d) ⇒a≥8≥d≥3 i)Case d=3⇒ (1/a)+(1/b)+(1/c)=(1/2)−(1/3)=(1/6) ⇒(3/a)≤ (1/a)+(1/b)+(1/c)=(1/6)≤(3/c) ⇒a≥18≥c≥7 a)For c=7⇒ (1/a)+(1/b)=(1/6)−(1/7)=(1/(42)) ⇒(2/a)≤(1/a)+(1/b)=(1/(42))≤(2/b) ⇒a≥84≥b≥43 •if b=43 then (1/a)=(1/(42))−(1/(43))=(1/(1806)) ⇒a=1806 Thus,a+b+c+d=1806+43+7+3=1859 •If b=44⇒(1/a)=(1/(42))−(1/(44))=(1/(924))⇒a=924 42(a+b)=ab⇒(a−42)(b−42)=1764 =4.21^2 =2^2 .3^2 .7^2 b)For c=8⇒(1/a)+(1/b)=(1/6)−(1/8)=(1/(24)) ⇒ab=24(a+b)⇔(a−24)(b−24)=576 =24^2 =2^6 .3^2 b=25⇒a=600⇒a+b+c+d=636<1859 c)For c=9,10,...,18 by similar argument we see that a+b+c+d<1859 ii)d=4⇒(1/a)+(1/b)+(1/c)=(1/2)−(1/4)=(1/4) ⇒(3/a) ≤(1/4)≤(3/c)⇒a≥12≥c≥5 a)For c=5⇒(1/a)+(1/b)=(1/4)−(1/5)=(1/(20)) ⇒ab=20(a+b)⇔(a−20)(b−20)=400=2^4 .5^2 •if b=21⇒a=420⇒a+b+c+d=450<1859 b)For c=6...12^(−) ,by similar argument we get a+b+c+d<1859 ii)Cases d=5...8^(−) ,repeating above argument we obtain a+b+c+d<1859 Thus,if (1/a)+(1/b)+(1/c)+(1/d)=(1/2) with a,b,c,d∈N then max(a+b+c+d)=1859

$$\:\:\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}+\frac{\mathrm{1}}{{d}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}\right) \\ $$$$\mathrm{Since}\:\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}\:\mathrm{are}\:\mathrm{equal}\:\mathrm{in}\:\mathrm{role}\:\mathrm{WLOG} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{suppose}\:\mathrm{that}\:\mathrm{a}\geqslant\mathrm{b}\geqslant\mathrm{c}\geqslant\mathrm{d} \\ $$$$\Rightarrow\frac{\mathrm{4}}{\mathrm{a}}\leqslant\:\:\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}+\frac{\mathrm{1}}{{d}}=\frac{\mathrm{1}}{\mathrm{2}}\leqslant\frac{\mathrm{4}}{\mathrm{d}} \\ $$$$\Rightarrow\mathrm{a}\geqslant\mathrm{8}\geqslant\mathrm{d}\geqslant\mathrm{3} \\ $$$$\left.\mathrm{i}\right)\mathrm{Case}\:\mathrm{d}=\mathrm{3}\Rightarrow\:\:\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\Rightarrow\frac{\mathrm{3}}{\mathrm{a}}\leqslant\:\:\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}=\frac{\mathrm{1}}{\mathrm{6}}\leqslant\frac{\mathrm{3}}{\mathrm{c}} \\ $$$$\Rightarrow\mathrm{a}\geqslant\mathrm{18}\geqslant\mathrm{c}\geqslant\mathrm{7} \\ $$$$\left.\mathrm{a}\right)\mathrm{For}\:\mathrm{c}=\mathrm{7}\Rightarrow\:\:\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}=\frac{\mathrm{1}}{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{7}}=\frac{\mathrm{1}}{\mathrm{42}} \\ $$$$\Rightarrow\frac{\mathrm{2}}{\mathrm{a}}\leqslant\frac{\mathrm{1}}{\mathrm{a}}+\frac{\mathrm{1}}{\mathrm{b}}=\frac{\mathrm{1}}{\mathrm{42}}\leqslant\frac{\mathrm{2}}{\mathrm{b}} \\ $$$$\Rightarrow\mathrm{a}\geqslant\mathrm{84}\geqslant\mathrm{b}\geqslant\mathrm{43} \\ $$$$\bullet\mathrm{if}\:\mathrm{b}=\mathrm{43}\:\mathrm{then}\:\frac{\mathrm{1}}{\mathrm{a}}=\frac{\mathrm{1}}{\mathrm{42}}−\frac{\mathrm{1}}{\mathrm{43}}=\frac{\mathrm{1}}{\mathrm{1806}} \\ $$$$\Rightarrow\mathrm{a}=\mathrm{1806} \\ $$$$\mathrm{Thus},\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}=\mathrm{1806}+\mathrm{43}+\mathrm{7}+\mathrm{3}=\mathrm{1859} \\ $$$$\bullet\mathrm{If}\:\mathrm{b}=\mathrm{44}\Rightarrow\frac{\mathrm{1}}{\mathrm{a}}=\frac{\mathrm{1}}{\mathrm{42}}−\frac{\mathrm{1}}{\mathrm{44}}=\frac{\mathrm{1}}{\mathrm{924}}\Rightarrow\mathrm{a}=\mathrm{924} \\ $$$$\mathrm{42}\left(\mathrm{a}+\mathrm{b}\right)=\mathrm{ab}\Rightarrow\left(\mathrm{a}−\mathrm{42}\right)\left(\mathrm{b}−\mathrm{42}\right)=\mathrm{1764} \\ $$$$=\mathrm{4}.\mathrm{21}^{\mathrm{2}} =\mathrm{2}^{\mathrm{2}} .\mathrm{3}^{\mathrm{2}} .\mathrm{7}^{\mathrm{2}} \\ $$$$\left.\mathrm{b}\right)\mathrm{For}\:\mathrm{c}=\mathrm{8}\Rightarrow\frac{\mathrm{1}}{\mathrm{a}}+\frac{\mathrm{1}}{\mathrm{b}}=\frac{\mathrm{1}}{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{8}}=\frac{\mathrm{1}}{\mathrm{24}} \\ $$$$\Rightarrow\mathrm{ab}=\mathrm{24}\left(\mathrm{a}+\mathrm{b}\right)\Leftrightarrow\left(\mathrm{a}−\mathrm{24}\right)\left(\mathrm{b}−\mathrm{24}\right)=\mathrm{576} \\ $$$$=\mathrm{24}^{\mathrm{2}} =\mathrm{2}^{\mathrm{6}} .\mathrm{3}^{\mathrm{2}} \\ $$$$\mathrm{b}=\mathrm{25}\Rightarrow\mathrm{a}=\mathrm{600}\Rightarrow\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}=\mathrm{636}<\mathrm{1859} \\ $$$$\left.\mathrm{c}\right)\mathrm{For}\:\mathrm{c}=\mathrm{9},\mathrm{10},...,\mathrm{18}\:\mathrm{by}\:\:\mathrm{similar}\:\mathrm{argument} \\ $$$$\mathrm{we}\:\mathrm{see}\:\mathrm{that}\:\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}<\mathrm{1859} \\ $$$$\left.\mathrm{ii}\right)\mathrm{d}=\mathrm{4}\Rightarrow\frac{\mathrm{1}}{\mathrm{a}}+\frac{\mathrm{1}}{\mathrm{b}}+\frac{\mathrm{1}}{\mathrm{c}}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\frac{\mathrm{3}}{\mathrm{a}}\:\leqslant\frac{\mathrm{1}}{\mathrm{4}}\leqslant\frac{\mathrm{3}}{\mathrm{c}}\Rightarrow\mathrm{a}\geqslant\mathrm{12}\geqslant\mathrm{c}\geqslant\mathrm{5} \\ $$$$\left.\mathrm{a}\right)\mathrm{For}\:\mathrm{c}=\mathrm{5}\Rightarrow\frac{\mathrm{1}}{\mathrm{a}}+\frac{\mathrm{1}}{\mathrm{b}}=\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{5}}=\frac{\mathrm{1}}{\mathrm{20}} \\ $$$$\Rightarrow\mathrm{ab}=\mathrm{20}\left(\mathrm{a}+\mathrm{b}\right)\Leftrightarrow\left(\mathrm{a}−\mathrm{20}\right)\left(\mathrm{b}−\mathrm{20}\right)=\mathrm{400}=\mathrm{2}^{\mathrm{4}} .\mathrm{5}^{\mathrm{2}} \\ $$$$\bullet\mathrm{if}\:\mathrm{b}=\mathrm{21}\Rightarrow\mathrm{a}=\mathrm{420}\Rightarrow\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}=\mathrm{450}<\mathrm{1859} \\ $$$$\left.\mathrm{b}\right)\mathrm{For}\:\mathrm{c}=\overline {\mathrm{6}...\mathrm{12}},\mathrm{by}\:\mathrm{similar}\:\mathrm{argument} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}<\mathrm{1859} \\ $$$$\left.\mathrm{ii}\right)\mathrm{Cases}\:\mathrm{d}=\overline {\mathrm{5}...\mathrm{8}},\mathrm{repeating}\:\mathrm{above}\:\mathrm{argument}\: \\ $$$$\mathrm{we}\:\mathrm{obtain}\:\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}<\mathrm{1859} \\ $$$$\mathrm{Thus},\mathrm{if}\:\:\:\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}+\frac{\mathrm{1}}{{d}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{with}\:\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}\in\mathrm{N}\:\mathrm{then} \\ $$$$\mathrm{max}\left(\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d}\right)=\mathrm{1859} \\ $$

Commented by mnjuly1970 last updated on 23/Sep/20

verh excellent. thank you..

$${verh}\:{excellent}.\:{thank}\:{you}.. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com