Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 115122 by bobhans last updated on 23/Sep/20

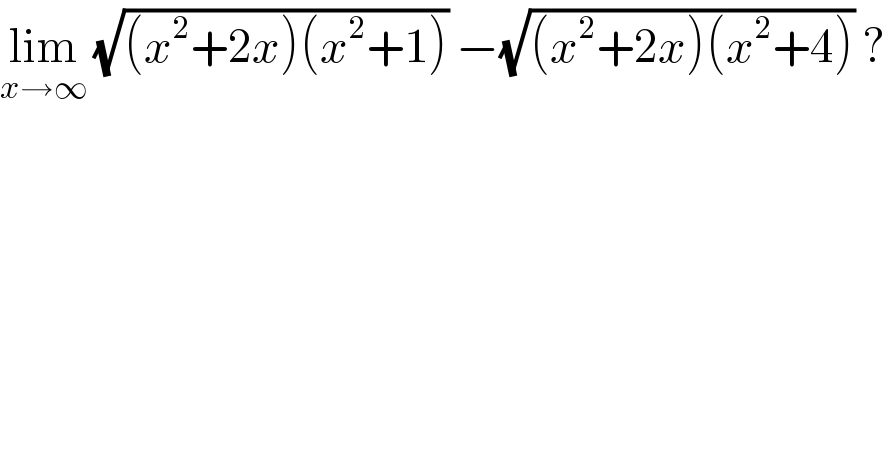
lim_(x→∞) (√((x^2 +2x)(x^2 +1))) −(√((x^2 +2x)(x^2 +4))) ?

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\left({x}^{\mathrm{2}} +\mathrm{2}{x}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)}\:−\sqrt{\left({x}^{\mathrm{2}} +\mathrm{2}{x}\right)\left({x}^{\mathrm{2}} +\mathrm{4}\right)}\:? \\ $$

Commented by malwan last updated on 23/Sep/20

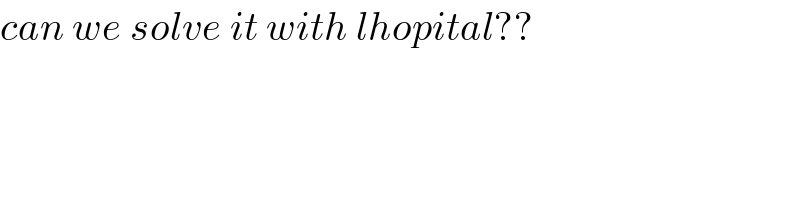
can we solve it with lhopital??

$${can}\:{we}\:{solve}\:{it}\:{with}\:{lhopital}?? \\ $$

Answered by john santu last updated on 23/Sep/20

lim_(x→∞) (√(x^2 +2x)) ((√(x^2 +1))−(√(x^2 +4)))= lim_(x→∞) (√(x^2 +2x)) (((−3)/( (√(x^2 +1))+(√(x^2 +4))))) = −3 ×lim_(x→∞) ((x (√(1+(2/x))))/(x ((√(1+(1/x)))+(√(1+(4/x)))))) = −(3/2).

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}}\:\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}−\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}\right)= \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}}\:\left(\frac{−\mathrm{3}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}+\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}}\right)\:= \\ $$$$−\mathrm{3}\:×\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{x}\:\sqrt{\mathrm{1}+\frac{\mathrm{2}}{{x}}}}{{x}\:\left(\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}}}+\sqrt{\mathrm{1}+\frac{\mathrm{4}}{{x}}}\right)}\:= \\ $$$$−\frac{\mathrm{3}}{\mathrm{2}}. \\ $$

Answered by bemath last updated on 23/Sep/20

Answered by Dwaipayan Shikari last updated on 23/Sep/20

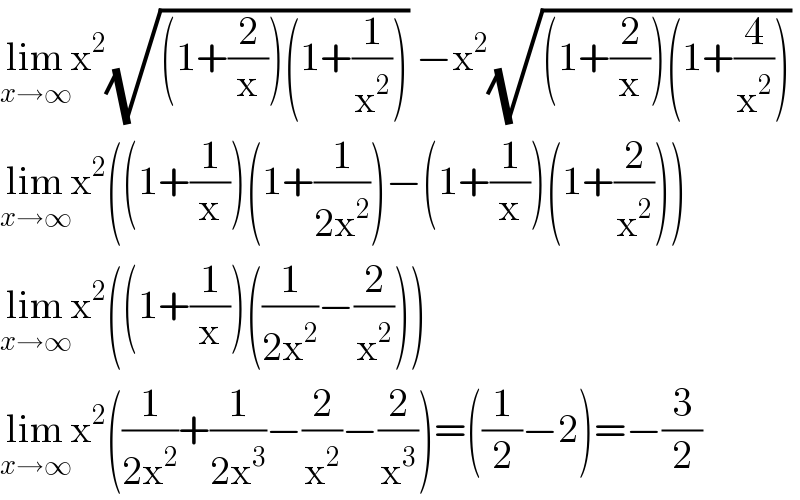
lim_(x→∞) x^2 (√((1+(2/x))(1+(1/x^2 )))) −x^2 (√((1+(2/x))(1+(4/x^2 )))) lim_(x→∞) x^2 ((1+(1/x))(1+(1/(2x^2 )))−(1+(1/x))(1+(2/x^2 ))) lim_(x→∞) x^2 ((1+(1/x))((1/(2x^2 ))−(2/x^2 ))) lim_(x→∞) x^2 ((1/(2x^2 ))+(1/(2x^3 ))−(2/x^2 )−(2/x^3 ))=((1/2)−2)=−(3/2)

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}x}^{\mathrm{2}} \sqrt{\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{x}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)}\:−\mathrm{x}^{\mathrm{2}} \sqrt{\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{x}}\right)\left(\mathrm{1}+\frac{\mathrm{4}}{\mathrm{x}^{\mathrm{2}} }\right)} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}x}^{\mathrm{2}} \left(\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2x}^{\mathrm{2}} }\right)−\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}\right)\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{2}} }\right)\right) \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}x}^{\mathrm{2}} \left(\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}\right)\left(\frac{\mathrm{1}}{\mathrm{2x}^{\mathrm{2}} }−\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{2}} }\right)\right) \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}x}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2x}^{\mathrm{3}} }−\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{3}} }\right)=\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}\right)=−\frac{\mathrm{3}}{\mathrm{2}} \\ $$

Answered by Bird last updated on 24/Sep/20

let f(x) =(√((x^2 +2x)(x^2 +1)))−(√((x^2 +2x)(x^2 +4))) f(x)=x^2 (√((1+(2/x)))).(√(1+(1/x^2 )))−x^2 (√(1+(2/x))).(√(1+(4/x^2 ))) f(x)∼x^2 (1+(1/x))(1+(1/(2x^2 ))) −x^2 (1+(1/x))(1+(2/x^2 ))(x→∞) ⇒ f(x)∼(1+(1/x)){x^2 +(1/2)−x^2 −2} f(x)∼(1+(1/x))(−(3/2)) ⇒ lim_(x→∞) f(x) =−(3/2)

$${let}\:{f}\left({x}\right)\:=\sqrt{\left({x}^{\mathrm{2}} +\mathrm{2}{x}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)}−\sqrt{\left({x}^{\mathrm{2}} +\mathrm{2}{x}\right)\left({x}^{\mathrm{2}} +\mathrm{4}\right)} \\ $$$${f}\left({x}\right)={x}^{\mathrm{2}} \sqrt{\left(\mathrm{1}+\frac{\mathrm{2}}{{x}}\right)}.\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}−{x}^{\mathrm{2}} \sqrt{\mathrm{1}+\frac{\mathrm{2}}{{x}}}.\sqrt{\mathrm{1}+\frac{\mathrm{4}}{{x}^{\mathrm{2}} }} \\ $$$${f}\left({x}\right)\sim{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\right) \\ $$$$−{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)\left(\mathrm{1}+\frac{\mathrm{2}}{{x}^{\mathrm{2}} }\right)\left({x}\rightarrow\infty\right)\:\Rightarrow \\ $$$${f}\left({x}\right)\sim\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)\left\{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}−{x}^{\mathrm{2}} −\mathrm{2}\right\} \\ $$$${f}\left({x}\right)\sim\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\infty} {f}\left({x}\right)\:=−\frac{\mathrm{3}}{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com