Question Number 115133 by ZiYangLee last updated on 23/Sep/20

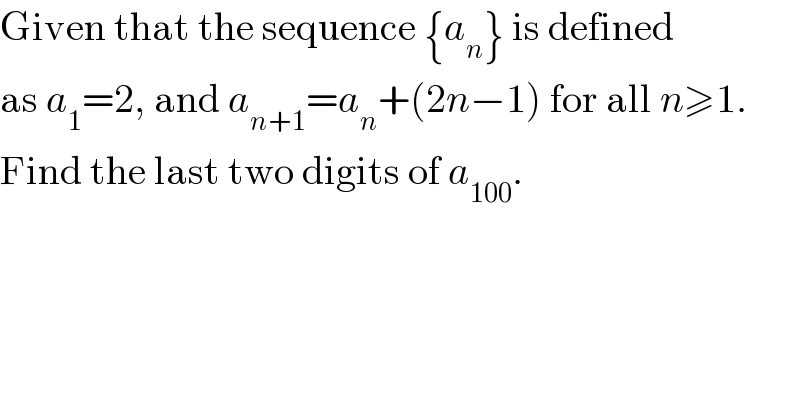
Given that the sequence {a_n } is defined as a_1 =2, and a_(n+1) =a_n +(2n−1) for all n≥1. Find the last two digits of a_(100) .

Answered by Olaf last updated on 23/Sep/20

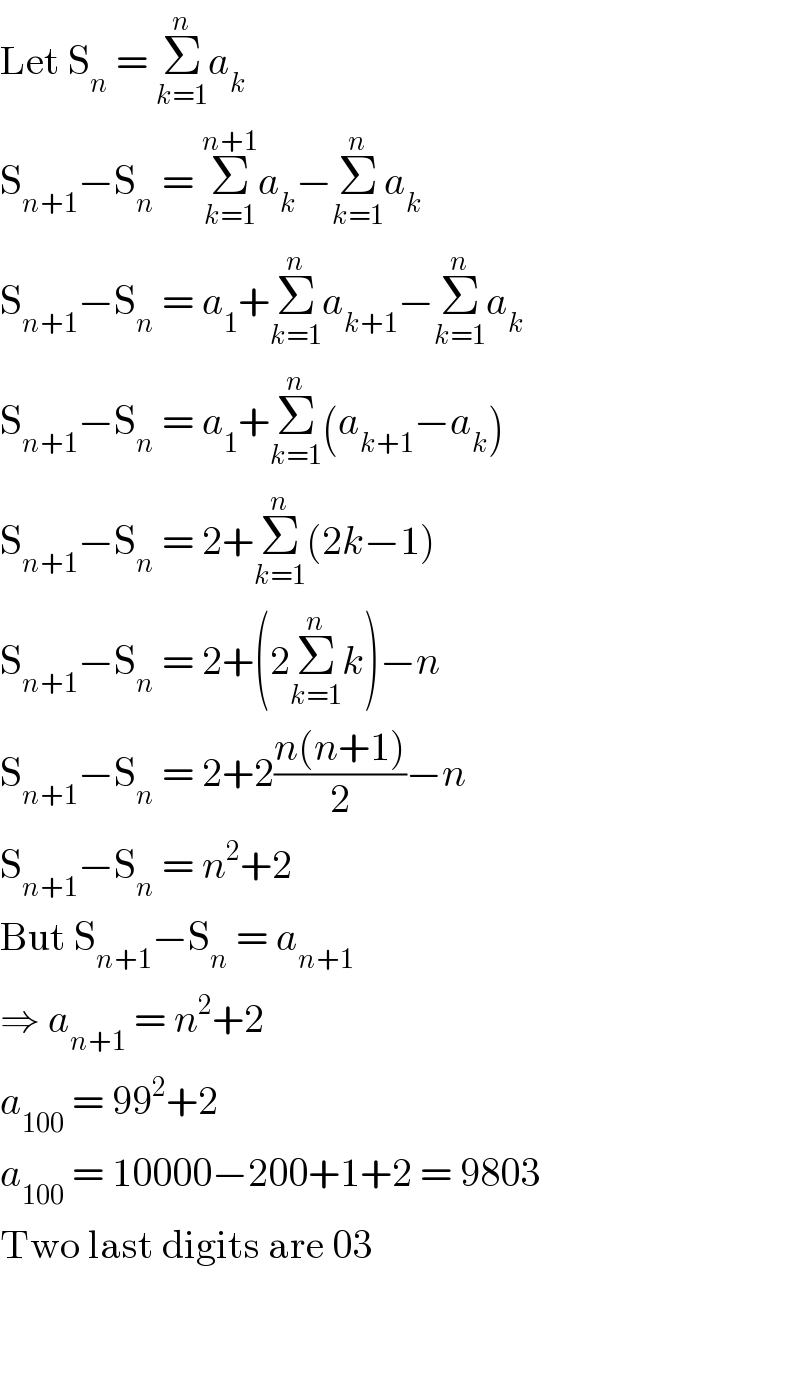
Let S_n = Σ_(k=1) ^n a_k S_(n+1) −S_n = Σ_(k=1) ^(n+1) a_k −Σ_(k=1) ^n a_k S_(n+1) −S_n = a_1 +Σ_(k=1) ^n a_(k+1) −Σ_(k=1) ^n a_k S_(n+1) −S_n = a_1 +Σ_(k=1) ^n (a_(k+1) −a_k ) S_(n+1) −S_n = 2+Σ_(k=1) ^n (2k−1) S_(n+1) −S_n = 2+(2Σ_(k=1) ^n k)−n S_(n+1) −S_n = 2+2((n(n+1))/2)−n S_(n+1) −S_n = n^2 +2 But S_(n+1) −S_n = a_(n+1) ⇒ a_(n+1) = n^2 +2 a_(100) = 99^2 +2 a_(100) = 10000−200+1+2 = 9803 Two last digits are 03

Answered by Dwaipayan Shikari last updated on 23/Sep/20

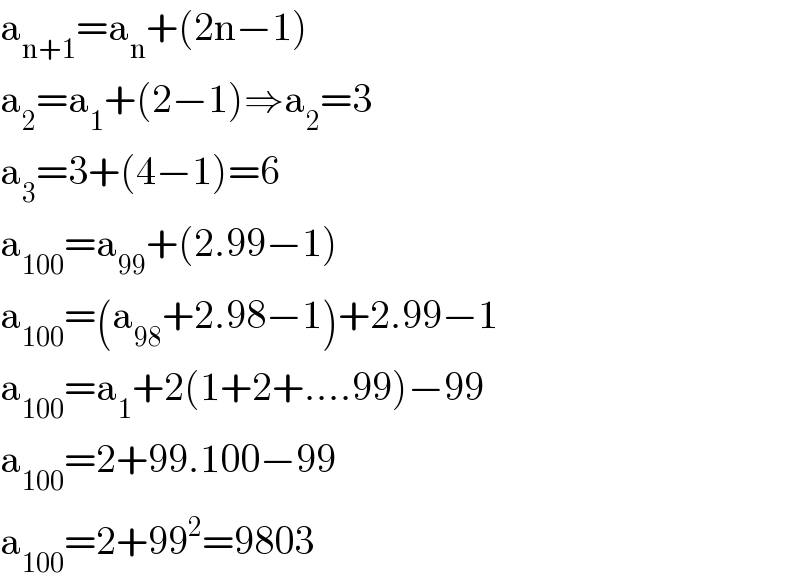
a_(n+1) =a_n +(2n−1) a_2 =a_1 +(2−1)⇒a_2 =3 a_3 =3+(4−1)=6 a_(100) =a_(99) +(2.99−1) a_(100) =(a_(98) +2.98−1)+2.99−1 a_(100) =a_1 +2(1+2+....99)−99 a_(100) =2+99.100−99 a_(100) =2+99^2 =9803

Answered by Bird last updated on 24/Sep/20

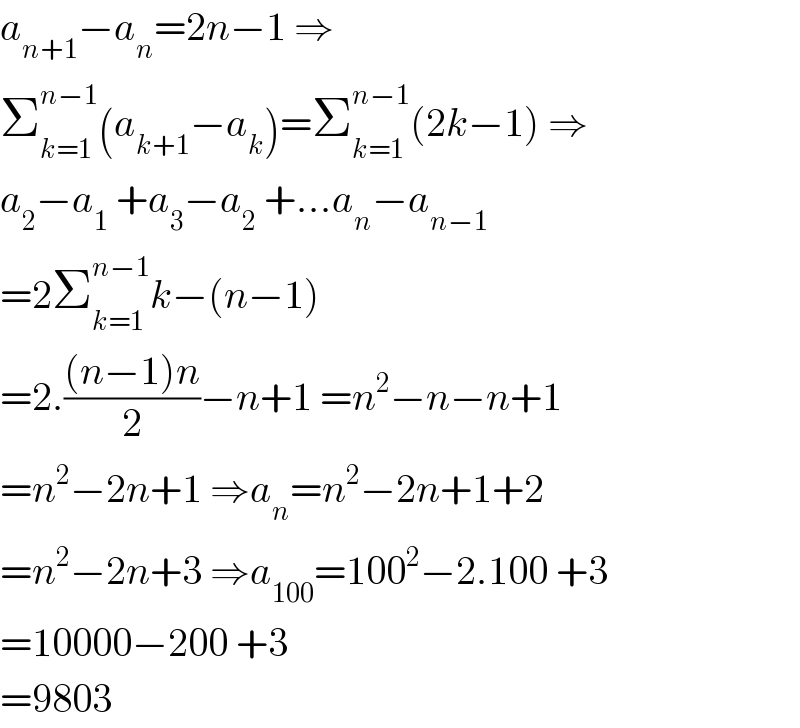
a_(n+1) −a_n =2n−1 ⇒ Σ_(k=1) ^(n−1) (a_(k+1) −a_k )=Σ_(k=1) ^(n−1) (2k−1) ⇒ a_2 −a_1 +a_3 −a_2 +...a_n −a_(n−1) =2Σ_(k=1) ^(n−1) k−(n−1) =2.(((n−1)n)/2)−n+1 =n^2 −n−n+1 =n^2 −2n+1 ⇒a_n =n^2 −2n+1+2 =n^2 −2n+3 ⇒a_(100) =100^2 −2.100 +3 =10000−200 +3 =9803