Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 115166 by I want to learn more last updated on 24/Sep/20

Answered by 1549442205PVT last updated on 24/Sep/20

$$77°$$

Commented by I want to learn more last updated on 24/Sep/20

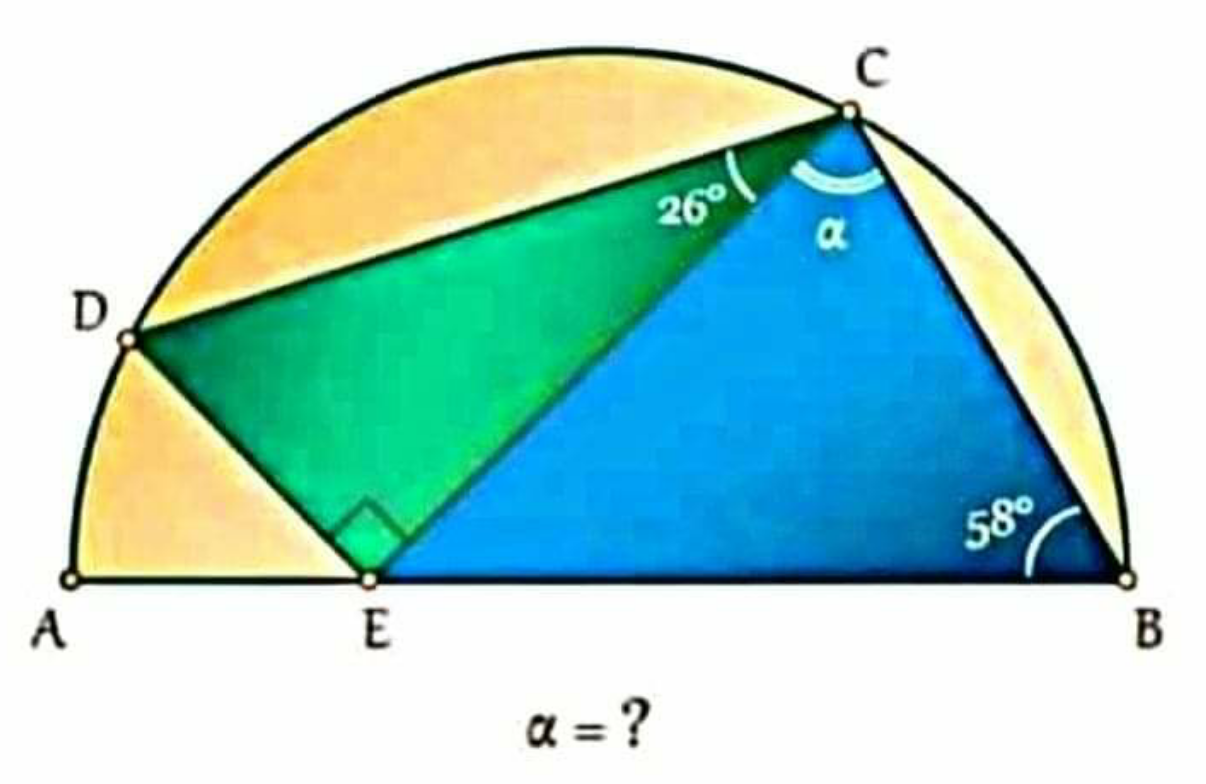
$$\mathrm{please}\mathrm{workings}\mathrm{sir}$$

Answered by 1549442205PVT last updated on 24/Sep/20

Commented by 1549442205PVT last updated on 24/Sep/20

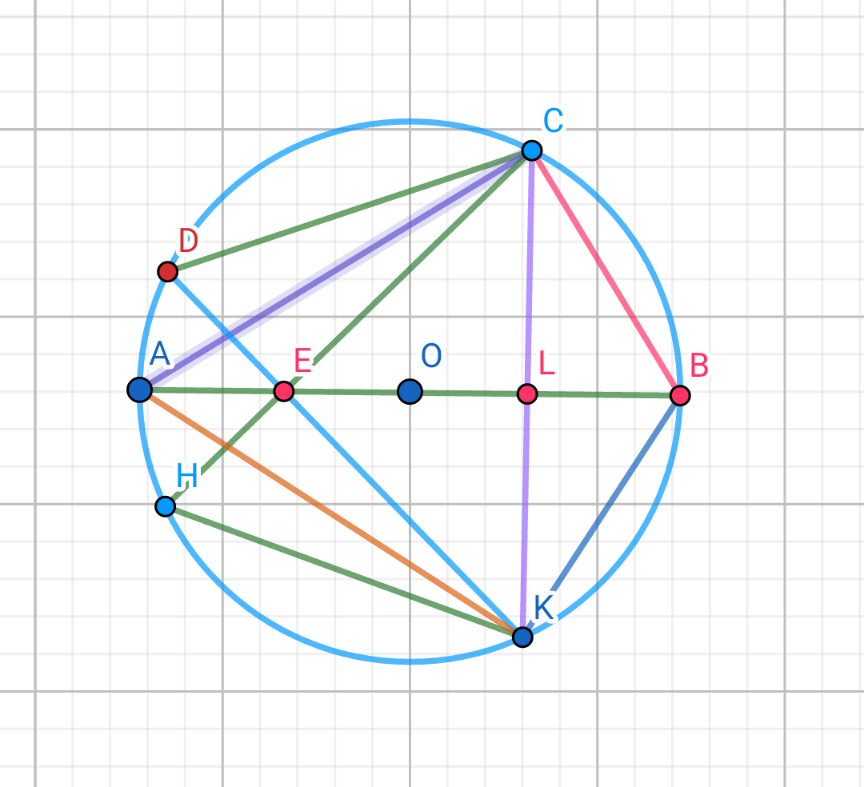
$$\mathrm{Draw}\mathrm{the}\mathrm{circum}\mathrm{circle}\left(\mathrm{O}\right)\mathrm{of}\mathrm{\Delta }\mathrm{ABC}$$$$\mathrm{and}\mathrm{denote}\mathrm{K}=\left(\mathrm{O}\right)\cap \left(\mathrm{DE}\right),\mathrm{L}=\mathrm{AB}\cap \mathrm{CK}$$$$\mathrm{H}=\left(\mathrm{O}\right)\cap \left(\mathrm{CE}\right)$$$$\mathrm{From}\mathrm{the}\mathrm{hypothesis}\mathrm{\Delta }\mathrm{CDE}\mathrm{is}\mathrm{right}$$$$\mathrm{at}\mathrm{E}\mathrm{and}\widehat{\mathrm{DCE}}=26°\Rightarrow \widehat{\mathrm{CDK}}=64°,$$$$\mathrm{\Delta }\mathrm{ACB}\mathrm{is}\mathrm{right}\mathrm{at}\mathrm{C}\mathrm{and}\widehat{\mathrm{ABC}}=58°$$$$\Rightarrow \widehat{\mathrm{BAC}}=32°=\frac{1}{2}\widehat{\mathrm{CDK}}\Rightarrow \stackrel{⌢}{\mathrm{CBK}}=2\stackrel{⌢}{\mathrm{BC}}$$$$\Rightarrow \stackrel{⌢}{\mathrm{BC}}=\stackrel{⌢}{\mathrm{BK}}\Rightarrow \mathrm{AB}\mathrm{\perp }\mathrm{CK}\mathrm{at}\mathrm{L}(\mathrm{the}\mathrm{property}$$$$\mathrm{of}\mathrm{the}\mathrm{diameter}\mathrm{of}\mathrm{a}\mathrm{circle})\mathrm{and}\mathrm{BC}=\mathrm{BK},\mathrm{LC}=\mathrm{LK}$$$$\mathrm{It}\mathrm{follows}\mathrm{that}\mathrm{the}\mathrm{triangles}\mathrm{BCK}\mathrm{and}$$$$\mathrm{ECK}\mathrm{are}\mathrm{isosceles}\mathrm{at}\mathrm{B}\mathrm{and}\mathrm{E}.\mathrm{Hence},$$$$\widehat{\mathrm{AED}}=\widehat{\mathrm{AEH}}=\widehat{\mathrm{BEC}}=\widehat{\mathrm{BEK}}=\phi$$$$\Rightarrow \stackrel{⌢}{\mathrm{AD}}=\stackrel{⌢}{\mathrm{AH}}\Rightarrow \mathrm{CA}\mathrm{is}\mathrm{the}\mathrm{bisector}\mathrm{of}$$$$\mathrm{the}\mathrm{angle}\widehat{\mathrm{DCE}}=26°\Rightarrow \widehat{\mathrm{ACD}}=\widehat{\mathrm{ACH}}=13°$$$$\Rightarrow \alpha =\widehat{\mathrm{ACB}}-\widehat{\mathrm{ACH}}=90°-13°=77°$$$$\mathrm{Answer}\alpha =77°$$

Commented by I want to learn more last updated on 24/Sep/20

$$\mathrm{Thanks}\mathrm{sir}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com