Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 11517 by Joel576 last updated on 27/Mar/17

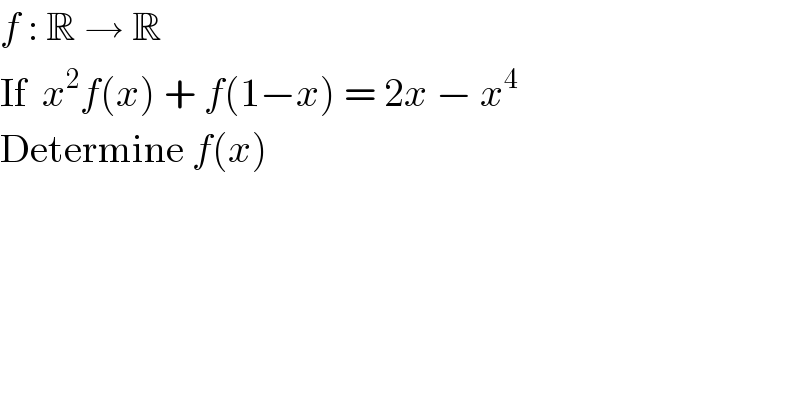
f : R → R If x^2 f(x) + f(1−x) = 2x − x^4 Determine f(x)

$${f}\::\:\mathbb{R}\:\rightarrow\:\mathbb{R} \\ $$$$\mathrm{If}\:\:{x}^{\mathrm{2}} {f}\left({x}\right)\:+\:{f}\left(\mathrm{1}−{x}\right)\:=\:\mathrm{2}{x}\:−\:{x}^{\mathrm{4}} \\ $$$$\mathrm{Determine}\:{f}\left({x}\right) \\ $$

Answered by sma3l2996 last updated on 27/Mar/17

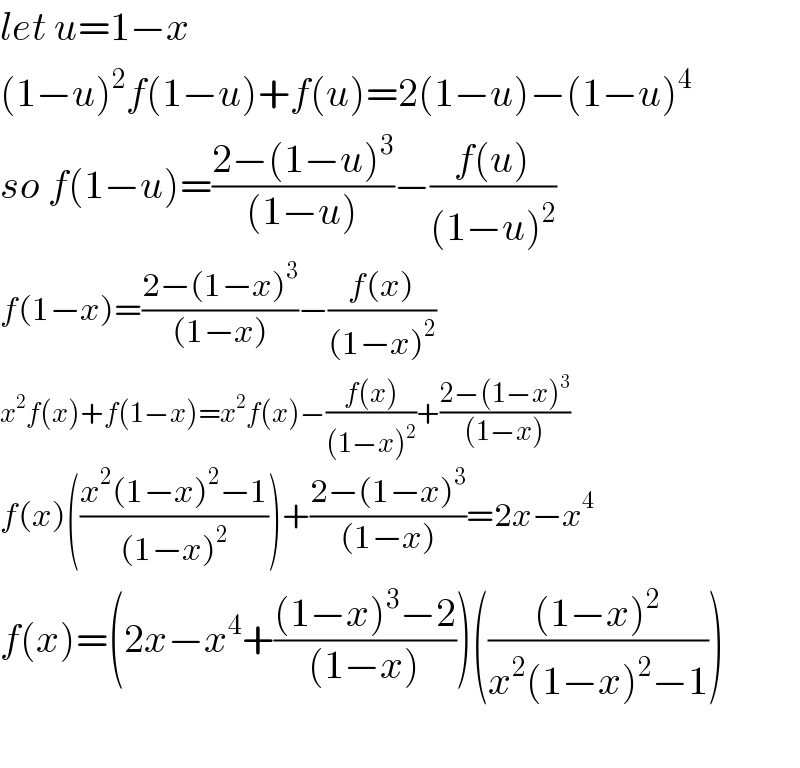
let u=1−x (1−u)^2 f(1−u)+f(u)=2(1−u)−(1−u)^4 so f(1−u)=((2−(1−u)^3 )/((1−u)))−((f(u))/((1−u)^2 )) f(1−x)=((2−(1−x)^3 )/((1−x)))−((f(x))/((1−x)^2 )) x^2 f(x)+f(1−x)=x^2 f(x)−((f(x))/((1−x)^2 ))+((2−(1−x)^3 )/((1−x))) f(x)(((x^2 (1−x)^2 −1)/((1−x)^2 )))+((2−(1−x)^3 )/((1−x)))=2x−x^4 f(x)=(2x−x^4 +(((1−x)^3 −2)/((1−x))))((((1−x)^2 )/(x^2 (1−x)^2 −1)))

$${let}\:{u}=\mathrm{1}−{x} \\ $$$$\left(\mathrm{1}−{u}\right)^{\mathrm{2}} {f}\left(\mathrm{1}−{u}\right)+{f}\left({u}\right)=\mathrm{2}\left(\mathrm{1}−{u}\right)−\left(\mathrm{1}−{u}\right)^{\mathrm{4}} \\ $$$${so}\:{f}\left(\mathrm{1}−{u}\right)=\frac{\mathrm{2}−\left(\mathrm{1}−{u}\right)^{\mathrm{3}} }{\left(\mathrm{1}−{u}\right)}−\frac{{f}\left({u}\right)}{\left(\mathrm{1}−{u}\right)^{\mathrm{2}} } \\ $$$${f}\left(\mathrm{1}−{x}\right)=\frac{\mathrm{2}−\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }{\left(\mathrm{1}−{x}\right)}−\frac{{f}\left({x}\right)}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} } \\ $$$${x}^{\mathrm{2}} {f}\left({x}\right)+{f}\left(\mathrm{1}−{x}\right)={x}^{\mathrm{2}} {f}\left({x}\right)−\frac{{f}\left({x}\right)}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{\mathrm{2}−\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }{\left(\mathrm{1}−{x}\right)} \\ $$$${f}\left({x}\right)\left(\frac{{x}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\right)+\frac{\mathrm{2}−\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }{\left(\mathrm{1}−{x}\right)}=\mathrm{2}{x}−{x}^{\mathrm{4}} \\ $$$${f}\left({x}\right)=\left(\mathrm{2}{x}−{x}^{\mathrm{4}} +\frac{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} −\mathrm{2}}{\left(\mathrm{1}−{x}\right)}\right)\left(\frac{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)^{\mathrm{2}} −\mathrm{1}}\right) \\ $$$$ \\ $$

Commented by Joel576 last updated on 28/Mar/17

thank you very much

$${thank}\:{you}\:{very}\:{much} \\ $$

Commented by Joel576 last updated on 28/Mar/17

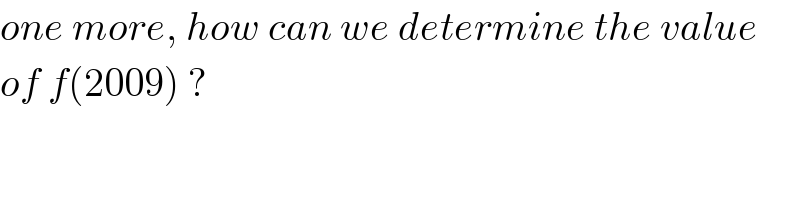
one more, how can we determine the value of f(2009) ?

$${one}\:{more},\:{how}\:{can}\:{we}\:{determine}\:{the}\:{value} \\ $$$${of}\:{f}\left(\mathrm{2009}\right)\:? \\ $$

Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 28/Mar/17

x^2 f(x)+f(1−x)=2x−x^4 (1−x)^2 f(1−x)+f(x)=2(1−x)−(1−x)^4 [x^2 (1−x)^2 −1]f(x)=(2x−x^4 )(1−x)^2 −2(1−x)+(1−x)^4 = (1−x)[2x−x^4 −2x^2 +x^5 −2+1−3x+3x^2 −x^3 )= (1−x)(x^5 −x^4 −x^3 +x^2 −x−1)= −x^6 +x^5 +x^4 −x^3 +x^2 +x+x^5 −x^4 −x^3 +x^2 −x−1= −(x^6 −2x^5 +2x^3 −2x^2 +1)= −(x^3 −x^2 +1)^2 +x^4 =(x^2 +x^3 −x^2 +1)(x^2 −x^3 +x^2 −1)= (x^3 +1)(−x^3 +2x^2 −1)=(x^3 +1)(−x(x^2 −2x+1)−(1−x))= (x^3 +1)(−x(1−x)^2 −(1−x)) ⇒f(x)=(((1+x)(1−x+x^2 )(1−x)(1+x(1−x)))/((1−x(1−x))(1+x(1−x))))= f(x)=(1−x)(1+x)=1−x^2 f(2009)=(1−2009)(1+2009)= −2010×2008

$${x}^{\mathrm{2}} {f}\left({x}\right)+{f}\left(\mathrm{1}−{x}\right)=\mathrm{2}{x}−{x}^{\mathrm{4}} \\ $$$$\left(\mathrm{1}−{x}\right)^{\mathrm{2}} {f}\left(\mathrm{1}−{x}\right)+{f}\left({x}\right)=\mathrm{2}\left(\mathrm{1}−{x}\right)−\left(\mathrm{1}−{x}\right)^{\mathrm{4}} \\ $$$$\left[{x}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)^{\mathrm{2}} −\mathrm{1}\right]{f}\left({x}\right)=\left(\mathrm{2}{x}−{x}^{\mathrm{4}} \right)\left(\mathrm{1}−{x}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{1}−{x}\right)+\left(\mathrm{1}−{x}\right)^{\mathrm{4}} = \\ $$$$\left(\mathrm{1}−{x}\right)\left[\mathrm{2}{x}−{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} +{x}^{\mathrm{5}} −\mathrm{2}+\mathrm{1}−\mathrm{3}{x}+\mathrm{3}{x}^{\mathrm{2}} −{x}^{\mathrm{3}} \right)= \\ $$$$\left(\mathrm{1}−{x}\right)\left({x}^{\mathrm{5}} −{x}^{\mathrm{4}} −{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −{x}−\mathrm{1}\right)= \\ $$$$−{x}^{\mathrm{6}} +{x}^{\mathrm{5}} +{x}^{\mathrm{4}} −{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+{x}^{\mathrm{5}} −{x}^{\mathrm{4}} −{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −{x}−\mathrm{1}= \\ $$$$−\left({x}^{\mathrm{6}} −\mathrm{2}{x}^{\mathrm{5}} +\mathrm{2}{x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right)= \\ $$$$−\left({x}^{\mathrm{3}} −{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} +{x}^{\mathrm{4}} =\left({x}^{\mathrm{2}} +{x}^{\mathrm{3}} −{x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −\mathrm{1}\right)= \\ $$$$\left({x}^{\mathrm{3}} +\mathrm{1}\right)\left(−{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}\right)=\left({x}^{\mathrm{3}} +\mathrm{1}\right)\left(−{x}\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\right)−\left(\mathrm{1}−{x}\right)\right)= \\ $$$$\left({x}^{\mathrm{3}} +\mathrm{1}\right)\left(−{x}\left(\mathrm{1}−{x}\right)^{\mathrm{2}} −\left(\mathrm{1}−{x}\right)\right) \\ $$$$\Rightarrow{f}\left({x}\right)=\frac{\left(\mathrm{1}+{x}\right)\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}−{x}\right)\left(\mathrm{1}+{x}\left(\mathrm{1}−{x}\right)\right)}{\left(\mathrm{1}−{x}\left(\mathrm{1}−{x}\right)\right)\left(\mathrm{1}+{x}\left(\mathrm{1}−{x}\right)\right)}= \\ $$$${f}\left({x}\right)=\left(\mathrm{1}−{x}\right)\left(\mathrm{1}+{x}\right)=\mathrm{1}−{x}^{\mathrm{2}} \\ $$$${f}\left(\mathrm{2009}\right)=\left(\mathrm{1}−\mathrm{2009}\right)\left(\mathrm{1}+\mathrm{2009}\right)= \\ $$$$−\mathrm{2010}×\mathrm{2008} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com