Question Number 115170 by bobhans last updated on 24/Sep/20

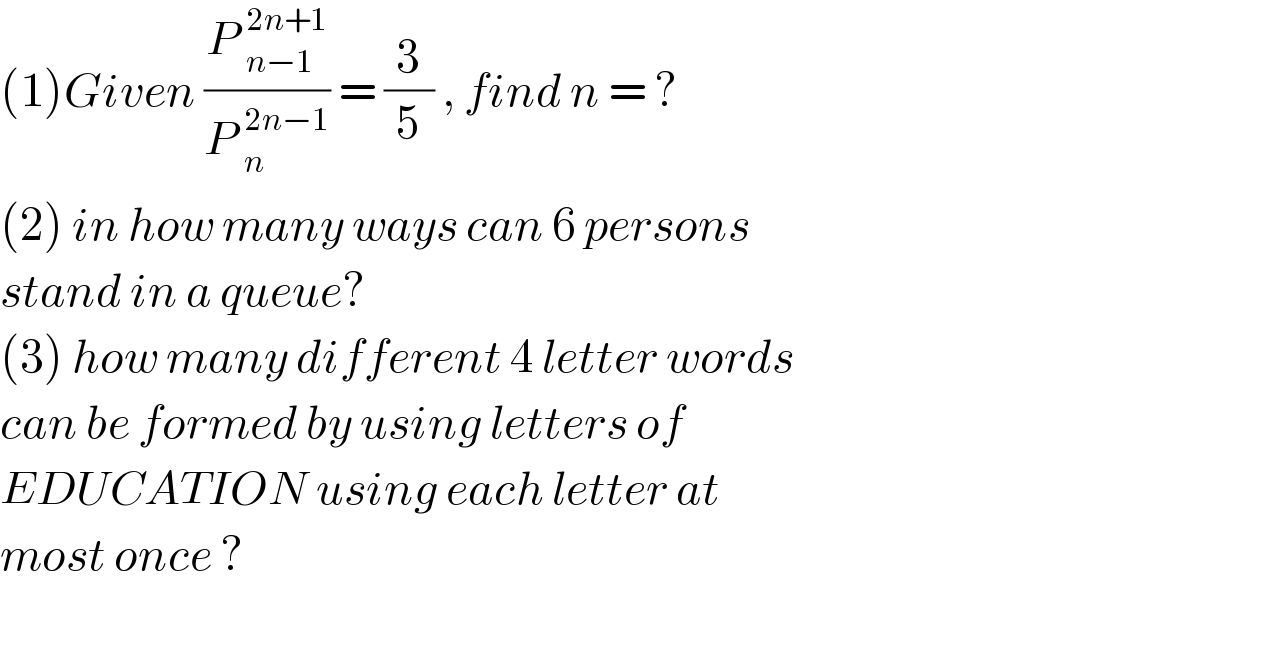
(1)Given ((P _(n−1)^(2n+1) )/(P _n^(2n−1) )) = (3/5) , find n = ? (2) in how many ways can 6 persons stand in a queue? (3) how many different 4 letter words can be formed by using letters of EDUCATION using each letter at most once ?

Answered by bemath last updated on 24/Sep/20

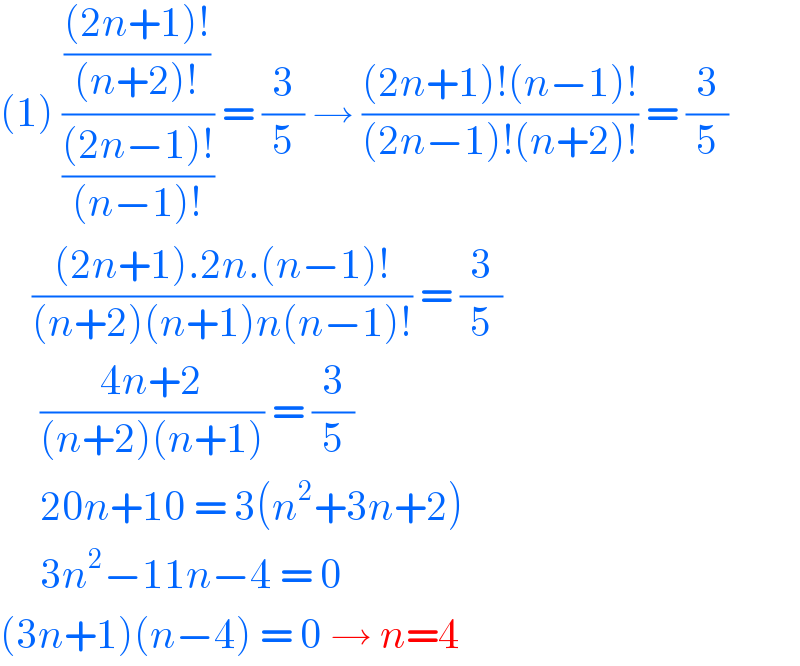
(1) ((((2n+1)!)/((n+2)!))/(((2n−1)!)/((n−1)!))) = (3/5) → (((2n+1)!(n−1)!)/((2n−1)!(n+2)!)) = (3/5) (((2n+1).2n.(n−1)!)/((n+2)(n+1)n(n−1)!)) = (3/5) ((4n+2)/((n+2)(n+1))) = (3/5) 20n+10 = 3(n^2 +3n+2) 3n^2 −11n−4 = 0 (3n+1)(n−4) = 0 → n=4

Answered by bemath last updated on 24/Sep/20

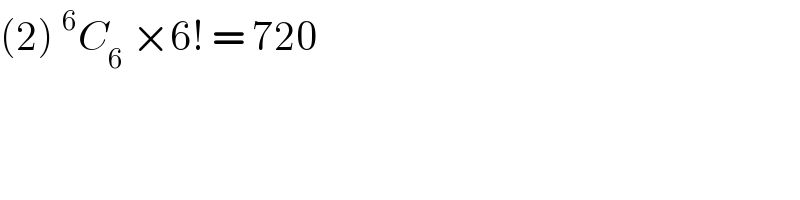
(2) ^6 C_6 ×6! = 720

Answered by bemath last updated on 24/Sep/20

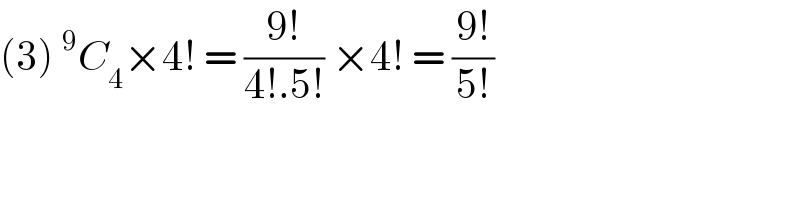
(3) ^9 C_4 ×4! = ((9!)/(4!.5!)) ×4! = ((9!)/(5!))