Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 115174 by bemath last updated on 24/Sep/20

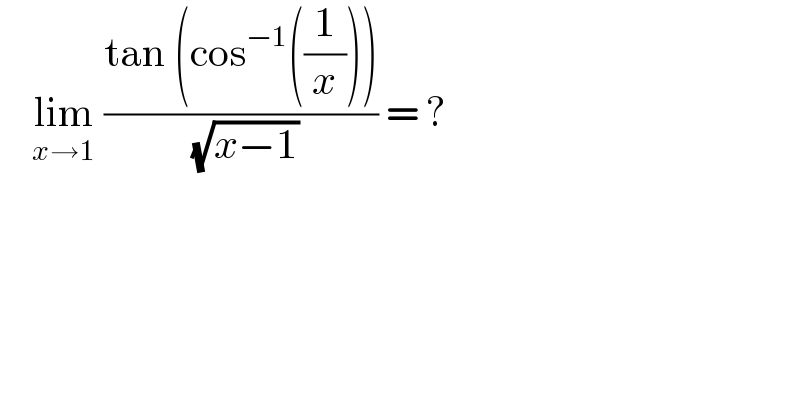
lim_(x→1) ((tan (cos^(−1) ((1/x))))/( (√(x−1)))) = ?

$$\:\:\:\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:\left(\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{x}}\right)\right)}{\:\sqrt{{x}−\mathrm{1}}}\:=\:? \\ $$

Answered by bobhans last updated on 24/Sep/20

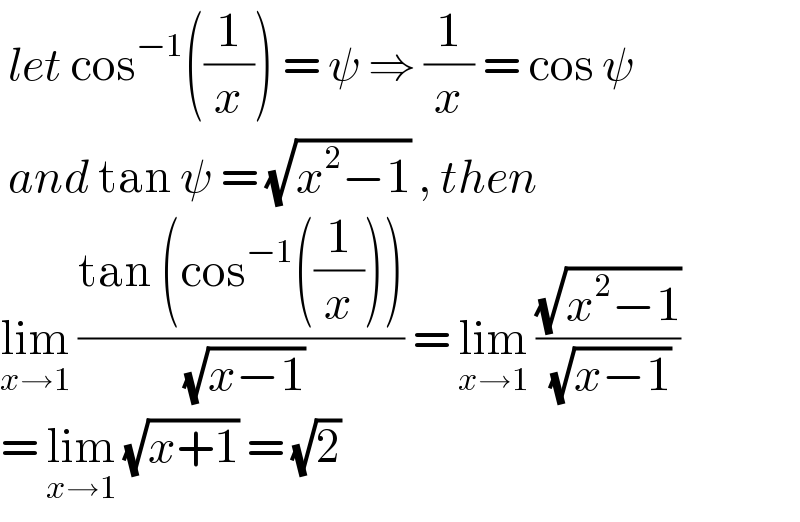
let cos^(−1) ((1/x)) = ψ ⇒ (1/x) = cos ψ and tan ψ = (√(x^2 −1)) , then lim_(x→1) ((tan (cos^(−1) ((1/x))))/( (√(x−1)))) = lim_(x→1) ((√(x^2 −1))/( (√(x−1)))) = lim_(x→1) (√(x+1)) = (√2)

$$\:{let}\:\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{x}}\right)\:=\:\psi\:\Rightarrow\:\frac{\mathrm{1}}{{x}}\:=\:\mathrm{cos}\:\psi\: \\ $$$$\:{and}\:\mathrm{tan}\:\psi\:=\:\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:,\:{then}\: \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{tan}\:\left(\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{x}}\right)\right)}{\:\sqrt{{x}−\mathrm{1}}}\:=\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{\:\sqrt{{x}−\mathrm{1}}}\: \\ $$$$=\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\sqrt{{x}+\mathrm{1}}\:=\:\sqrt{\mathrm{2}}\: \\ $$

Answered by Olaf last updated on 24/Sep/20

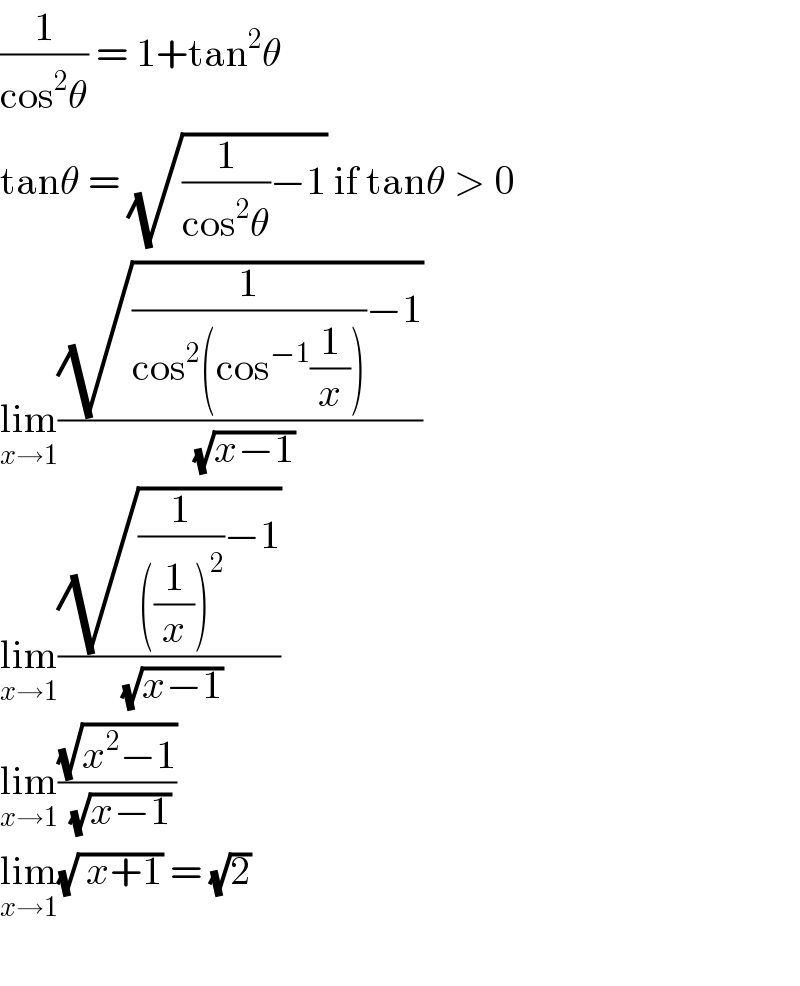
(1/(cos^2 θ)) = 1+tan^2 θ tanθ = (√((1/(cos^2 θ))−1)) if tanθ > 0 lim_(x→1) ((√((1/(cos^2 (cos^(−1) (1/x))))−1))/( (√(x−1)))) lim_(x→1) ((√((1/(((1/x))^2 ))−1))/( (√(x−1)))) lim_(x→1) ((√(x^2 −1))/( (√(x−1)))) lim_(x→1) (√( x+1)) = (√2)

$$\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \theta}\:=\:\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta \\ $$$$\mathrm{tan}\theta\:=\:\sqrt{\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \theta}−\mathrm{1}}\:\mathrm{if}\:\mathrm{tan}\theta\:>\:\mathrm{0} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\sqrt{\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \left(\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{{x}}\right)}−\mathrm{1}}}{\:\sqrt{{x}−\mathrm{1}}} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\sqrt{\frac{\mathrm{1}}{\left(\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} }−\mathrm{1}}}{\:\sqrt{{x}−\mathrm{1}}} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{\:\sqrt{{x}−\mathrm{1}}} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\sqrt{\:{x}+\mathrm{1}}\:=\:\sqrt{\mathrm{2}} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com