find the mean value of y=(5/(2−x−3x^2 )) between x=−(1/3) and x=(1/3)


Question and Answers Forum

All Questions Topic List
None Questions
Previous in All Question Next in All Question
Previous in None Next in None
Question Number 115229 by mathdave last updated on 24/Sep/20

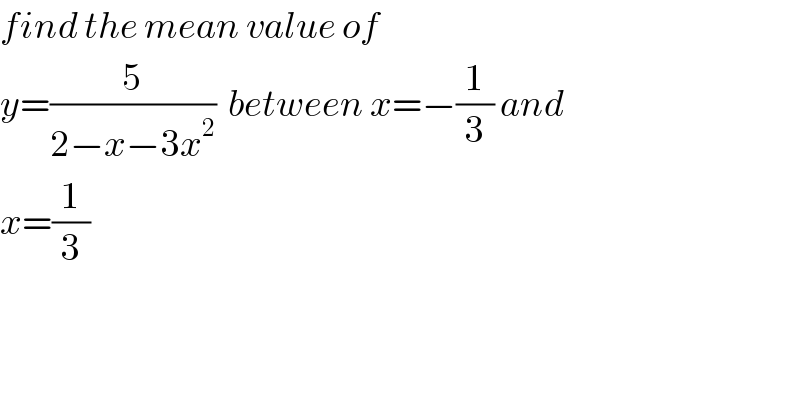
$f i n d t h e m e a n v a l u e o f$ $y = \frac{5}{2 - x - 3 x^{2}} b e t w e e n x = - \frac{1}{3} a n d$ $x = \frac{1}{3}$
	Answered by Olaf last updated on 24/Sep/20

	$\overline{y} = \frac{1}{\frac{1}{3} - (- \frac{1}{3})} \int_{- \frac{1}{3}}^{+ \frac{1}{3}} \frac{5}{2 - x - 3 x^{2}} d x$ $\overline{y} = - \frac{5}{2} \int_{- \frac{1}{3}}^{+ \frac{1}{3}} \frac{1}{x^{2} + \frac{1}{3} x - \frac{2}{3}} d x$ $\overline{y} = - \frac{5}{2} \int_{- \frac{1}{3}}^{+ \frac{1}{3}} \frac{1}{{(x + \frac{1}{6})}^{2} - \frac{25}{36}} d x$ $\overline{y} = - \frac{5}{2} \int_{- \frac{1}{3}}^{+ \frac{1}{3}} \frac{1}{\frac{25}{36} [{(\frac{6}{5} (x + \frac{1}{6}))}^{2} - 1]} d x$ $u = \frac{1}{5} (6 x + 1)$ $\overline{y} = - 3 \int_{- \frac{1}{5}}^{+ \frac{3}{5}} \frac{1}{u^{2} - 1} d u$ $\overline{y} = - 3 {[\frac{1}{2} \ln ∣ \frac{u - 1}{u + 1} ∣]}_{- \frac{1}{5}}^{\frac{3}{5}}$ $\overline{y} = - \frac{3}{2} [\ln ∣ \frac{- \frac{2}{5}}{\frac{8}{5}} ∣ - \ln ∣ \frac{- \frac{6}{5}}{\frac{4}{5}} ∣]$ $\overline{y} = - \frac{3}{2} [\ln (\frac{1}{4}) - \ln (\frac{3}{2})]$ $\overline{y} = - \frac{3}{2} \ln (\frac{1}{6})$ $\overline{y} = \frac{3}{2} \ln 6$
	Commented by mathdave last updated on 24/Sep/20

	$g u d w o r k$
	Answered by Bird last updated on 24/Sep/20
	$the mean value is (1/(b−a))∫_a ^b f(x)dx =(1/((1/3)−(−(1/3))))∫_(−(1/3)) ^(1/(3 )) (5/(−3x^2 −x+2))dx =−((15)/2) ∫_(−(1/3)) ^(1/3) (dx/(3x^2 +x−2)) Δ =1−4(−6) =25 ⇒x_1 =((−1+5)/6) =(2/3) and x_2 =((−1−5)/6) =−1 ⇒ M_f =−((15)/2) ∫_(−(1/3)) ^(1/3) (dx/(3(x−(2/3))(x+1))) =−(5/2)×(3/5) ∫_(−(1/3)) ^(1/3) ((1/(x−(2/3)))−(1/(x+1)))dx =−(3/2)[ln∣((x−(2/3))/(x+1))∣]_(−(1/3)) ^(1/3) =−(3/2){ln∣((−(1/3))/(4/3))∣−ln∣((−1)/(2/3))∣} =−(3/2){ln((3/4))−ln((3/2))} =−(3/2)ln((3/4)×(2/3)) =−(3/2)ln((1/2)) =((3ln(2))/2)$
	$t h e m e a n v a l u e i s \frac{1}{b - a} \int_{a}^{b} f (x) d x$ $= \frac{1}{\frac{1}{3} - (- \frac{1}{3})} \int_{- \frac{1}{3}}^{\frac{1}{3}} \frac{5}{- 3 x^{2} - x + 2} d x$ $= - \frac{15}{2} \int_{- \frac{1}{3}}^{\frac{1}{3}} \frac{d x}{3 x^{2} + x - 2}$ $Δ = 1 - 4 (- 6) = 25 \Rightarrow x_{1} = \frac{- 1 + 5}{6}$ $= \frac{2}{3} a n d x_{2} = \frac{- 1 - 5}{6} = - 1 \Rightarrow$ $M_{f} = - \frac{15}{2} \int_{- \frac{1}{3}}^{\frac{1}{3}} \frac{d x}{3 (x - \frac{2}{3}) (x + 1)}$ $= - \frac{5}{2} \times \frac{3}{5} \int_{- \frac{1}{3}}^{\frac{1}{3}} (\frac{1}{x - \frac{2}{3}} - \frac{1}{x + 1}) d x$ $= - \frac{3}{2} {[l n ∣ \frac{x - \frac{2}{3}}{x + 1} ∣]}_{- \frac{1}{3}}^{\frac{1}{3}}$ $= - \frac{3}{2} {l n ∣ \frac{- \frac{1}{3}}{\frac{4}{3}} ∣ - l n ∣ \frac{- 1}{\frac{2}{3}} ∣}$ $= - \frac{3}{2} {l n (\frac{3}{4}) - l n (\frac{3}{2})}$ $= - \frac{3}{2} l n (\frac{3}{4} \times \frac{2}{3}) = - \frac{3}{2} l n (\frac{1}{2})$ $= \frac{3 l n (2)}{2}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum