
Question Number 115273 by mnjuly1970 last updated on 24/Sep/20
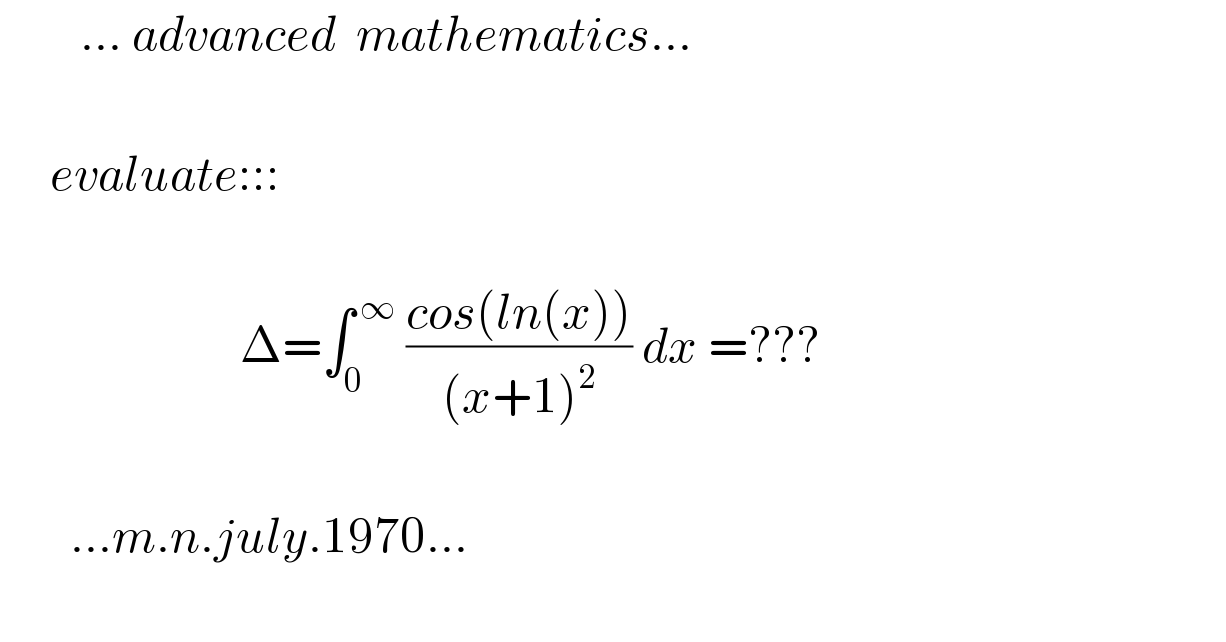
$$\:\:\:\:\:\:\:\:...\:{advanced}\:\:{mathematics}... \\ $$$$ \\ $$$$\:\:\:\:\:{evaluate}::: \\ $$$$\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Delta=\int_{\mathrm{0}} ^{\:\infty} \:\frac{{cos}\left({ln}\left({x}\right)\right)}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }\:{dx}\:=??? \\ $$$$ \\ $$$$\:\:\:\:\:\:\:...{m}.{n}.{july}.\mathrm{1970}... \\ $$$$\: \\ $$
Answered by Bird last updated on 24/Sep/20
![A =∫_0 ^∞ ((cos(lnx))/((x+1)^2 ))dx⇒ A =∫_0 ^1 ((cos(lnx))/((x+1)^2 ))dx +∫_1 ^∞ ((cos(lnx))/((x+1)^2 ))dx but ∫_1 ^∞ ((cos(lnx))/((x+1)^2 ))dx=_(x=(1/t)) −∫_0 ^1 ((cos(lnt))/(((1/t)+1)^2 ))(−(dt/t^2 )) =∫_0 ^1 ((cos(lnx))/((x+1)^2 )) ⇒A =2∫_0 ^(1 ) ((cos(lnx))/((x+1)^2 ))dx we have (1/(x+1)) =Σ_(n=0) ^∞ (−1)^n x^n ⇒−(1/((x+1)^2 )) =Σ_(n=1) ^∞ (−1)^n nx^(n−1) ⇒(1/((x+1)^2 )) =Σ_(n=1) ^∞ (−1)^(n−1) nx^(n−1) =Σ_(n=0) ^∞ (−1)^n (n+1)x^(n ) ⇒ A =2∫_0 ^1 Σ_(n=0) ^∞ (−1)^n (n+1)x^n cos(lnx)dx =2 Σ_(n=0) ^∞ (−1)^n (n+1)∫_0 ^(1 ) x^n cos(lnx)dx U_n =∫_0 ^(1 ) x^n cos(lnx)dx =_(lnx=−t) −∫_0 ^∞ e^(−nt) cos(t)(−e^(−t) )dt =∫_0 ^∞ e^(−(n+1)t) cos(t)dt =Re(∫_0 ^∞ e^(−(n+1)t) e^(it) dt) but ∫_0 ^∞ e^((−(n+1)+i)t) dt =[(1/(−(n+1)+i)) e^((−(n+1)+i)t) ]_0 ^∞ =(1/(n+1−i)) =((n+1+i)/((n+1)^2 +1)) ⇒ U_n =((n+1)/((n+1)^2 +1)) ⇒ A =2Σ_(n=0) ^∞ (−1)^n (n+1)×((n+1)/((n+1)^2 +1)) =Σ_(n=0) ^∞ (−1)^n (((n+1)^2 )/((n+1)^2 +1)) =Σ_(n=1) ^∞ (−1)^(n−1) .(n^2 /(n^2 +1)) =Σ_(n=1) ^∞ (−1)^(n−1) (1−(1/(n^2 +1))) =Σ_(n=1) ^∞ (−1)^(n−1) (→diverges)+Σ_(n=1) ^∞ (((−1)^n )/(n^2 +1))(converges) perhsps this integral is divergent..!](Q115289.png)
$${A}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{cos}\left({lnx}\right)}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}\Rightarrow \\ $$$${A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{cos}\left({lnx}\right)}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}\:+\int_{\mathrm{1}} ^{\infty} \:\frac{{cos}\left({lnx}\right)}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$${but}\:\int_{\mathrm{1}} ^{\infty} \:\frac{{cos}\left({lnx}\right)}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}=_{{x}=\frac{\mathrm{1}}{{t}}} \\ $$$$−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{cos}\left({lnt}\right)}{\left(\frac{\mathrm{1}}{{t}}+\mathrm{1}\right)^{\mathrm{2}} }\left(−\frac{{dt}}{{t}^{\mathrm{2}} }\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{cos}\left({lnx}\right)}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow{A}\:=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}\:} \frac{{cos}\left({lnx}\right)}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$${we}\:{have}\:\frac{\mathrm{1}}{{x}+\mathrm{1}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:{x}^{{n}} \\ $$$$\Rightarrow−\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }\:=\sum_{{n}=\mathrm{1}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {nx}^{{n}−\mathrm{1}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }\:=\sum_{{n}=\mathrm{1}} ^{\infty} \left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {nx}^{{n}−\mathrm{1}} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \left({n}+\mathrm{1}\right){x}^{{n}\:} \:\Rightarrow \\ $$$${A}\:=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \left({n}+\mathrm{1}\right){x}^{{n}} \:{cos}\left({lnx}\right){dx} \\ $$$$=\mathrm{2}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \left({n}+\mathrm{1}\right)\int_{\mathrm{0}} ^{\mathrm{1}\:} {x}^{{n}} {cos}\left({lnx}\right){dx} \\ $$$${U}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}\:} \:{x}^{{n}} \:{cos}\left({lnx}\right){dx} \\ $$$$=_{{lnx}=−{t}} \:\:\:−\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{nt}} \:{cos}\left({t}\right)\left(−{e}^{−{t}} \right){dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {e}^{−\left({n}+\mathrm{1}\right){t}} \:{cos}\left({t}\right){dt} \\ $$$$={Re}\left(\int_{\mathrm{0}} ^{\infty} \:{e}^{−\left({n}+\mathrm{1}\right){t}} \:{e}^{{it}} {dt}\right)\:{but} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{\left(−\left({n}+\mathrm{1}\right)+{i}\right){t}} \:{dt} \\ $$$$=\left[\frac{\mathrm{1}}{−\left({n}+\mathrm{1}\right)+{i}}\:{e}^{\left(−\left({n}+\mathrm{1}\right)+{i}\right){t}} \right]_{\mathrm{0}} ^{\infty} \\ $$$$=\frac{\mathrm{1}}{{n}+\mathrm{1}−{i}}\:\:=\frac{{n}+\mathrm{1}+{i}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$${U}_{{n}} =\frac{{n}+\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$${A}\:=\mathrm{2}\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \left({n}+\mathrm{1}\right)×\frac{{n}+\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:\:\:\:\frac{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }{\left({n}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} .\frac{{n}^{\mathrm{2}} }{{n}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left(\mathrm{1}−\frac{\mathrm{1}}{{n}^{\mathrm{2}} \:+\mathrm{1}}\right) \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left(\rightarrow{diverges}\right)+\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} +\mathrm{1}}\left({converges}\right) \\ $$$${perhsps}\:{this}\:{integral}\:{is}\:{divergent}..! \\ $$
Commented by mnjuly1970 last updated on 24/Sep/20

Commented by mnjuly1970 last updated on 24/Sep/20
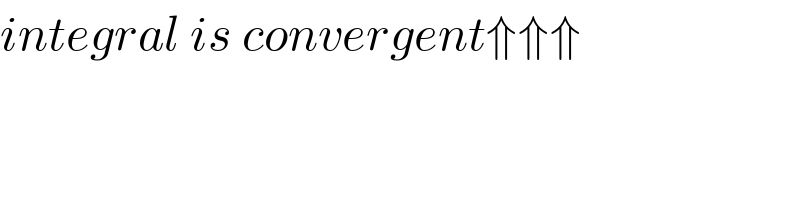
$${integral}\:{is}\:{convergent}\Uparrow\Uparrow\Uparrow \\ $$
Commented by Dwaipayan Shikari last updated on 24/Sep/20
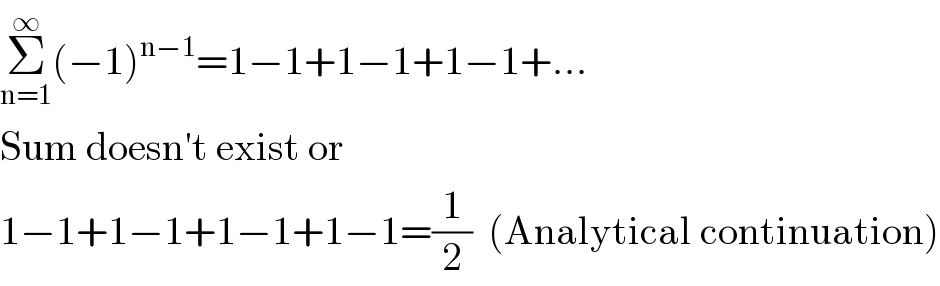
$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} =\mathrm{1}−\mathrm{1}+\mathrm{1}−\mathrm{1}+\mathrm{1}−\mathrm{1}+... \\ $$$$\mathrm{Sum}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exist}\:\mathrm{or} \\ $$$$\mathrm{1}−\mathrm{1}+\mathrm{1}−\mathrm{1}+\mathrm{1}−\mathrm{1}+\mathrm{1}−\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}}\:\:\left(\mathrm{Analytical}\:\mathrm{continuation}\right) \\ $$
Commented by Olaf last updated on 24/Sep/20
![U_n = ∫_0 ^1 x^n cos(lnx)dx = ∫_0 ^1 x^(n+1) ((cos(lnx))/x)dx U_n = [x^(n+1) sin(lnx)]_0 ^1 − ∫_0 ^1 (n+1)x^n sin(lnx)dx U_n = −(n+1) ∫_0 ^1 x^(n+1) ((sin(lnx))/x)dx U_n = −(n+1){ [−x^(n+1) cos(lnx)]_0 ^1 +(n+1)∫_0 ^1 x^n cos(lnx)dx} U_n = −(n+1)(−1+(n+1)U_n ) (1+(n+1)^2 )U_n = n+1 U_n = ((n+1)/((n+1)^2 +1)) maybe...](Q115299.png)
$$\mathrm{U}_{{n}} \:=\:\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} \mathrm{cos}\left(\mathrm{ln}{x}\right){dx}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}+\mathrm{1}} \frac{\mathrm{cos}\left(\mathrm{ln}{x}\right)}{{x}}{dx} \\ $$$$\mathrm{U}_{{n}} \:=\:\left[{x}^{{n}+\mathrm{1}} \mathrm{sin}\left(\mathrm{ln}{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\:\int_{\mathrm{0}} ^{\mathrm{1}} \left({n}+\mathrm{1}\right){x}^{{n}} \mathrm{sin}\left(\mathrm{ln}{x}\right){dx} \\ $$$$\mathrm{U}_{{n}} \:=\:−\left({n}+\mathrm{1}\right)\:\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}+\mathrm{1}} \frac{\mathrm{sin}\left(\mathrm{ln}{x}\right)}{{x}}{dx} \\ $$$$\mathrm{U}_{{n}} \:=\:−\left({n}+\mathrm{1}\right)\left\{\:\left[−{x}^{{n}+\mathrm{1}} \mathrm{cos}\left(\mathrm{ln}{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\left({n}+\mathrm{1}\right)\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} \mathrm{cos}\left(\mathrm{ln}{x}\right){dx}\right\} \\ $$$$\mathrm{U}_{{n}} \:=\:−\left({n}+\mathrm{1}\right)\left(−\mathrm{1}+\left({n}+\mathrm{1}\right)\mathrm{U}_{{n}} \right) \\ $$$$\left(\mathrm{1}+\left({n}+\mathrm{1}\right)^{\mathrm{2}} \right)\mathrm{U}_{{n}} \:=\:{n}+\mathrm{1} \\ $$$$\mathrm{U}_{{n}} \:=\:\frac{{n}+\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$$${maybe}... \\ $$$$ \\ $$
Commented by Bird last updated on 24/Sep/20
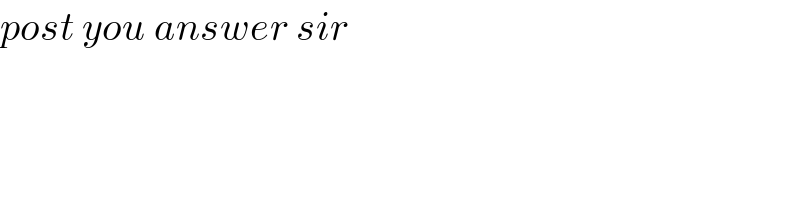
$${post}\:{you}\:{answer}\:{sir} \\ $$
Commented by mnjuly1970 last updated on 24/Sep/20
$$\:{ok}\:.{i}\:{sent}\:{my}\:{solution}. \\ $$
Commented by mnjuly1970 last updated on 24/Sep/20

Commented by Bird last updated on 25/Sep/20

$${ok}\:{thanks} \\ $$
Answered by mnjuly1970 last updated on 24/Sep/20
![solution Δ =Re∫_0 ^( ∞) (e^(iln(x)) /((x+1)^2 ))dx=Re∫_0 ^( ∞) (x^i /((x+1)^2 ))dx =Re∫_0 ^( ∞) (x^((i+1)−1) /((x+1)^2 ))dx=Re(β(1+i , 1−i)) =Re((Γ(1+i)Γ(1−i))/(⟨Γ(2)=1⟩))= Re[iΓ(i)Γ(1−i)]=^(euler reflection formula) Re[i(π/(sin(iπ))] =Re[((2i(iπ))/(e^(i(iπ)) −e^(−i(iπ)) ))]=((−2π)/(e^(−π) −e^π )) =(π/((e^π −e^(−π) )/2))=(π/(sinh(π))) ✓ m.n.july. 1970](Q115304.png)
$$\:{solution} \\ $$$$\:\Delta\:=\mathscr{R}{e}\int_{\mathrm{0}} ^{\:\infty} \frac{{e}^{{iln}\left({x}\right)} }{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}=\mathscr{R}{e}\int_{\mathrm{0}} ^{\:\infty} \frac{{x}^{{i}} }{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}\:\:\:\:\: \\ $$$$=\mathscr{R}{e}\int_{\mathrm{0}} ^{\:\infty} \frac{{x}^{\left({i}+\mathrm{1}\right)−\mathrm{1}} }{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}=\mathscr{R}{e}\left(\beta\left(\mathrm{1}+{i}\:,\:\mathrm{1}−{i}\right)\right) \\ $$$$=\mathscr{R}{e}\frac{\Gamma\left(\mathrm{1}+{i}\right)\Gamma\left(\mathrm{1}−{i}\right)}{\langle\Gamma\left(\mathrm{2}\right)=\mathrm{1}\rangle}= \\ $$$$\:\:\mathscr{R}{e}\left[{i}\Gamma\left({i}\right)\Gamma\left(\mathrm{1}−{i}\right)\right]\overset{{euler}\:{reflection}\:\:{formula}} {=}\mathscr{R}{e}\left[{i}\frac{\pi}{{sin}\left({i}\pi\right.}\right] \\ $$$$=\mathscr{R}{e}\left[\frac{\mathrm{2}{i}\left({i}\pi\right)}{{e}^{{i}\left({i}\pi\right)} −{e}^{−{i}\left({i}\pi\right)} }\right]=\frac{−\mathrm{2}\pi}{{e}^{−\pi} −{e}^{\pi} } \\ $$$$=\frac{\pi}{\frac{{e}^{\pi} −{e}^{−\pi} }{\mathrm{2}}}=\frac{\pi}{{sinh}\left(\pi\right)}\:\:\checkmark \\ $$$$\:{m}.{n}.{july}.\:\mathrm{1970} \\ $$$$\:\:\:\: \\ $$
