Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 115417 by toa last updated on 25/Sep/20

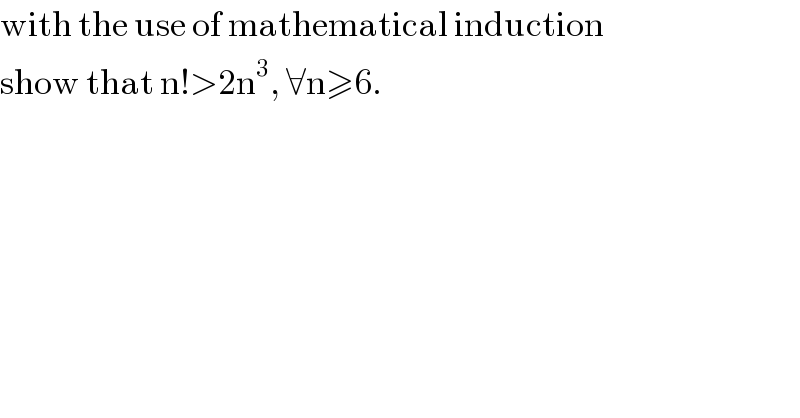
with the use of mathematical induction show that n!>2n^3 , ∀n≥6.

$$\mathrm{with}\:\mathrm{the}\:\mathrm{use}\:\mathrm{of}\:\mathrm{mathematical}\:\mathrm{induction} \\ $$ $$\mathrm{show}\:\mathrm{that}\:\mathrm{n}!>\mathrm{2n}^{\mathrm{3}} ,\:\forall\mathrm{n}\geqslant\mathrm{6}. \\ $$

Answered by TANMAY PANACEA last updated on 25/Sep/20

when n=6 6!=720 2×6^3 =432 n!>2n^3 when n=6 let when n=p, the given statment is true p!>2p^3 we have to prove that (p+1)!>2(p+1)^3 now (p+1)p!−2(p+1)^3 (p+1){p!−2(p+1)^2 } let assume p!=2p^3 +δ→δ is positive value (p+1){2p^3 +δ−2(p+1)^2 } (p+1)[2{(p^3 −(p+1)^2 }+δ] →is positive because when p≥6 p^3 >(p+1)^2 pls check

$${when}\:{n}=\mathrm{6} \\ $$ $$\mathrm{6}!=\mathrm{720}\:\:\:\:\mathrm{2}×\mathrm{6}^{\mathrm{3}} =\mathrm{432}\:\:\:{n}!>\mathrm{2}{n}^{\mathrm{3}} \:\:{when}\:{n}=\mathrm{6} \\ $$ $${let}\:{when}\:{n}={p},\:{the}\:{given}\:{statment}\:{is}\:{true} \\ $$ $${p}!>\mathrm{2}{p}^{\mathrm{3}} \\ $$ $${we}\:{have}\:{to}\:{prove}\:{that} \\ $$ $$\left({p}+\mathrm{1}\right)!>\mathrm{2}\left({p}+\mathrm{1}\right)^{\mathrm{3}} \\ $$ $${now} \\ $$ $$\left({p}+\mathrm{1}\right){p}!−\mathrm{2}\left({p}+\mathrm{1}\right)^{\mathrm{3}} \\ $$ $$\left({p}+\mathrm{1}\right)\left\{{p}!−\mathrm{2}\left({p}+\mathrm{1}\right)^{\mathrm{2}} \right\} \\ $$ $${let}\:{assume}\:{p}!=\mathrm{2}{p}^{\mathrm{3}} +\delta\rightarrow\delta\:{is}\:{positive}\:{value} \\ $$ $$\left({p}+\mathrm{1}\right)\left\{\mathrm{2}{p}^{\mathrm{3}} +\delta−\mathrm{2}\left({p}+\mathrm{1}\right)^{\mathrm{2}} \right\} \\ $$ $$\left({p}+\mathrm{1}\right)\left[\mathrm{2}\left\{\left({p}^{\mathrm{3}} −\left({p}+\mathrm{1}\right)^{\mathrm{2}} \right\}+\delta\right]\:\rightarrow{is}\:{positive}\right. \\ $$ $${because}\:{when}\:{p}\geqslant\mathrm{6} \\ $$ $${p}^{\mathrm{3}} >\left({p}+\mathrm{1}\right)^{\mathrm{2}} \:\:\:\:{pls}\:{check} \\ $$ $$ \\ $$

Answered by MWSuSon last updated on 25/Sep/20

Base case(n=6): 6!=720>2×6^3 =432 Inductive step{Goal: (n+1)!>2(n+1)^3 } suppose k≥6 and k!>2k^3 Observe that (k+1)!=(k+1)k! >(k+1)2k^3 =k(2k^3 )+2k^3 =k(2k^3 )+(k^3 +k^3 ) (observe that ∀ k≥6, k^3 ≥6k^2 >6k+2) >k(2k^3 )+(6k^2 +6k+2) >2k^3 +6k^2 +6k+2 =2(k+1)^3 Therefore n!>2n^3 (verify if this is logical)

$$\mathrm{Base}\:\mathrm{case}\left(\mathrm{n}=\mathrm{6}\right):\:\mathrm{6}!=\mathrm{720}>\mathrm{2}×\mathrm{6}^{\mathrm{3}} =\mathrm{432} \\ $$ $$\mathrm{Inductive}\:\mathrm{step}\left\{\mathrm{Goal}:\:\left(\mathrm{n}+\mathrm{1}\right)!>\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{3}} \right\} \\ $$ $$\mathrm{suppose}\:\mathrm{k}\geqslant\mathrm{6}\:\mathrm{and}\:\mathrm{k}!>\mathrm{2k}^{\mathrm{3}} \\ $$ $$\mathrm{Observe}\:\mathrm{that}\:\left(\mathrm{k}+\mathrm{1}\right)!=\left(\mathrm{k}+\mathrm{1}\right)\mathrm{k}! \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:>\left(\mathrm{k}+\mathrm{1}\right)\mathrm{2k}^{\mathrm{3}} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{k}\left(\mathrm{2k}^{\mathrm{3}} \right)+\mathrm{2k}^{\mathrm{3}} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{k}\left(\mathrm{2k}^{\mathrm{3}} \right)+\left(\mathrm{k}^{\mathrm{3}} +\mathrm{k}^{\mathrm{3}} \right)\: \\ $$ $$\left(\mathrm{observe}\:\mathrm{that}\:\forall\:\mathrm{k}\geqslant\mathrm{6},\:\mathrm{k}^{\mathrm{3}} \geqslant\mathrm{6k}^{\mathrm{2}} >\mathrm{6k}+\mathrm{2}\right) \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:>\mathrm{k}\left(\mathrm{2k}^{\mathrm{3}} \right)+\left(\mathrm{6k}^{\mathrm{2}} +\mathrm{6k}+\mathrm{2}\right) \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:>\mathrm{2k}^{\mathrm{3}} +\mathrm{6k}^{\mathrm{2}} +\mathrm{6k}+\mathrm{2} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{3}} \\ $$ $$\mathrm{Therefore}\:\mathrm{n}!>\mathrm{2n}^{\mathrm{3}} \\ $$ $$ \\ $$ $$\left(\mathrm{verify}\:\mathrm{if}\:\mathrm{this}\:\mathrm{is}\:\mathrm{logical}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com