
Question Number 115761 by mnjuly1970 last updated on 28/Sep/20
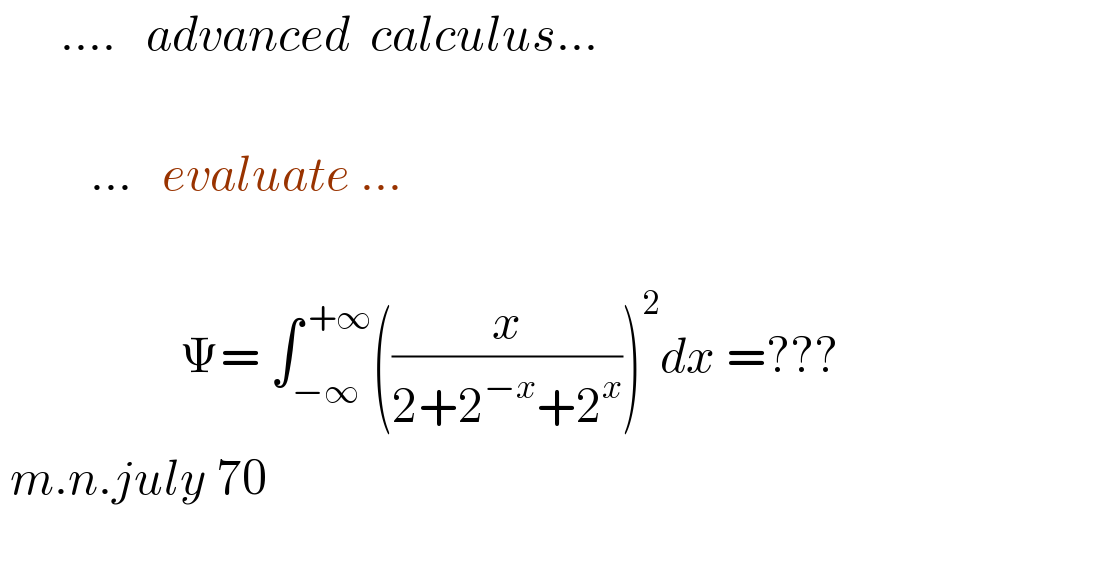
$$\:\:\:\:\:\:....\:\:\:{advanced}\:\:{calculus}...\: \\ $$$$\: \\ $$$$\:\:\:\:\:\:\:\:\:...\:\:\:{evaluate}\:...\: \\ $$$$\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Psi=\:\int_{−\infty} ^{\:+\infty} \left(\frac{{x}}{\mathrm{2}+\mathrm{2}^{−{x}} +\mathrm{2}^{{x}} }\right)^{\mathrm{2}} {dx}\:=??? \\ $$$$\:{m}.{n}.{july}\:\mathrm{70} \\ $$$$ \\ $$
Commented by Olaf last updated on 28/Sep/20
![Ψ = 2∫_0 ^∞ ((x/(2+2^(−x) +2^x )))^2 dx u = 2^x = e^(xln2) du = ln2.e^(xln2) dx ⇒ dx = (du/(uln2)) Ψ = 2∫_1 ^∞ ((((lnu)/(ln2))/(2+(1/u)+u)))^2 (du/(uln2)) Ψ = (2/(ln^3 2))∫_1 ^∞ u(((lnu)/(u^2 +2u+1)))^2 du Ψ = (2/(ln^3 2))∫_1 ^∞ u((ln^2 u)/((u+1)^4 ))du (u/((u+1)^4 )) = (1/((u+1)^3 ))−(1/((u+1)^4 )) Ψ = (2/(ln^3 2))[(−(1/(2(u+1)^2 ))+(1/(3(u+1)^3 )))ln^2 u]_1 ^∞ − (2/(ln^3 2))∫_1 ^∞ (−(1/(2(u+1)^2 ))+(1/(3(u+1)^3 )))2((lnu)/u) Ψ = (2/(ln^3 2))∫_1 ^∞ ((lnu)/(u(u+1)^2 ))du−(4/(3ln^3 2))∫_1 ^∞ ((lnu)/(u(u+1)^3 ))du I = ∫_1 ^∞ ((lnu)/(u(u+1)^2 ))du J = ∫_1 ^∞ ((lnu)/(u(u+1)^3 ))du (1/(u(u+1)^2 )) = (1/u)−(1/(1+u))−(1/((1+u)^2 )) (1/(u(u+1)^3 )) = (1/u)−(1/(1+u))−(1/((1+u)^2 ))−(1/((1+u)^3 )) Ψ = (2/(ln^3 2))I−(4/(3ln^3 2))J Ψ = (2/(3ln^3 2))[∫_1 ^∞ ((lnu)/u)du−∫_1 ^∞ ((lnu)/(1+u))du−∫_1 ^∞ ((lnu)/((1+u)^2 ))du]−(4/(3ln^3 2))∫_1 ^∞ ((lnu)/((1+u)^3 ))du A_0 = ∫_1 ^∞ ((lnu)/u)du = ∞... ? ... it′s probably false. I tried.](Q115786.png)
$$ \\ $$$$\Psi\:=\:\mathrm{2}\int_{\mathrm{0}} ^{\infty} \left(\frac{{x}}{\mathrm{2}+\mathrm{2}^{−{x}} +\mathrm{2}^{{x}} }\right)^{\mathrm{2}} {dx} \\ $$$${u}\:=\:\mathrm{2}^{{x}} \:=\:{e}^{{x}\mathrm{ln2}} \\ $$$${du}\:=\:\mathrm{ln2}.{e}^{{x}\mathrm{ln2}} {dx}\:\Rightarrow\:{dx}\:=\:\frac{{du}}{{u}\mathrm{ln2}} \\ $$$$\Psi\:=\:\mathrm{2}\int_{\mathrm{1}} ^{\infty} \left(\frac{\frac{\mathrm{ln}{u}}{\mathrm{ln2}}}{\mathrm{2}+\frac{\mathrm{1}}{{u}}+{u}}\right)^{\mathrm{2}} \frac{{du}}{{u}\mathrm{ln2}} \\ $$$$\Psi\:=\:\frac{\mathrm{2}}{\mathrm{ln}^{\mathrm{3}} \mathrm{2}}\int_{\mathrm{1}} ^{\infty} {u}\left(\frac{\mathrm{ln}{u}}{{u}^{\mathrm{2}} +\mathrm{2}{u}+\mathrm{1}}\right)^{\mathrm{2}} {du} \\ $$$$\Psi\:=\:\frac{\mathrm{2}}{\mathrm{ln}^{\mathrm{3}} \mathrm{2}}\int_{\mathrm{1}} ^{\infty} {u}\frac{\mathrm{ln}^{\mathrm{2}} {u}}{\left({u}+\mathrm{1}\right)^{\mathrm{4}} }{du} \\ $$$$\frac{{u}}{\left({u}+\mathrm{1}\right)^{\mathrm{4}} }\:=\:\frac{\mathrm{1}}{\left({u}+\mathrm{1}\right)^{\mathrm{3}} }−\frac{\mathrm{1}}{\left({u}+\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$\Psi\:=\:\frac{\mathrm{2}}{\mathrm{ln}^{\mathrm{3}} \mathrm{2}}\left[\left(−\frac{\mathrm{1}}{\mathrm{2}\left({u}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}\left({u}+\mathrm{1}\right)^{\mathrm{3}} }\right)\mathrm{ln}^{\mathrm{2}} {u}\right]_{\mathrm{1}} ^{\infty} \\ $$$$−\:\frac{\mathrm{2}}{\mathrm{ln}^{\mathrm{3}} \mathrm{2}}\int_{\mathrm{1}} ^{\infty} \left(−\frac{\mathrm{1}}{\mathrm{2}\left({u}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}\left({u}+\mathrm{1}\right)^{\mathrm{3}} }\right)\mathrm{2}\frac{\mathrm{ln}{u}}{{u}} \\ $$$$\Psi\:=\:\:\frac{\mathrm{2}}{\mathrm{ln}^{\mathrm{3}} \mathrm{2}}\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{ln}{u}}{{u}\left({u}+\mathrm{1}\right)^{\mathrm{2}} }{du}−\frac{\mathrm{4}}{\mathrm{3ln}^{\mathrm{3}} \mathrm{2}}\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{ln}{u}}{{u}\left({u}+\mathrm{1}\right)^{\mathrm{3}} }{du} \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{ln}{u}}{{u}\left({u}+\mathrm{1}\right)^{\mathrm{2}} }{du} \\ $$$$\mathrm{J}\:=\:\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{ln}{u}}{{u}\left({u}+\mathrm{1}\right)^{\mathrm{3}} }{du} \\ $$$$\frac{\mathrm{1}}{{u}\left({u}+\mathrm{1}\right)^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{{u}}−\frac{\mathrm{1}}{\mathrm{1}+{u}}−\frac{\mathrm{1}}{\left(\mathrm{1}+{u}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{{u}\left({u}+\mathrm{1}\right)^{\mathrm{3}} }\:=\:\frac{\mathrm{1}}{{u}}−\frac{\mathrm{1}}{\mathrm{1}+{u}}−\frac{\mathrm{1}}{\left(\mathrm{1}+{u}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left(\mathrm{1}+{u}\right)^{\mathrm{3}} } \\ $$$$\Psi\:=\:\frac{\mathrm{2}}{\mathrm{ln}^{\mathrm{3}} \mathrm{2}}\mathrm{I}−\frac{\mathrm{4}}{\mathrm{3ln}^{\mathrm{3}} \mathrm{2}}\mathrm{J} \\ $$$$\Psi\:=\:\frac{\mathrm{2}}{\mathrm{3ln}^{\mathrm{3}} \mathrm{2}}\left[\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{ln}{u}}{{u}}{du}−\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{ln}{u}}{\mathrm{1}+{u}}{du}−\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{ln}{u}}{\left(\mathrm{1}+{u}\right)^{\mathrm{2}} }{du}\right]−\frac{\mathrm{4}}{\mathrm{3ln}^{\mathrm{3}} \mathrm{2}}\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{ln}{u}}{\left(\mathrm{1}+{u}\right)^{\mathrm{3}} }{du} \\ $$$$\mathrm{A}_{\mathrm{0}} \:=\:\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{ln}{u}}{{u}}{du}\:=\:\infty...\:? \\ $$$$...\:\mathrm{it}'\mathrm{s}\:\mathrm{probably}\:\mathrm{false}.\:\mathrm{I}\:\mathrm{tried}. \\ $$
Answered by MJS_new last updated on 28/Sep/20
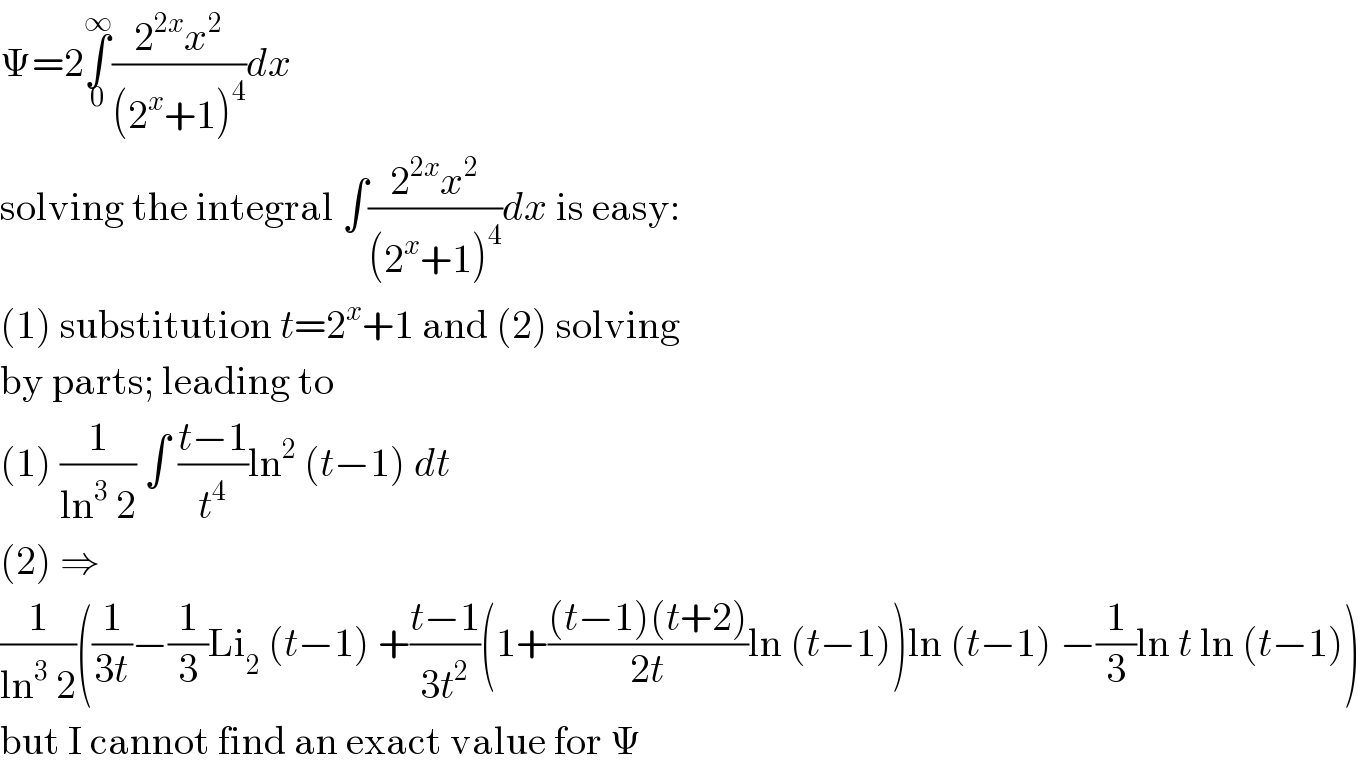
$$\Psi=\mathrm{2}\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{\mathrm{2}^{\mathrm{2}{x}} {x}^{\mathrm{2}} }{\left(\mathrm{2}^{{x}} +\mathrm{1}\right)^{\mathrm{4}} }{dx} \\ $$$$\mathrm{solving}\:\mathrm{the}\:\mathrm{integral}\:\int\frac{\mathrm{2}^{\mathrm{2}{x}} {x}^{\mathrm{2}} }{\left(\mathrm{2}^{{x}} +\mathrm{1}\right)^{\mathrm{4}} }{dx}\:\mathrm{is}\:\mathrm{easy}: \\ $$$$\left(\mathrm{1}\right)\:\mathrm{substitution}\:{t}=\mathrm{2}^{{x}} +\mathrm{1}\:\mathrm{and}\:\left(\mathrm{2}\right)\:\mathrm{solving} \\ $$$$\mathrm{by}\:\mathrm{parts};\:\mathrm{leading}\:\mathrm{to} \\ $$$$\left(\mathrm{1}\right)\:\frac{\mathrm{1}}{\mathrm{ln}^{\mathrm{3}} \:\mathrm{2}}\:\int\:\frac{{t}−\mathrm{1}}{{t}^{\mathrm{4}} }\mathrm{ln}^{\mathrm{2}} \:\left({t}−\mathrm{1}\right)\:{dt} \\ $$$$\left(\mathrm{2}\right)\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{ln}^{\mathrm{3}} \:\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{3}{t}}−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{Li}_{\mathrm{2}} \:\left({t}−\mathrm{1}\right)\:+\frac{{t}−\mathrm{1}}{\mathrm{3}{t}^{\mathrm{2}} }\left(\mathrm{1}+\frac{\left({t}−\mathrm{1}\right)\left({t}+\mathrm{2}\right)}{\mathrm{2}{t}}\mathrm{ln}\:\left({t}−\mathrm{1}\right)\right)\mathrm{ln}\:\left({t}−\mathrm{1}\right)\:−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:{t}\:\mathrm{ln}\:\left({t}−\mathrm{1}\right)\right) \\ $$$$\mathrm{but}\:\mathrm{I}\:\mathrm{cannot}\:\mathrm{find}\:\mathrm{an}\:\mathrm{exact}\:\mathrm{value}\:\mathrm{for}\:\Psi \\ $$
Commented by mnjuly1970 last updated on 29/Sep/20
$${very}\:{nice}\:{thank}\:{you} \\ $$$${master}... \\ $$
Answered by maths mind last updated on 29/Sep/20
![Ψ=2∫_0 ^∞ ((x^2 2^(2x) )/((1+2^(x+1) +2^(2x) )^2 ))dx =2∫_0 ^∞ ((2^(2x) x^2 )/((1+2^x )^4 )) let t=2^x ⇒x=((ln(t))/(ln(2))),dx=(dt/(tln(2))) =(2/(ln^3 (2)))∫_1 ^∞ ((tln^2 (t))/((1+t)^4 ))dt,t=(1/s) =(2/(ln^3 (2)))∫_0 ^1 ((sln^2 (s))/((1+s)^4 ))ds =(2/(ln^3 (2)))∫_0 ^1 (((ln^2 (s))/((1+s)^3 ))−((ln^2 (s))/((1+s)^4 )))ds=(2/(ln^3 (2)))[I−J] I=∫_0 ^1 ((ln^2 (s))/((1+s)^3 ))ds=lim_(x→0) [((−1)/(2(1+s)^2 ))ln^2 (s)]_x ^1 +∫_x ^1 ((ln(s))/(s(1+s)^2 ))ds =lim_(x→0) ((ln^2 (x))/(2(1+x)^2 ))+∫_x ^1 ((((1+s)^2 −s(1+s)−s))/(s(1+s)^2 )))ln(s)ds =lim_(x→0) ((ln^2 (x))/(2(1+x)^2 ))+∫_x ^1 ((ln(s))/s)ds−∫_0 ^1 ((ln(s))/(1+s))−∫_0 ^1 ((ln(s))/((s+1)^2 )) =lim_(x→0) ((1/(2(1+x)^2 ))−(1/2))ln^2 (x)−∫_0 ^1 Σ_(k≥0) (−1)^k s^k ln(s)ds −[[−((ln(s))/(1+s))]_x ^1 +∫_x ^1 (1/(s(s+1)))ds] =Σ_(k≥0) (−1)^k (1/((k+1)^2 ))−lim_(x→0) {((ln(x))/(1+x))+∫_x ^1 (1/s)ds−∫_x ^1 (1/(s+1))dx} I=(π^2 /(12))−lim_(x→0) {((ln(x))/(1+x))−ln(x)−ln(2)+ln(x+1)}=(π^2 /(12))+ln(2) J=∫_0 ^1 ((ln^2 (s))/((1+s)^4 ))ds =lim_(x→0) [−((ln^2 (s))/(3(1+s)^3 ))]_x ^1 +(2/3)∫_x ^1 ((ln(s))/(s(1+s)^3 ))ds] (1/(s(1+s)^3 ))=(((1+s)^3 −s(1+s)^2 −s(1+s)−s)/(s(1+s)^3 )) =lim_(x→0) ((ln^2 (x))/(3(1+x)^3 ))+(2/3)∫_x ^1 (((ln(s))/s)−((ln(s))/(1+s))−((ln(s))/((1+s)^2 ))−((ln(s))/((1+s)^3 ))) =lim_(x→0) (((ln^2 (x))/(3(1+x)^3 ))−((ln^2 (x))/3))_(=0) −(2/3)∫_0 ^1 ((ln(s))/(1+s))ds−(2/3)∫_0 ^1 ((ln(s))/((1+s)^2 ))−(2/3)∫_0 ^1 =−(2/3)Σ(((−1)^k )/((k+1)^2 ))−(2/3).−ln(2)−(2/3)lim_(x→0) {[((−ln(s))/(2(1+s)^2 ))]_x ^1 +∫_x ^1 (1/(2s(1+s)^2 ))} =(π^2 /(18))+((2ln(2))/3)−(2/3)lim_(x→0) [((ln(x))/(2(1+x)^2 ))+∫_x ^1 (((1+s)^2 −s(1+s)−s)/(2s(s+1)^2 ))ds =(π^2 /(18))+((2ln(2))/3)−(2/3)[((ln(x))/(2(1+x)^2 ))+∫_x ^1 (1/(2s))ds−(1/2)∫_0 ^1 (1/(1+s))−(1/2)∫_0 ^1 (1/((1+s)^2 ))] =(π^2 /(18))+((2ln(2))/3)−(2/3)lim_(x→0) {[((ln(x))/(2(1+x)^2 ))−((ln(x))/2)]_ −((ln(2))/2)+(1/2)((1/2)−1)]} =(π^2 /(18))+((2ln(2))/3)+((ln(2))/3)+(1/(16))=(π^2 /(18))+ln(2)+(1/6) Ψ=(2/(ln^3 (2)))[I−J]=(2/(ln^3 (2)))[(π^2 /(12))+ln(2)−((π^2 /(18))+ln(2)+(1/6))] =(2/(ln^3 (2)))[((π^2 −6)/(36))]=((π^2 −6)/(18ln^3 (2)))](Q115953.png)
$$\Psi=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{2}} \mathrm{2}^{\mathrm{2}{x}} }{\left(\mathrm{1}+\mathrm{2}^{{x}+\mathrm{1}} +\mathrm{2}^{\mathrm{2}{x}} \right)^{\mathrm{2}} }{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}^{\mathrm{2}{x}} {x}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{2}^{{x}} \right)^{\mathrm{4}} }\: \\ $$$${let}\:{t}=\mathrm{2}^{{x}} \Rightarrow{x}=\frac{{ln}\left({t}\right)}{{ln}\left(\mathrm{2}\right)},{dx}=\frac{{dt}}{{tln}\left(\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{2}}{{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}\int_{\mathrm{1}} ^{\infty} \frac{{tln}^{\mathrm{2}} \left({t}\right)}{\left(\mathrm{1}+{t}\right)^{\mathrm{4}} }{dt},{t}=\frac{\mathrm{1}}{{s}} \\ $$$$=\frac{\mathrm{2}}{{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{sln}^{\mathrm{2}} \left({s}\right)}{\left(\mathrm{1}+{s}\right)^{\mathrm{4}} }{ds} \\ $$$$=\frac{\mathrm{2}}{{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{{ln}^{\mathrm{2}} \left({s}\right)}{\left(\mathrm{1}+{s}\right)^{\mathrm{3}} }−\frac{{ln}^{\mathrm{2}} \left({s}\right)}{\left(\mathrm{1}+{s}\right)^{\mathrm{4}} }\right){ds}=\frac{\mathrm{2}}{{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}\left[{I}−{J}\right] \\ $$$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left({s}\right)}{\left(\mathrm{1}+{s}\right)^{\mathrm{3}} }{ds}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\frac{−\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+{s}\right)^{\mathrm{2}} }{ln}^{\mathrm{2}} \left({s}\right)\right]_{{x}} ^{\mathrm{1}} +\int_{{x}} ^{\mathrm{1}} \frac{{ln}\left({s}\right)}{{s}\left(\mathrm{1}+{s}\right)^{\mathrm{2}} }{ds} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{ln}^{\mathrm{2}} \left({x}\right)}{\mathrm{2}\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }+\int_{{x}} ^{\mathrm{1}} \left(\frac{\left.\left(\mathrm{1}+{s}\right)^{\mathrm{2}} −{s}\left(\mathrm{1}+{s}\right)−{s}\right)}{{s}\left(\mathrm{1}+{s}\right)^{\mathrm{2}} }\right){ln}\left({s}\right){ds} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{ln}^{\mathrm{2}} \left({x}\right)}{\mathrm{2}\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }+\int_{{x}} ^{\mathrm{1}} \frac{{ln}\left({s}\right)}{{s}}{ds}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({s}\right)}{\mathrm{1}+{s}}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({s}\right)}{\left({s}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}\right){ln}^{\mathrm{2}} \left({x}\right)−\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{k}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{k}} {s}^{{k}} {ln}\left({s}\right){ds} \\ $$$$−\left[\left[−\frac{{ln}\left({s}\right)}{\mathrm{1}+{s}}\right]_{{x}} ^{\mathrm{1}} +\int_{{x}} ^{\mathrm{1}} \frac{\mathrm{1}}{{s}\left({s}+\mathrm{1}\right)}{ds}\right] \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{k}} \frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)^{\mathrm{2}} }−\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\frac{{ln}\left({x}\right)}{\mathrm{1}+{x}}+\int_{{x}} ^{\mathrm{1}} \frac{\mathrm{1}}{{s}}{ds}−\int_{{x}} ^{\mathrm{1}} \frac{\mathrm{1}}{{s}+\mathrm{1}}{dx}\right\} \\ $$$${I}=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\frac{{ln}\left({x}\right)}{\mathrm{1}+{x}}−{ln}\left({x}\right)−{ln}\left(\mathrm{2}\right)+{ln}\left({x}+\mathrm{1}\right)\right\}=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}+{ln}\left(\mathrm{2}\right) \\ $$$${J}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left({s}\right)}{\left(\mathrm{1}+{s}\right)^{\mathrm{4}} }{ds} \\ $$$$\left.=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[−\frac{{ln}^{\mathrm{2}} \left({s}\right)}{\mathrm{3}\left(\mathrm{1}+{s}\right)^{\mathrm{3}} }\right]_{{x}} ^{\mathrm{1}} +\frac{\mathrm{2}}{\mathrm{3}}\int_{{x}} ^{\mathrm{1}} \frac{{ln}\left({s}\right)}{{s}\left(\mathrm{1}+{s}\right)^{\mathrm{3}} }{ds}\right] \\ $$$$\frac{\mathrm{1}}{{s}\left(\mathrm{1}+{s}\right)^{\mathrm{3}} }=\frac{\left(\mathrm{1}+{s}\right)^{\mathrm{3}} −{s}\left(\mathrm{1}+{s}\right)^{\mathrm{2}} −{s}\left(\mathrm{1}+{s}\right)−{s}}{{s}\left(\mathrm{1}+{s}\right)^{\mathrm{3}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{ln}^{\mathrm{2}} \left({x}\right)}{\mathrm{3}\left(\mathrm{1}+{x}\right)^{\mathrm{3}} }+\frac{\mathrm{2}}{\mathrm{3}}\int_{{x}} ^{\mathrm{1}} \left(\frac{{ln}\left({s}\right)}{{s}}−\frac{{ln}\left({s}\right)}{\mathrm{1}+{s}}−\frac{{ln}\left({s}\right)}{\left(\mathrm{1}+{s}\right)^{\mathrm{2}} }−\frac{{ln}\left({s}\right)}{\left(\mathrm{1}+{s}\right)^{\mathrm{3}} }\right) \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{{ln}^{\mathrm{2}} \left({x}\right)}{\mathrm{3}\left(\mathrm{1}+{x}\right)^{\mathrm{3}} }−\frac{{ln}^{\mathrm{2}} \left({x}\right)}{\mathrm{3}}\right)_{=\mathrm{0}} −\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({s}\right)}{\mathrm{1}+{s}}{ds}−\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({s}\right)}{\left(\mathrm{1}+{s}\right)^{\mathrm{2}} }−\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=−\frac{\mathrm{2}}{\mathrm{3}}\Sigma\frac{\left(−\mathrm{1}\right)^{{k}} }{\left({k}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{2}}{\mathrm{3}}.−{ln}\left(\mathrm{2}\right)−\frac{\mathrm{2}}{\mathrm{3}}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\left[\frac{−{ln}\left({s}\right)}{\mathrm{2}\left(\mathrm{1}+{s}\right)^{\mathrm{2}} }\right]_{{x}} ^{\mathrm{1}} +\int_{{x}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}{s}\left(\mathrm{1}+{s}\right)^{\mathrm{2}} }\right\} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{18}}+\frac{\mathrm{2}{ln}\left(\mathrm{2}\right)}{\mathrm{3}}−\frac{\mathrm{2}}{\mathrm{3}}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\frac{{ln}\left({x}\right)}{\mathrm{2}\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }+\int_{{x}} ^{\mathrm{1}} \frac{\left(\mathrm{1}+{s}\right)^{\mathrm{2}} −{s}\left(\mathrm{1}+{s}\right)−{s}}{\mathrm{2}{s}\left({s}+\mathrm{1}\right)^{\mathrm{2}} }{ds}\right. \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{18}}+\frac{\mathrm{2}{ln}\left(\mathrm{2}\right)}{\mathrm{3}}−\frac{\mathrm{2}}{\mathrm{3}}\left[\frac{{ln}\left({x}\right)}{\mathrm{2}\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }+\int_{{x}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}{s}}{ds}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{s}}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\left(\mathrm{1}+{s}\right)^{\mathrm{2}} }\right] \\ $$$$\left.=\frac{\pi^{\mathrm{2}} }{\mathrm{18}}+\frac{\mathrm{2}{ln}\left(\mathrm{2}\right)}{\mathrm{3}}−\frac{\mathrm{2}}{\mathrm{3}}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\left[\frac{{ln}\left({x}\right)}{\mathrm{2}\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }−\frac{{ln}\left({x}\right)}{\mathrm{2}}\right]_{} −\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)\right]\right\} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{18}}+\frac{\mathrm{2}{ln}\left(\mathrm{2}\right)}{\mathrm{3}}+\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{16}}=\frac{\pi^{\mathrm{2}} }{\mathrm{18}}+{ln}\left(\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\Psi=\frac{\mathrm{2}}{{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}\left[{I}−{J}\right]=\frac{\mathrm{2}}{{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}\left[\frac{\pi^{\mathrm{2}} }{\mathrm{12}}+{ln}\left(\mathrm{2}\right)−\left(\frac{\pi^{\mathrm{2}} }{\mathrm{18}}+{ln}\left(\mathrm{2}\right)+\frac{\mathrm{1}}{\mathrm{6}}\right)\right] \\ $$$$=\frac{\mathrm{2}}{{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}\left[\frac{\pi^{\mathrm{2}} −\mathrm{6}}{\mathrm{36}}\right]=\frac{\pi^{\mathrm{2}} −\mathrm{6}}{\mathrm{18}{ln}^{\mathrm{3}} \left(\mathrm{2}\right)} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
