Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 115951 by Fikret last updated on 29/Sep/20

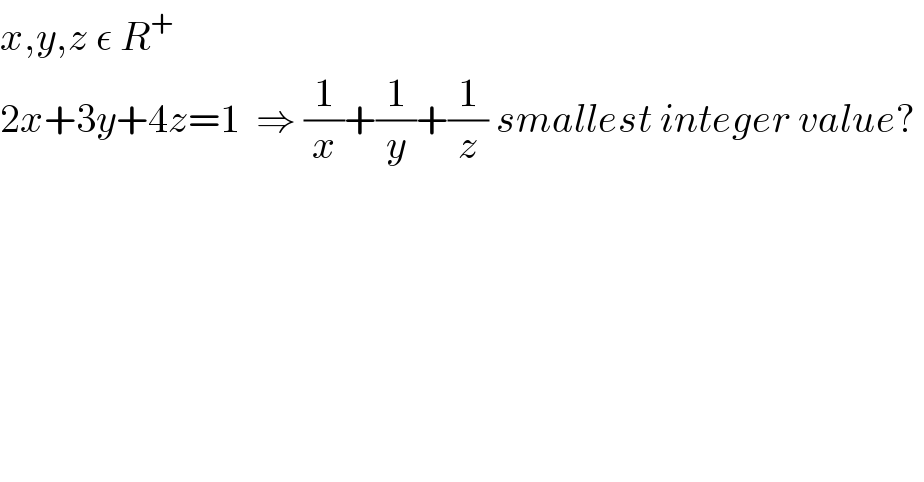
x,y,z ε R^+ 2x+3y+4z=1 ⇒ (1/x)+(1/y)+(1/z) smallest integer value?

$${x},{y},{z}\:\epsilon\:{R}^{+} \:\: \\ $$$$\mathrm{2}{x}+\mathrm{3}{y}+\mathrm{4}{z}=\mathrm{1}\:\:\Rightarrow\:\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}\:{smallest}\:{integer}\:{value}?\: \\ $$

Answered by 1549442205PVT last updated on 30/Sep/20

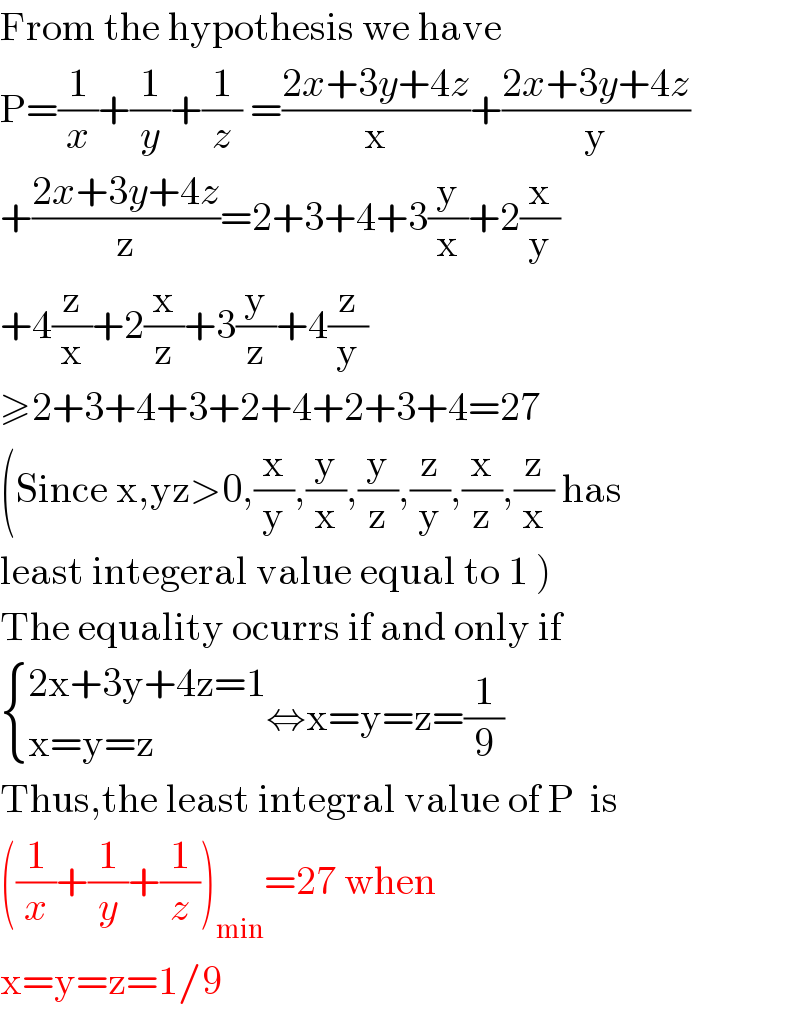
From the hypothesis we have P=(1/x)+(1/y)+(1/z) =((2x+3y+4z)/x)+((2x+3y+4z)/y) +((2x+3y+4z)/z)=2+3+4+3(y/x)+2(x/y) +4(z/x)+2(x/z)+3(y/z)+4(z/y) ≥2+3+4+3+2+4+2+3+4=27 (Since x,yz>0,(x/y),(y/x),(y/z),(z/y),(x/z),(z/x) has least integeral value equal to 1 ) The equality ocurrs if and only if { ((2x+3y+4z=1)),((x=y=z)) :}⇔x=y=z=(1/9) Thus,the least integral value of P is ((1/x)+(1/y)+(1/z))_(min) =27 when x=y=z=1/9

$$\mathrm{From}\:\mathrm{the}\:\mathrm{hypothesis}\:\mathrm{we}\:\mathrm{have}\: \\ $$$$\mathrm{P}=\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}\:=\frac{\mathrm{2}{x}+\mathrm{3}{y}+\mathrm{4}{z}}{\mathrm{x}}+\frac{\mathrm{2}{x}+\mathrm{3}{y}+\mathrm{4}{z}}{\mathrm{y}} \\ $$$$+\frac{\mathrm{2}{x}+\mathrm{3}{y}+\mathrm{4}{z}}{\mathrm{z}}=\mathrm{2}+\mathrm{3}+\mathrm{4}+\mathrm{3}\frac{\mathrm{y}}{\mathrm{x}}+\mathrm{2}\frac{\mathrm{x}}{\mathrm{y}} \\ $$$$+\mathrm{4}\frac{\mathrm{z}}{\mathrm{x}}+\mathrm{2}\frac{\mathrm{x}}{\mathrm{z}}+\mathrm{3}\frac{\mathrm{y}}{\mathrm{z}}+\mathrm{4}\frac{\mathrm{z}}{\mathrm{y}} \\ $$$$\geqslant\mathrm{2}+\mathrm{3}+\mathrm{4}+\mathrm{3}+\mathrm{2}+\mathrm{4}+\mathrm{2}+\mathrm{3}+\mathrm{4}=\mathrm{27} \\ $$$$\left(\mathrm{Since}\:\mathrm{x},\mathrm{yz}>\mathrm{0},\frac{\mathrm{x}}{\mathrm{y}},\frac{\mathrm{y}}{\mathrm{x}},\frac{\mathrm{y}}{\mathrm{z}},\frac{\mathrm{z}}{\mathrm{y}},\frac{\mathrm{x}}{\mathrm{z}},\frac{\mathrm{z}}{\mathrm{x}}\:\mathrm{has}\right. \\ $$$$\left.\mathrm{least}\:\mathrm{integeral}\:\mathrm{value}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{1}\:\right) \\ $$$$\mathrm{The}\:\mathrm{equality}\:\mathrm{ocurrs}\:\mathrm{if}\:\mathrm{and}\:\mathrm{only}\:\mathrm{if} \\ $$$$\begin{cases}{\mathrm{2x}+\mathrm{3y}+\mathrm{4z}=\mathrm{1}}\\{\mathrm{x}=\mathrm{y}=\mathrm{z}}\end{cases}\Leftrightarrow\mathrm{x}=\mathrm{y}=\mathrm{z}=\frac{\mathrm{1}}{\mathrm{9}} \\ $$$$\mathrm{Thus},\mathrm{the}\:\mathrm{least}\:\mathrm{integral}\:\mathrm{value}\:\mathrm{of}\:\mathrm{P}\:\:\mathrm{is} \\ $$$$\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}\right)_{\mathrm{min}} =\mathrm{27}\:\mathrm{when} \\ $$$$\mathrm{x}=\mathrm{y}=\mathrm{z}=\mathrm{1}/\mathrm{9} \\ $$

Commented by soumyasaha last updated on 01/Oct/20

Assuming x, y, z positive, we have ((2x+3y+4z)/3) ≥ ((2x.3y.4z))^(1/3) ⇒ 24xyz ≤ (1/(27)) ⇒ (1/(xyz)) ≥ 27.24 ..........(i) Again, (((1/x)+(1/y)+(1/z))/3) ≥ (((1/x).(1/y).(1/y)))^(1/3) ⇒ (1/x)+(1/y)+(1/z) ≥ 3.((1/(xyz)))^(1/3) ⇒ (1/x)+(1/y)+(1/z) ≥ 3.((27.24))^(1/3) ⇒ (1/x)+(1/y)+(1/z) ≥ 18.(3)^(1/3) ∴ least integral value is 26

$$\: \\ $$$$\:\:\mathrm{Assuming}\:\mathrm{x},\:\mathrm{y},\:\mathrm{z}\:\mathrm{positive},\:\mathrm{we}\:\mathrm{have} \\ $$$$\:\:\:\:\frac{\mathrm{2x}+\mathrm{3y}+\mathrm{4z}}{\mathrm{3}}\:\geqslant\:\sqrt[{\mathrm{3}}]{\mathrm{2x}.\mathrm{3y}.\mathrm{4z}} \\ $$$$\:\:\:\:\Rightarrow\:\mathrm{24xyz}\:\leqslant\:\frac{\mathrm{1}}{\mathrm{27}} \\ $$$$\:\:\:\:\Rightarrow\:\frac{\mathrm{1}}{\mathrm{xyz}}\:\geqslant\:\mathrm{27}.\mathrm{24}\:..........\left(\mathrm{i}\right) \\ $$$$ \\ $$$$\:\:\mathrm{Again},\:\:\frac{\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{y}}+\frac{\mathrm{1}}{\mathrm{z}}}{\mathrm{3}}\:\geqslant\:\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}}{\mathrm{x}}.\frac{\mathrm{1}}{\mathrm{y}}.\frac{\mathrm{1}}{\mathrm{y}}} \\ $$$$\:\:\Rightarrow\:\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{y}}+\frac{\mathrm{1}}{\mathrm{z}}\:\geqslant\:\mathrm{3}.\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}}{\mathrm{xyz}}} \\ $$$$\:\:\Rightarrow\:\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{y}}+\frac{\mathrm{1}}{\mathrm{z}}\:\geqslant\:\mathrm{3}.\sqrt[{\mathrm{3}}]{\mathrm{27}.\mathrm{24}} \\ $$$$\:\:\Rightarrow\:\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{y}}+\frac{\mathrm{1}}{\mathrm{z}}\:\geqslant\:\mathrm{18}.\sqrt[{\mathrm{3}}]{\mathrm{3}} \\ $$$$\:\therefore\:\mathrm{least}\:\mathrm{integral}\:\mathrm{value}\:\mathrm{is}\:\mathrm{26} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com