
Question Number 116014 by mnjuly1970 last updated on 30/Sep/20
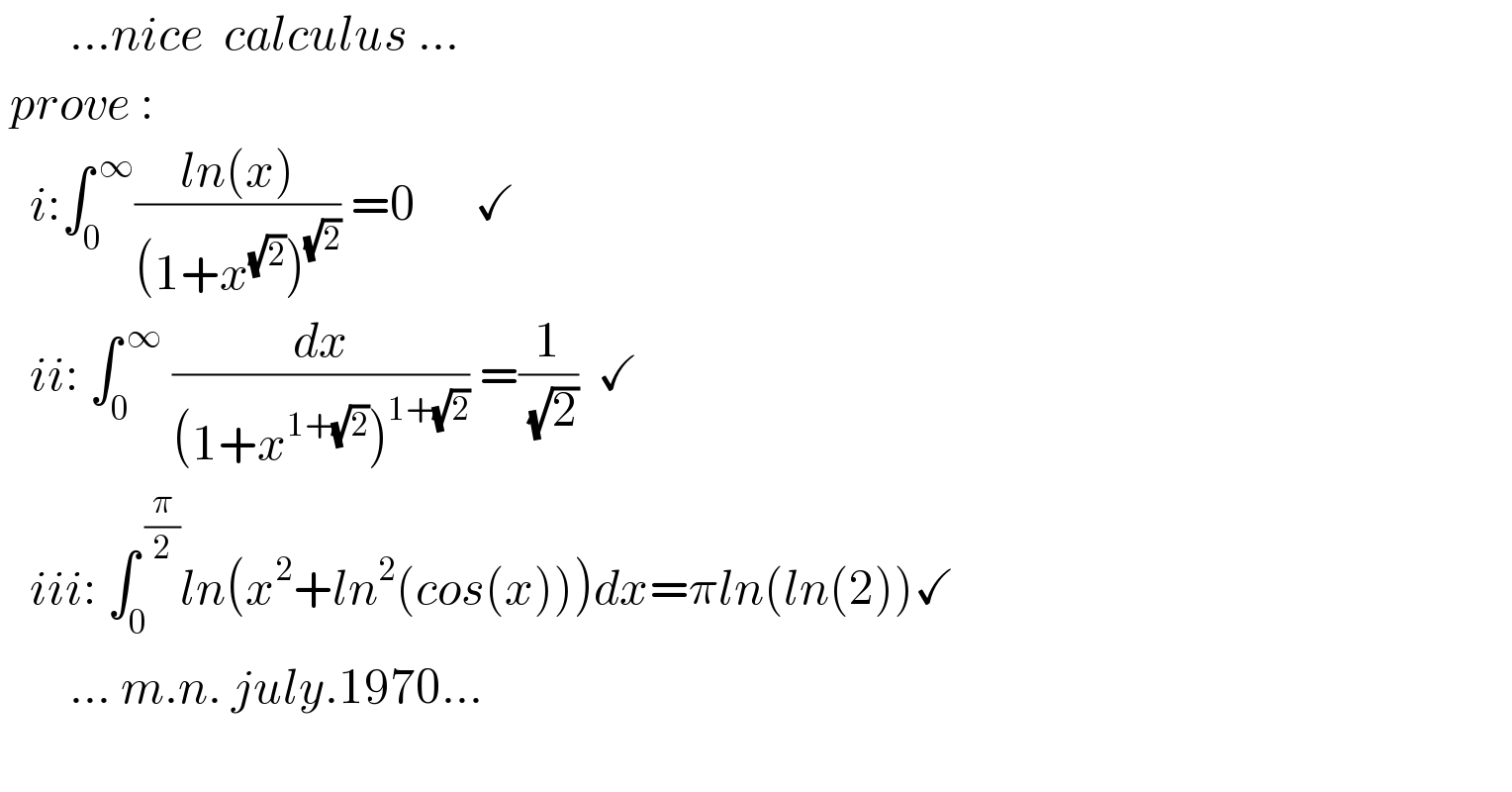
$$\:\:\:\:\:\:\:...{nice}\:\:{calculus}\:...\:\:\: \\ $$$$\:{prove}\:: \\ $$$$\:\:\:{i}:\int_{\mathrm{0}} ^{\:\infty} \frac{{ln}\left({x}\right)}{\left(\mathrm{1}+{x}^{\sqrt{\mathrm{2}}} \right)^{\sqrt{\mathrm{2}}} }\:=\mathrm{0}\:\:\:\:\:\:\checkmark \\ $$$$\:\:\:{ii}:\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{1}+\sqrt{\mathrm{2}}} \right)^{\mathrm{1}+\sqrt{\mathrm{2}}} }\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\:\checkmark\:\: \\ $$$$\:\:\:{iii}:\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {ln}\left({x}^{\mathrm{2}} +{ln}^{\mathrm{2}} \left({cos}\left({x}\right)\right)\right){dx}=\pi{ln}\left({ln}\left(\mathrm{2}\right)\right)\checkmark \\ $$$$\:\:\:\:\:\:\:...\:{m}.{n}.\:{july}.\mathrm{1970}... \\ $$$$ \\ $$
Answered by mindispower last updated on 30/Sep/20
![i) t=(1/x)⇒ i=∫^0 _∞ ((ln(t)dt)/(t^2 (((1+t^(√2) )/t^(√2) ))^(√2) ))=−∫_0 ^∞ ((ln(t)dt)/((1+t^(√2) )^(√2) )) i=−i⇒i=0 ii)t=(1/x) =∫_0 ^∞ ((t^(1+2(√2)) dt)/((t^(1+(√2)) +1)^(1+(√2)) )) ∫_0 ^∞ ((t^(1+2(√2)) +t^(√2) )/((t^(1+(√2)) +1)^(1+(√2)) ))dt−∫_0 ^∞ (t^(√2) /((t^(1+(√2)) +1)^(1+(√2)) ))dt I−J I=∫_0 ^∞ (t^(√2) /((t^(1+(√2)) +1)^(√2) ))dt t^(1+(√2)) =y⇒dy=(1+(√2))t^(√2) =∫_0 ^∞ (dy/((1+(√2))(y+1)^(√2) ))=∫_0 ^∞ (1/((1+(√2))))(y+1)^(−(√2)) =[−(y+1)^(1−(√2)) ]_0 ^∞ =1 J,y=t^(1+(√2)) dt=(dy/(1+(√2))) =∫_0 ^∞ (dy/((1+(√2))(y+1)^(1+(√2)) )) =∫_0 ^∞ (1/(((√2)+1)))(y+1)^(−1−(√2)) dy =[_0 ^∞ (((y+1)^(−1−(√2)) )/((1+(√2))(−(√2))))]=(1/( (√2)(1+(√2))))=(1/( (√2)))((√2)−1) I−J=1−(1/( (√2)))((√2)−1)=(1/( (√2))) iii) not nice ideas](Q116046.png)
$$\left.{i}\right)\:{t}=\frac{\mathrm{1}}{{x}}\Rightarrow \\ $$$${i}=\underset{\infty} {\int}^{\mathrm{0}} \frac{{ln}\left({t}\right){dt}}{{t}^{\mathrm{2}} \left(\frac{\mathrm{1}+{t}^{\sqrt{\mathrm{2}}} }{{t}^{\sqrt{\mathrm{2}}} }\right)^{\sqrt{\mathrm{2}}} }=−\int_{\mathrm{0}} ^{\infty} \frac{{ln}\left({t}\right){dt}}{\left(\mathrm{1}+{t}^{\sqrt{\mathrm{2}}} \right)^{\sqrt{\mathrm{2}}} }\: \\ $$$${i}=−{i}\Rightarrow{i}=\mathrm{0} \\ $$$$\left.{ii}\right){t}=\frac{\mathrm{1}}{{x}} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}} {dt}}{\left({t}^{\mathrm{1}+\sqrt{\mathrm{2}}} +\mathrm{1}\right)^{\mathrm{1}+\sqrt{\mathrm{2}}} } \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}} +{t}^{\sqrt{\mathrm{2}}} }{\left({t}^{\mathrm{1}+\sqrt{\mathrm{2}}} +\mathrm{1}\right)^{\mathrm{1}+\sqrt{\mathrm{2}}} }{dt}−\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\sqrt{\mathrm{2}}} }{\left({t}^{\mathrm{1}+\sqrt{\mathrm{2}}} +\mathrm{1}\right)^{\mathrm{1}+\sqrt{\mathrm{2}}} }{dt} \\ $$$${I}−{J} \\ $$$${I}=\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\sqrt{\mathrm{2}}} }{\left({t}^{\mathrm{1}+\sqrt{\mathrm{2}}} +\mathrm{1}\right)^{\sqrt{\mathrm{2}}} }{dt} \\ $$$${t}^{\mathrm{1}+\sqrt{\mathrm{2}}} ={y}\Rightarrow{dy}=\left(\mathrm{1}+\sqrt{\mathrm{2}}\right){t}^{\sqrt{\mathrm{2}}} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{dy}}{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\left({y}+\mathrm{1}\right)^{\sqrt{\mathrm{2}}} }=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}\left({y}+\mathrm{1}\right)^{−\sqrt{\mathrm{2}}} \\ $$$$=\left[−\left({y}+\mathrm{1}\right)^{\mathrm{1}−\sqrt{\mathrm{2}}} \right]_{\mathrm{0}} ^{\infty} =\mathrm{1} \\ $$$${J},{y}={t}^{\mathrm{1}+\sqrt{\mathrm{2}}} \\ $$$${dt}=\frac{{dy}}{\mathrm{1}+\sqrt{\mathrm{2}}} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{dy}}{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\left({y}+\mathrm{1}\right)^{\mathrm{1}+\sqrt{\mathrm{2}}} } \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)}\left({y}+\mathrm{1}\right)^{−\mathrm{1}−\sqrt{\mathrm{2}}} {dy} \\ $$$$=\left[_{\mathrm{0}} ^{\infty} \frac{\left({y}+\mathrm{1}\right)^{−\mathrm{1}−\sqrt{\mathrm{2}}} }{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\left(−\sqrt{\mathrm{2}}\right)}\right]=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right) \\ $$$${I}−{J}=\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\left.{iii}\right)\:{not}\:{nice}\:{ideas} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 30/Sep/20
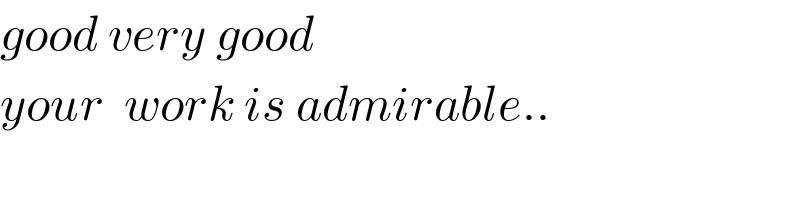
$${good}\:{very}\:{good} \\ $$$${your}\:\:{work}\:{is}\:{admirable}.. \\ $$
Commented by mindispower last updated on 30/Sep/20
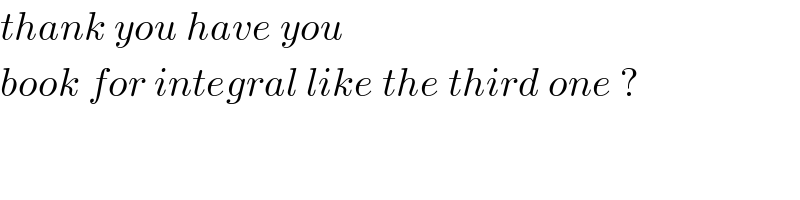
$${thank}\:{you}\:{have}\:{you}\: \\ $$$${book}\:{for}\:{integral}\:{like}\:{the}\:{third}\:{one}\:? \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 30/Sep/20
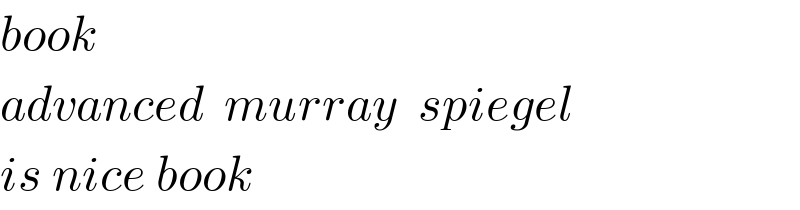
$${book} \\ $$$${advanced}\:\:{murray}\:\:{spiegel} \\ $$$${is}\:{nice}\:{book}\: \\ $$
Commented by mindispower last updated on 01/Oct/20
$${thank}\:{you} \\ $$$$\left.{have}\:{you}\:{solution}\:{for}\:{the}\:{iii}\right){please}\:{sir} \\ $$
