Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 117638 by bemath last updated on 13/Oct/20

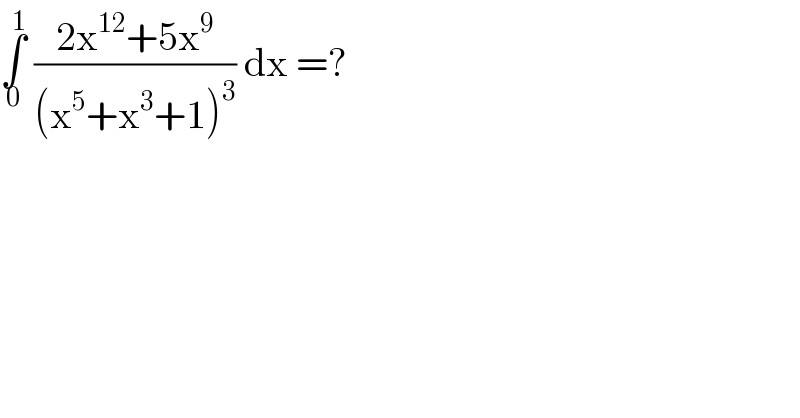
∫_0 ^1 ((2x^(12) +5x^9 )/((x^5 +x^3 +1)^3 )) dx =?

$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{\mathrm{2x}^{\mathrm{12}} +\mathrm{5x}^{\mathrm{9}} }{\left(\mathrm{x}^{\mathrm{5}} +\mathrm{x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{3}} }\:\mathrm{dx}\:=?\: \\ $$

Answered by john santu last updated on 13/Oct/20

I=∫_0 ^1 ((2x^(12) +5x^9 )/((x^5 (1+x^(−2) +x^(−5) ))^3 )) dx I=∫_0 ^1 ((2x^(12) +5x^9 )/(x^(15) (1+x^(−2) +x^(−5) )^3 )) dx I= ∫_0 ^1 ((2x^(−3) +5x^(−6) )/((1+x^(−2) +x^(−5) )^3 )) dx Letting ψ=1+x^(−2) +x^(−5) →dψ=−2x^(−3) −5x^(−6) dx I=lim_(b→∞) ∫_b ^3 ((−dψ)/ψ^3 ) = −lim_(b→∞) ∫_b ^3 ψ^(−3) dψ I=(1/2).lim_(b→∞) [ (1/ψ^2 ) ]_b ^3 = (1/2)[ (1/9) −0 ] = (1/(18))

$${I}=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{\mathrm{2}{x}^{\mathrm{12}} +\mathrm{5}{x}^{\mathrm{9}} }{\left({x}^{\mathrm{5}} \left(\mathrm{1}+{x}^{−\mathrm{2}} +{x}^{−\mathrm{5}} \right)\right)^{\mathrm{3}} }\:{dx}\: \\ $$$${I}=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{\mathrm{2}{x}^{\mathrm{12}} +\mathrm{5}{x}^{\mathrm{9}} }{{x}^{\mathrm{15}} \left(\mathrm{1}+{x}^{−\mathrm{2}} +{x}^{−\mathrm{5}} \right)^{\mathrm{3}} }\:{dx} \\ $$$${I}=\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{\mathrm{2}{x}^{−\mathrm{3}} +\mathrm{5}{x}^{−\mathrm{6}} }{\left(\mathrm{1}+{x}^{−\mathrm{2}} +{x}^{−\mathrm{5}} \right)^{\mathrm{3}} }\:{dx} \\ $$$${Letting}\:\psi=\mathrm{1}+{x}^{−\mathrm{2}} +{x}^{−\mathrm{5}} \:\rightarrow{d}\psi=−\mathrm{2}{x}^{−\mathrm{3}} −\mathrm{5}{x}^{−\mathrm{6}} \:{dx} \\ $$$${I}=\underset{{b}\rightarrow\infty} {\mathrm{lim}}\:\underset{{b}} {\overset{\mathrm{3}} {\int}}\:\frac{−{d}\psi}{\psi^{\mathrm{3}} }\:=\:−\underset{{b}\rightarrow\infty} {\mathrm{lim}}\:\underset{{b}} {\overset{\mathrm{3}} {\int}}\:\psi^{−\mathrm{3}} \:{d}\psi \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}.\underset{{b}\rightarrow\infty} {\mathrm{lim}}\:\left[\:\frac{\mathrm{1}}{\psi^{\mathrm{2}} }\:\right]_{{b}} ^{\mathrm{3}} =\:\frac{\mathrm{1}}{\mathrm{2}}\left[\:\frac{\mathrm{1}}{\mathrm{9}}\:−\mathrm{0}\:\right]\:=\:\frac{\mathrm{1}}{\mathrm{18}} \\ $$

Commented by bemath last updated on 13/Oct/20

gave kudos

$$\mathrm{gave}\:\mathrm{kudos} \\ $$

Answered by 1549442205PVT last updated on 13/Oct/20

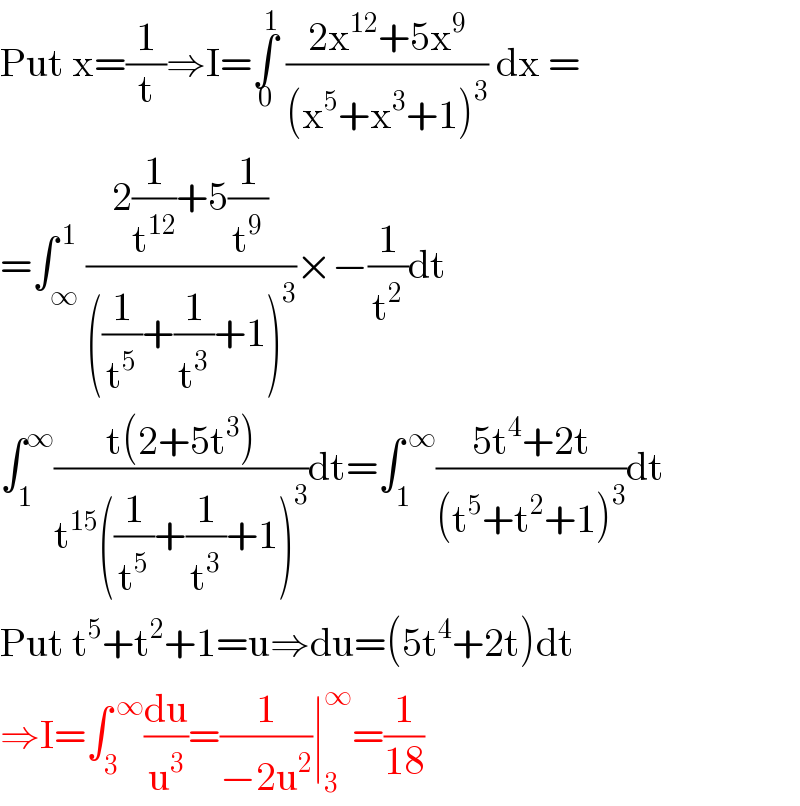
Put x=(1/t)⇒I=∫_0 ^1 ((2x^(12) +5x^9 )/((x^5 +x^3 +1)^3 )) dx = =∫_∞ ^( 1) ((2(1/t^(12) )+5(1/t^9 ))/(((1/t^5 )+(1/t^3 )+1)^3 ))×−(1/t^2 )dt ∫_1 ^∞ ((t(2+5t^3 ))/(t^(15) ((1/t^5 )+(1/t^3 )+1)^3 ))dt=∫_1 ^( ∞) ((5t^4 +2t)/((t^5 +t^2 +1)^3 ))dt Put t^5 +t^2 +1=u⇒du=(5t^4 +2t)dt ⇒I=∫_3 ^( ∞) (du/u^3 )=(1/(−2u^2 ))∣_3 ^∞ =(1/(18))

$$\mathrm{Put}\:\mathrm{x}=\frac{\mathrm{1}}{\mathrm{t}}\Rightarrow\mathrm{I}=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{\mathrm{2x}^{\mathrm{12}} +\mathrm{5x}^{\mathrm{9}} }{\left(\mathrm{x}^{\mathrm{5}} +\mathrm{x}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{3}} }\:\mathrm{dx}\:= \\ $$$$=\int_{\infty} ^{\:\mathrm{1}} \frac{\mathrm{2}\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{12}} }+\mathrm{5}\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{9}} }}{\left(\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{5}} }+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{3}} }+\mathrm{1}\right)^{\mathrm{3}} }×−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{t}\left(\mathrm{2}+\mathrm{5t}^{\mathrm{3}} \right)}{\mathrm{t}^{\mathrm{15}} \left(\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{5}} }+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{3}} }+\mathrm{1}\right)^{\mathrm{3}} }\mathrm{dt}=\int_{\mathrm{1}} ^{\:\infty} \frac{\mathrm{5t}^{\mathrm{4}} +\mathrm{2t}}{\left(\mathrm{t}^{\mathrm{5}} +\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }\mathrm{dt} \\ $$$$\mathrm{Put}\:\mathrm{t}^{\mathrm{5}} +\mathrm{t}^{\mathrm{2}} +\mathrm{1}=\mathrm{u}\Rightarrow\mathrm{du}=\left(\mathrm{5t}^{\mathrm{4}} +\mathrm{2t}\right)\mathrm{dt} \\ $$$$\Rightarrow\mathrm{I}=\int_{\mathrm{3}} ^{\:\infty} \frac{\mathrm{du}}{\mathrm{u}^{\mathrm{3}} }=\frac{\mathrm{1}}{−\mathrm{2u}^{\mathrm{2}} }\mid_{\mathrm{3}} ^{\infty} =\frac{\mathrm{1}}{\mathrm{18}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com