Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 118924 by mnjuly1970 last updated on 21/Oct/20

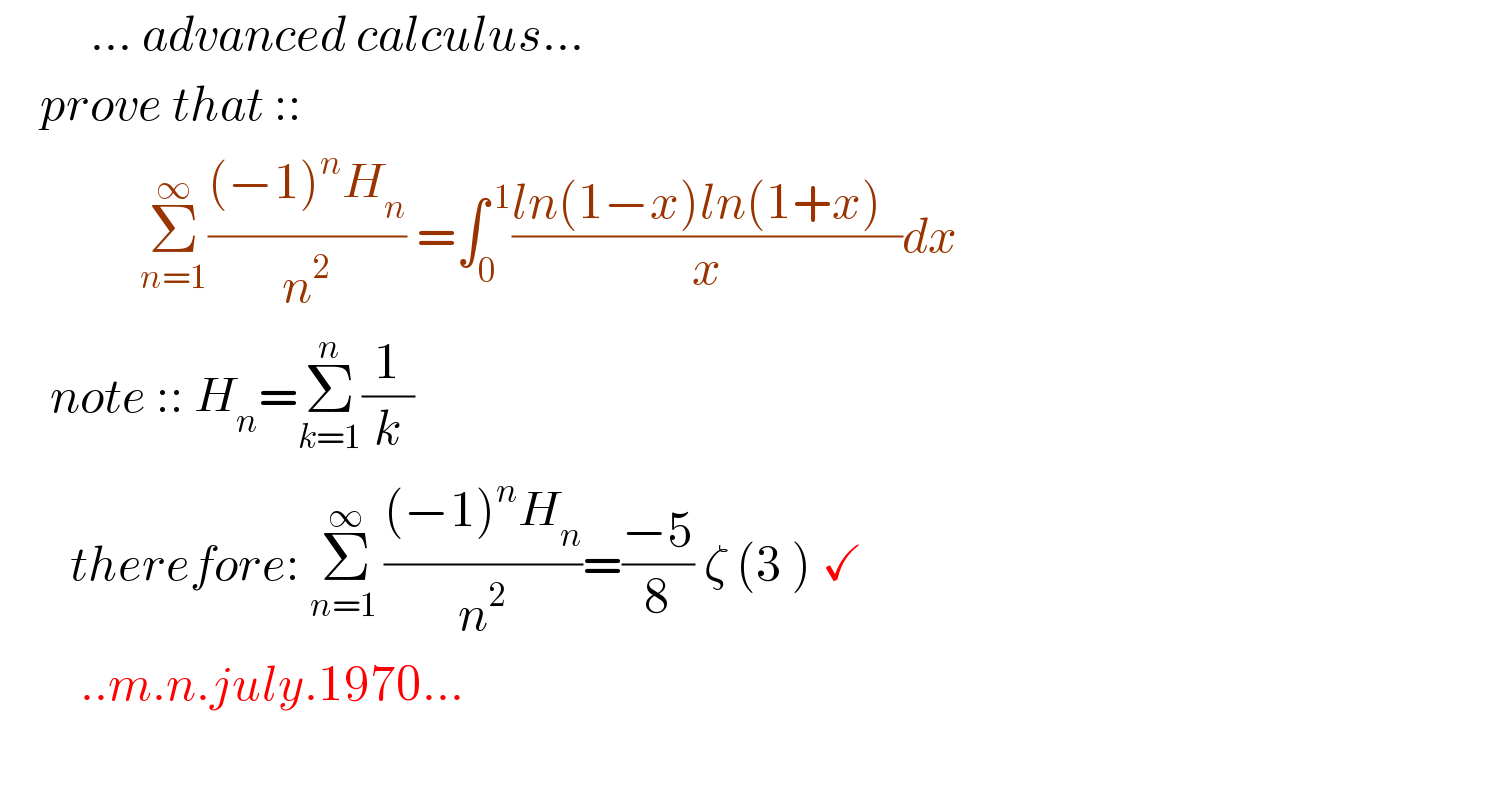
... advanced calculus... prove that :: Σ_(n=1) ^∞ (((−1)^n H_n )/n^2 ) =∫_0 ^( 1) ((ln(1−x)ln(1+x) )/x)dx note :: H_n =Σ_(k=1) ^n (1/k) therefore: Σ_(n=1 ) ^∞ (((−1)^n H_n )/n^2 )=((−5)/8) ζ (3 ) ✓ ..m.n.july.1970...

$$\:\:\:\:\:\:\:\:\:...\:{advanced}\:{calculus}... \\ $$$$\:\:\:\:{prove}\:{that}\::: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {H}_{{n}} }{{n}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}\right){ln}\left(\mathrm{1}+{x}\right)\:\:}{{x}}{dx}\:\: \\ $$$$\:\:\:\:\:{note}\:::\:{H}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}} \\ $$$$\:\:\:\:\:\:\:{therefore}:\:\underset{{n}=\mathrm{1}\:} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {H}_{{n}} }{{n}^{\mathrm{2}} }=\frac{−\mathrm{5}}{\mathrm{8}}\:\zeta\:\left(\mathrm{3}\:\right)\:\checkmark \\ $$$$\:\:\:\:\:\:\:\:..{m}.{n}.{july}.\mathrm{1970}... \\ $$$$ \\ $$

Answered by mindispower last updated on 21/Oct/20

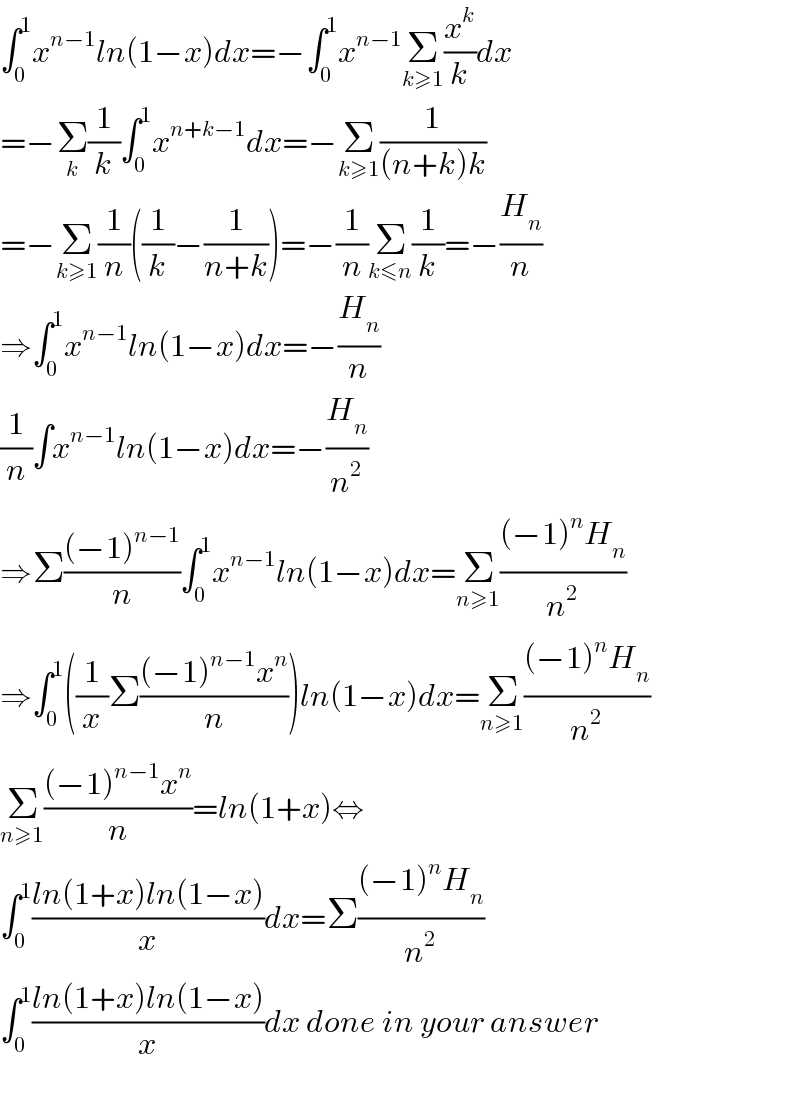
∫_0 ^1 x^(n−1) ln(1−x)dx=−∫_0 ^1 x^(n−1) Σ_(k≥1) (x^k /k)dx =−Σ_k (1/k)∫_0 ^1 x^(n+k−1) dx=−Σ_(k≥1) (1/((n+k)k)) =−Σ_(k≥1) (1/n)((1/k)−(1/(n+k)))=−(1/n)Σ_(k≤n) (1/k)=−(H_n /n) ⇒∫_0 ^1 x^(n−1) ln(1−x)dx=−(H_n /n) (1/n)∫x^(n−1) ln(1−x)dx=−(H_n /n^2 ) ⇒Σ(((−1)^(n−1) )/n)∫_0 ^1 x^(n−1) ln(1−x)dx=Σ_(n≥1) (((−1)^n H_n )/n^2 ) ⇒∫_0 ^1 ((1/x)Σ(((−1)^(n−1) x^n )/n))ln(1−x)dx=Σ_(n≥1) (((−1)^n H_n )/n^2 ) Σ_(n≥1) (((−1)^(n−1) x^n )/n)=ln(1+x)⇔ ∫_0 ^1 ((ln(1+x)ln(1−x))/x)dx=Σ(((−1)^n H_n )/n^2 ) ∫_0 ^1 ((ln(1+x)ln(1−x))/x)dx done in your answer

$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}−\mathrm{1}} {ln}\left(\mathrm{1}−{x}\right){dx}=−\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}−\mathrm{1}} \underset{{k}\geqslant\mathrm{1}} {\sum}\frac{{x}^{{k}} }{{k}}{dx} \\ $$$$=−\underset{{k}} {\sum}\frac{\mathrm{1}}{{k}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}+{k}−\mathrm{1}} {dx}=−\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left({n}+{k}\right){k}} \\ $$$$=−\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}}\left(\frac{\mathrm{1}}{{k}}−\frac{\mathrm{1}}{{n}+{k}}\right)=−\frac{\mathrm{1}}{{n}}\underset{{k}\leqslant{n}} {\sum}\frac{\mathrm{1}}{{k}}=−\frac{{H}_{{n}} }{{n}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}−\mathrm{1}} {ln}\left(\mathrm{1}−{x}\right){dx}=−\frac{{H}_{{n}} }{{n}} \\ $$$$\frac{\mathrm{1}}{{n}}\int{x}^{{n}−\mathrm{1}} {ln}\left(\mathrm{1}−{x}\right){dx}=−\frac{{H}_{{n}} }{{n}^{\mathrm{2}} } \\ $$$$\Rightarrow\Sigma\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}−\mathrm{1}} {ln}\left(\mathrm{1}−{x}\right){dx}=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} {H}_{{n}} }{{n}^{\mathrm{2}} } \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}}{{x}}\Sigma\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {x}^{{n}} }{{n}}\right){ln}\left(\mathrm{1}−{x}\right){dx}=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} {H}_{{n}} }{{n}^{\mathrm{2}} } \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {x}^{{n}} }{{n}}={ln}\left(\mathrm{1}+{x}\right)\Leftrightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}\right){ln}\left(\mathrm{1}−{x}\right)}{{x}}{dx}=\Sigma\frac{\left(−\mathrm{1}\right)^{{n}} {H}_{{n}} }{{n}^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}\right){ln}\left(\mathrm{1}−{x}\right)}{{x}}{dx}\:{done}\:{in}\:{your}\:{answer} \\ $$$$ \\ $$

Commented by mnjuly1970 last updated on 21/Oct/20

bravo bravo mr power grateful sir...

$${bravo}\:{bravo} \\ $$$${mr}\:{power}\: \\ $$$$\:{grateful}\:{sir}... \\ $$

Commented by mindispower last updated on 21/Oct/20

withe pleasur

$${withe}\:{pleasur} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com