Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 120091 by ZiYangLee last updated on 29/Oct/20

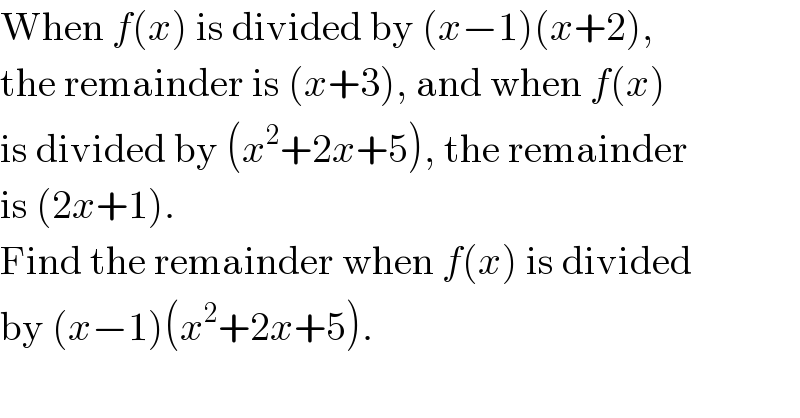
When f(x) is divided by (x−1)(x+2), the remainder is (x+3), and when f(x) is divided by (x^2 +2x+5), the remainder is (2x+1). Find the remainder when f(x) is divided by (x−1)(x^2 +2x+5).

$$\mathrm{When}\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{divided}\:\mathrm{by}\:\left({x}−\mathrm{1}\right)\left({x}+\mathrm{2}\right),\: \\ $$$$\mathrm{the}\:\mathrm{remainder}\:\mathrm{is}\:\left({x}+\mathrm{3}\right),\:\mathrm{and}\:\mathrm{when}\:{f}\left({x}\right) \\ $$$$\mathrm{is}\:\mathrm{divided}\:\mathrm{by}\:\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{5}\right),\:\mathrm{the}\:\mathrm{remainder} \\ $$$$\mathrm{is}\:\left(\mathrm{2}{x}+\mathrm{1}\right). \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{remainder}\:\mathrm{when}\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{divided} \\ $$$$\mathrm{by}\:\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{5}\right). \\ $$

Answered by TITA last updated on 29/Oct/20

for a given polynomial p(x)=f(x)q(x)+r where r is the remainder if r=o then q(x) divids p(x) let f(x)=p(x)(x−1)(x+2)+x+3.......(1) f(x)=p(x)(x^2 +2x+5)+2x+1........(2) (1)−(2)⇒ 0=p(x)[x^2 +x−2−(x^2 +2x+5)]+2−x ⇒x−2=p(x)[−x−7] ence p(x)=((2−x)/(x+7)) since f(x)=p(x)q(x)+r hence r=f(x)−p(x)q(x) (2)⇒f(x)=(((2−x)/(x+7)))(x^2 +2x+5)+2x+1 ⇒r=[(((2−x)/(x+7)))(x^2 +2x+5)+2x+1]−[(((2−x)/(x+7)))(x−1)(x^2 +2x+5)] ⇒r=(((2−x)/(x+7)))(x^2 +2x+5)[2−x] +2x+1 ⇒r=(((2−x)^2 (x^2 +2x+5))/(x+7))+2x+1

$$\mathrm{for}\:\mathrm{a}\:\mathrm{given}\:\mathrm{polynomial}\:\mathrm{p}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{x}\right)\mathrm{q}\left(\mathrm{x}\right)+{r} \\ $$$${where}\:{r}\:{is}\:{the}\:{remainder} \\ $$$$\mathrm{if}\:\mathrm{r}=\mathrm{o}\:\mathrm{then}\:\mathrm{q}\left(\mathrm{x}\right)\:\mathrm{divids}\:\mathrm{p}\left(\mathrm{x}\right) \\ $$$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{p}\left(\mathrm{x}\right)\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{2}\right)+\mathrm{x}+\mathrm{3}.......\left(\mathrm{1}\right) \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{p}\left(\mathrm{x}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{5}\right)+\mathrm{2}{x}+\mathrm{1}........\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)−\left(\mathrm{2}\right)\Rightarrow\:\mathrm{0}={p}\left({x}\right)\left[{x}^{\mathrm{2}} +{x}−\mathrm{2}−\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{5}\right)\right]+\mathrm{2}−{x} \\ $$$$\Rightarrow{x}−\mathrm{2}={p}\left({x}\right)\left[−{x}−\mathrm{7}\right] \\ $$$${ence}\:{p}\left({x}\right)=\frac{\mathrm{2}−{x}}{{x}+\mathrm{7}} \\ $$$${since}\:{f}\left({x}\right)={p}\left({x}\right){q}\left({x}\right)+{r}\: \\ $$$${hence}\:{r}={f}\left({x}\right)−{p}\left({x}\right){q}\left({x}\right) \\ $$$$\left(\mathrm{2}\right)\Rightarrow{f}\left({x}\right)=\left(\frac{\mathrm{2}−{x}}{{x}+\mathrm{7}}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{5}\right)+\mathrm{2}{x}+\mathrm{1} \\ $$$$\Rightarrow{r}=\left[\left(\frac{\mathrm{2}−{x}}{{x}+\mathrm{7}}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{5}\right)+\mathrm{2}{x}+\mathrm{1}\right]−\left[\left(\frac{\mathrm{2}−{x}}{{x}+\mathrm{7}}\right)\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{5}\right)\right] \\ $$$$\Rightarrow{r}=\left(\frac{\mathrm{2}−{x}}{{x}+\mathrm{7}}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{5}\right)\left[\mathrm{2}−{x}\right]\:+\mathrm{2}{x}+\mathrm{1} \\ $$$$\Rightarrow{r}=\frac{\left(\mathrm{2}−{x}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{5}\right)}{{x}+\mathrm{7}}+\mathrm{2}{x}+\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com