Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 120409 by SOMEDAVONG last updated on 31/Oct/20

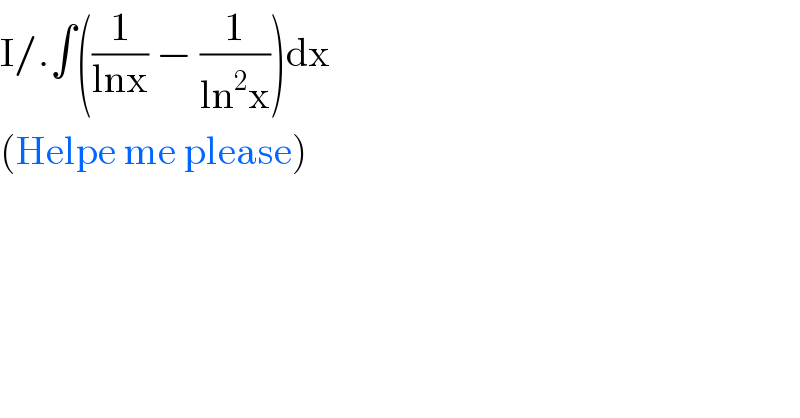
I/.∫((1/(lnx)) − (1/(ln^2 x)))dx (Helpe me please)

$$\mathrm{I}/.\int\left(\frac{\mathrm{1}}{\mathrm{lnx}}\:−\:\frac{\mathrm{1}}{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}\right)\mathrm{dx} \\ $$$$\left(\mathrm{Helpe}\:\mathrm{me}\:\mathrm{please}\right) \\ $$

Commented by soumyasaha last updated on 31/Oct/20

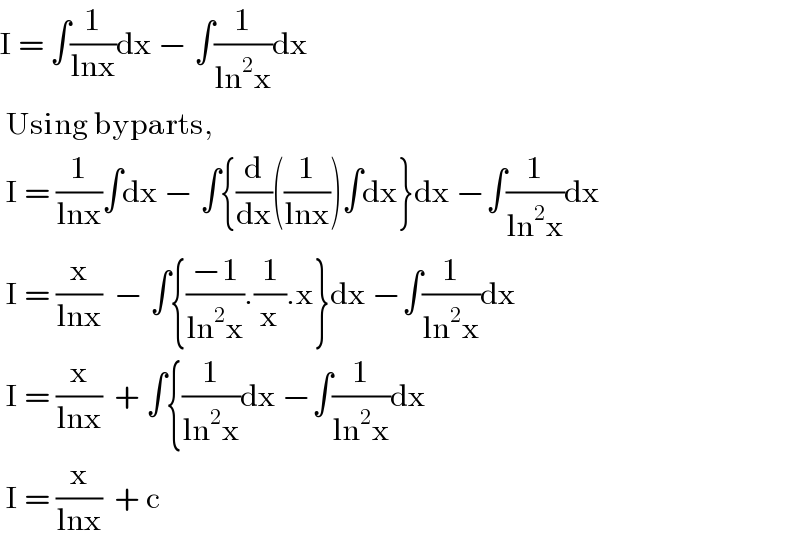
I = ∫(1/(lnx))dx − ∫(1/(ln^2 x))dx Using byparts, I = (1/(lnx))∫dx − ∫{(d/dx)((1/(lnx)))∫dx}dx −∫(1/(ln^2 x))dx I = (x/(lnx)) − ∫{((−1)/(ln^2 x)).(1/x).x}dx −∫(1/(ln^2 x))dx I = (x/(lnx)) + ∫{(1/(ln^2 x))dx −∫(1/(ln^2 x))dx I = (x/(lnx)) + c

$$\mathrm{I}\:=\:\int\frac{\mathrm{1}}{\mathrm{lnx}}\mathrm{dx}\:−\:\int\frac{\mathrm{1}}{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}\mathrm{dx} \\ $$$$\:\mathrm{Using}\:\mathrm{byparts},\: \\ $$$$\:\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{lnx}}\int\mathrm{dx}\:−\:\int\left\{\frac{\mathrm{d}}{\mathrm{dx}}\left(\frac{\mathrm{1}}{\mathrm{lnx}}\right)\int\mathrm{dx}\right\}\mathrm{dx}\:−\int\frac{\mathrm{1}}{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}\mathrm{dx} \\ $$$$\:\mathrm{I}\:=\:\frac{\mathrm{x}}{\mathrm{lnx}}\:\:−\:\int\left\{\frac{−\mathrm{1}}{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}.\frac{\mathrm{1}}{\mathrm{x}}.\mathrm{x}\right\}\mathrm{dx}\:−\int\frac{\mathrm{1}}{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}\mathrm{dx} \\ $$$$\:\mathrm{I}\:=\:\frac{\mathrm{x}}{\mathrm{lnx}}\:\:+\:\int\left\{\frac{\mathrm{1}}{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}\:−\int\frac{\mathrm{1}}{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}\right. \\ $$$$\:\mathrm{I}\:=\:\frac{\mathrm{x}}{\mathrm{lnx}}\:\:+\:\mathrm{c} \\ $$

Answered by Lordose last updated on 31/Oct/20

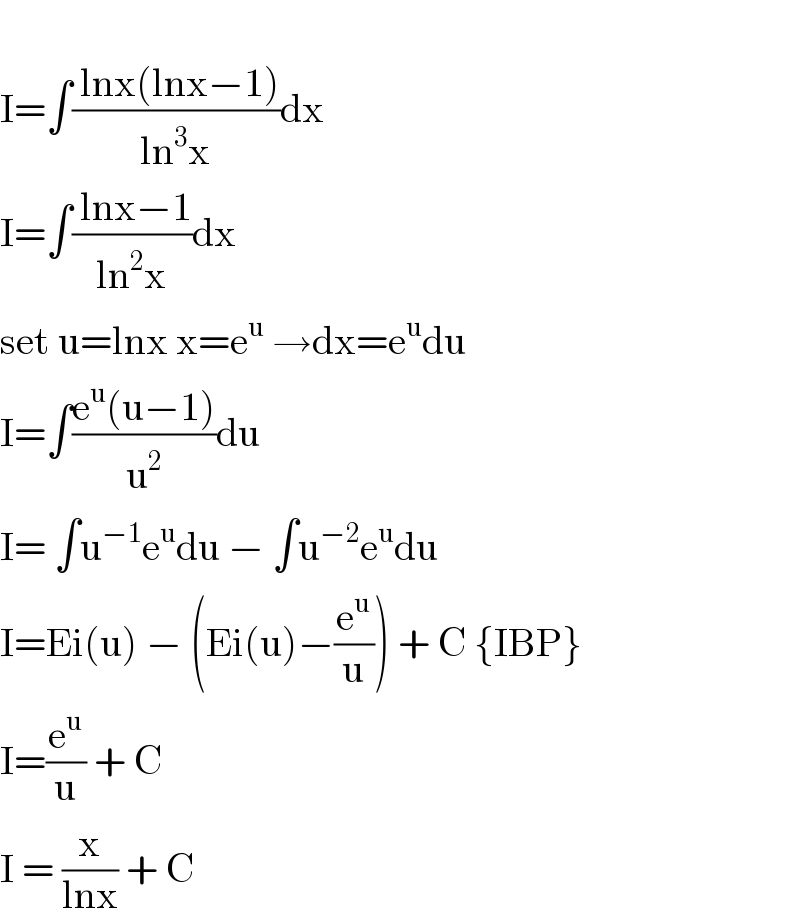
I=∫(( lnx(lnx−1))/(ln^3 x))dx I=∫(( lnx−1)/(ln^2 x))dx set u=lnx x=e^u →dx=e^u du I=∫((e^u (u−1))/u^2 )du I= ∫u^(−1) e^u du − ∫u^(−2) e^u du I=Ei(u) − (Ei(u)−(e^u /u)) + C {IBP} I=(e^u /u) + C I = (x/(lnx)) + C

$$ \\ $$$$\mathrm{I}=\int\frac{\:\mathrm{lnx}\left(\mathrm{lnx}−\mathrm{1}\right)}{\mathrm{ln}^{\mathrm{3}} \mathrm{x}}\mathrm{dx} \\ $$$$\mathrm{I}=\int\frac{\:\mathrm{lnx}−\mathrm{1}}{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}\mathrm{dx} \\ $$$$\mathrm{set}\:\mathrm{u}=\mathrm{lnx}\:\mathrm{x}=\mathrm{e}^{\mathrm{u}} \:\rightarrow\mathrm{dx}=\mathrm{e}^{\mathrm{u}} \mathrm{du} \\ $$$$\mathrm{I}=\int\frac{\mathrm{e}^{\mathrm{u}} \left(\mathrm{u}−\mathrm{1}\right)}{\mathrm{u}^{\mathrm{2}} }\mathrm{du} \\ $$$$\mathrm{I}=\:\int\mathrm{u}^{−\mathrm{1}} \mathrm{e}^{\mathrm{u}} \mathrm{du}\:−\:\int\mathrm{u}^{−\mathrm{2}} \mathrm{e}^{\mathrm{u}} \mathrm{du} \\ $$$$\mathrm{I}=\mathrm{Ei}\left(\mathrm{u}\right)\:−\:\left(\mathrm{Ei}\left(\mathrm{u}\right)−\frac{\mathrm{e}^{\mathrm{u}} }{\mathrm{u}}\right)\:+\:\mathrm{C}\:\left\{\mathrm{IBP}\right\} \\ $$$$\mathrm{I}=\frac{\mathrm{e}^{\mathrm{u}} }{\mathrm{u}}\:+\:\mathrm{C} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{x}}{\mathrm{lnx}}\:+\:\mathrm{C} \\ $$

Commented by SOMEDAVONG last updated on 31/Oct/20

(Thank you so much)

$$\left(\mathrm{Thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\right) \\ $$

Answered by TANMAY PANACEA last updated on 31/Oct/20

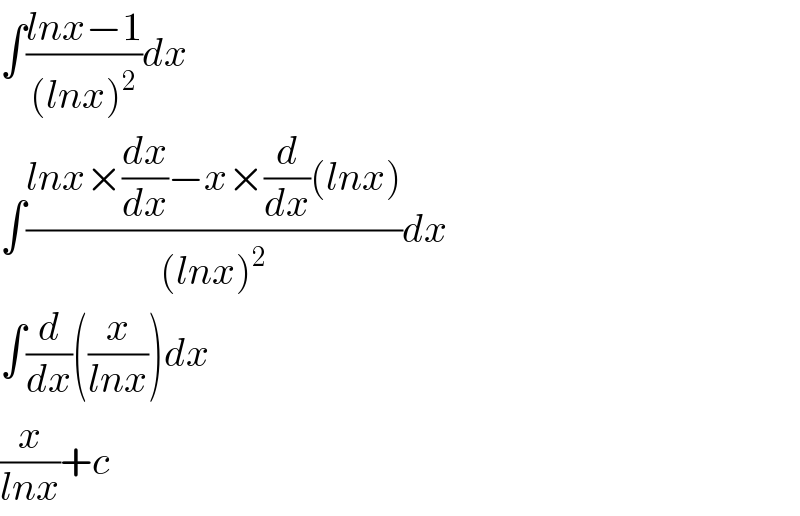
∫((lnx−1)/((lnx)^2 ))dx ∫((lnx×(dx/dx)−x×(d/dx)(lnx))/((lnx)^2 ))dx ∫(d/dx)((x/(lnx)))dx (x/(lnx))+c

$$\int\frac{{lnx}−\mathrm{1}}{\left({lnx}\right)^{\mathrm{2}} }{dx} \\ $$$$\int\frac{{lnx}×\frac{{dx}}{{dx}}−{x}×\frac{{d}}{{dx}}\left({lnx}\right)}{\left({lnx}\right)^{\mathrm{2}} }{dx} \\ $$$$\int\frac{{d}}{{dx}}\left(\frac{{x}}{{lnx}}\right){dx} \\ $$$$\frac{{x}}{{lnx}}+{c} \\ $$

Commented by mnjuly1970 last updated on 31/Oct/20

very nice solution sir tanmay .thank you...

$${very}\:{nice}\:{solution}\: \\ $$$${sir}\:\:{tanmay}\:.{thank}\:{you}... \\ $$

Commented by TANMAY PANACEA last updated on 31/Oct/20

most welcome sir

$${most}\:{welcome}\:{sir} \\ $$

Answered by mathmax by abdo last updated on 31/Oct/20

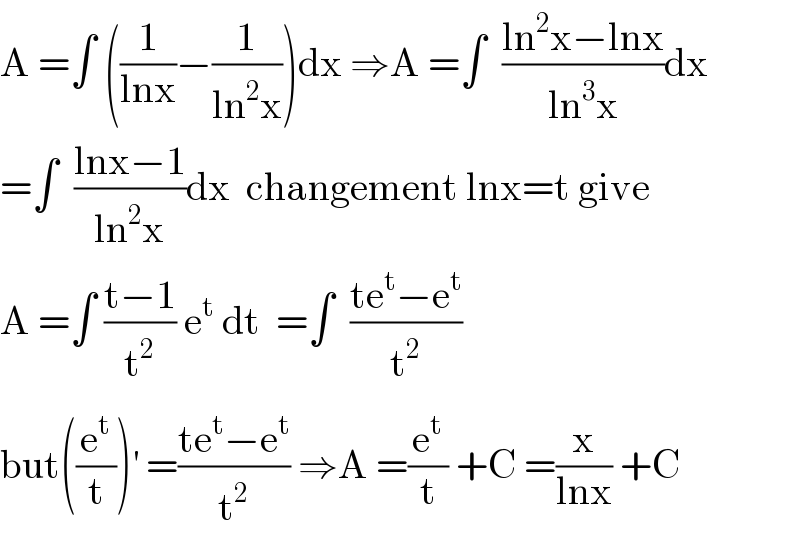
A =∫ ((1/(lnx))−(1/(ln^2 x)))dx ⇒A =∫ ((ln^2 x−lnx)/(ln^3 x))dx =∫ ((lnx−1)/(ln^2 x))dx changement lnx=t give A =∫ ((t−1)/t^2 ) e^t dt =∫ ((te^t −e^t )/t^2 ) but((e^t /t))^′ =((te^t −e^t )/t^2 ) ⇒A =(e^t /t) +C =(x/(lnx)) +C

$$\mathrm{A}\:=\int\:\left(\frac{\mathrm{1}}{\mathrm{lnx}}−\frac{\mathrm{1}}{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}\right)\mathrm{dx}\:\Rightarrow\mathrm{A}\:=\int\:\:\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{x}−\mathrm{lnx}}{\mathrm{ln}^{\mathrm{3}} \mathrm{x}}\mathrm{dx} \\ $$$$=\int\:\:\frac{\mathrm{lnx}−\mathrm{1}}{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{lnx}=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{A}\:=\int\:\frac{\mathrm{t}−\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\:\mathrm{e}^{\mathrm{t}} \:\mathrm{dt}\:\:=\int\:\:\frac{\mathrm{te}^{\mathrm{t}} −\mathrm{e}^{\mathrm{t}} }{\mathrm{t}^{\mathrm{2}} } \\ $$$$\mathrm{but}\left(\frac{\mathrm{e}^{\mathrm{t}} }{\mathrm{t}}\right)^{'} \:=\frac{\mathrm{te}^{\mathrm{t}} −\mathrm{e}^{\mathrm{t}} }{\mathrm{t}^{\mathrm{2}} }\:\Rightarrow\mathrm{A}\:=\frac{\mathrm{e}^{\mathrm{t}} }{\mathrm{t}}\:+\mathrm{C}\:=\frac{\mathrm{x}}{\mathrm{lnx}}\:+\mathrm{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com