Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 120463 by bramlexs22 last updated on 31/Oct/20

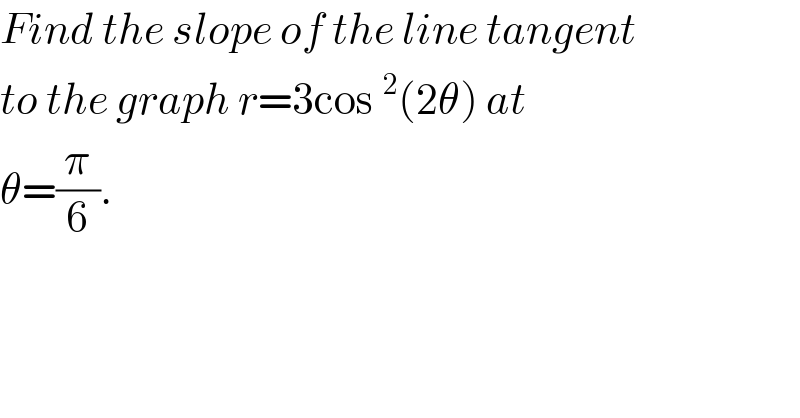
Find the slope of the line tangent to the graph r=3cos^2 (2θ) at θ=(π/6).

$${Find}\:{the}\:{slope}\:{of}\:{the}\:{line}\:{tangent} \\ $$$${to}\:{the}\:{graph}\:{r}=\mathrm{3cos}\:^{\mathrm{2}} \left(\mathrm{2}\theta\right)\:{at} \\ $$$$\theta=\frac{\pi}{\mathrm{6}}.\: \\ $$

Answered by mr W last updated on 31/Oct/20

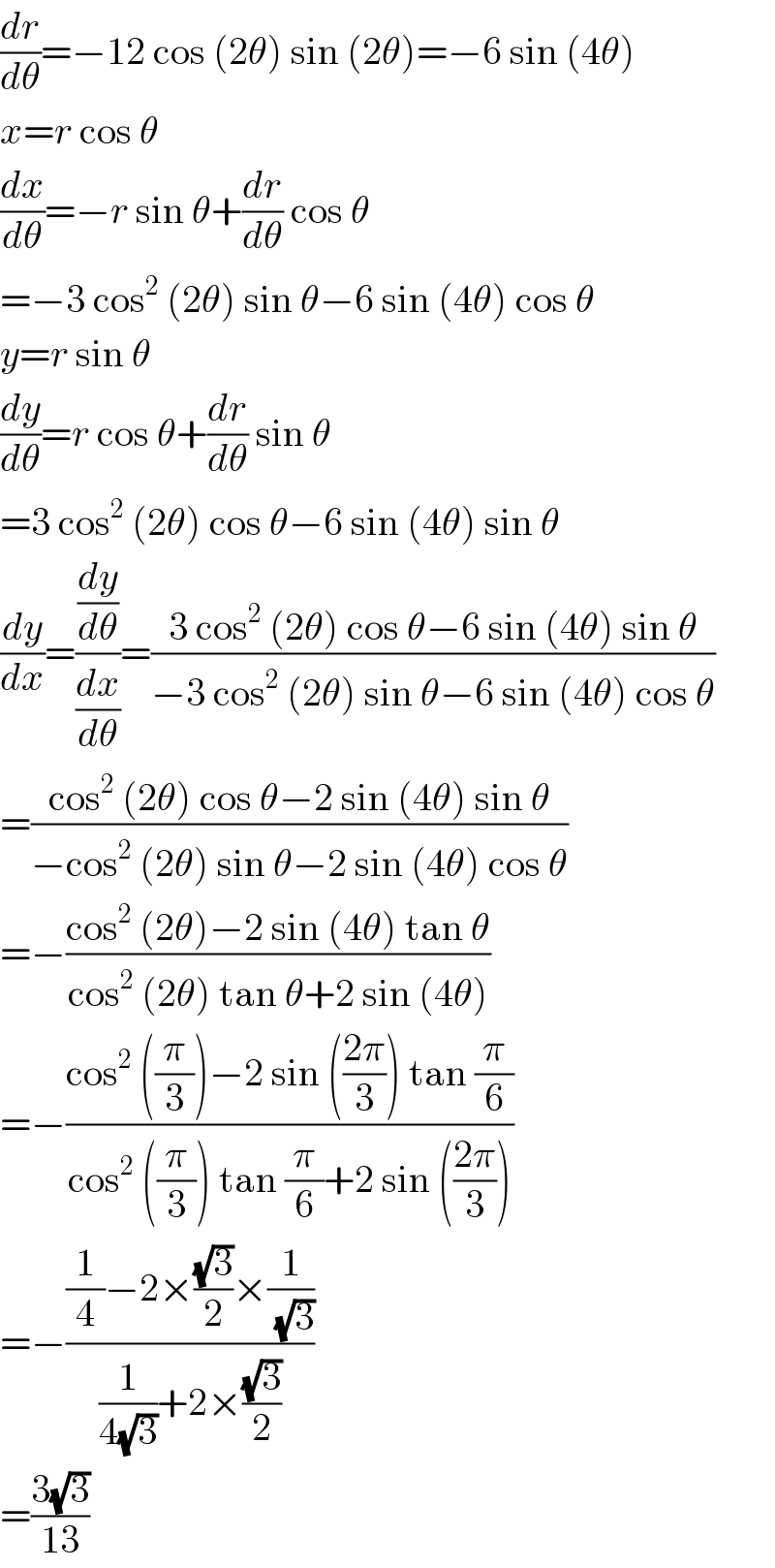
(dr/dθ)=−12 cos (2θ) sin (2θ)=−6 sin (4θ) x=r cos θ (dx/dθ)=−r sin θ+(dr/dθ) cos θ =−3 cos^2 (2θ) sin θ−6 sin (4θ) cos θ y=r sin θ (dy/dθ)=r cos θ+(dr/dθ) sin θ =3 cos^2 (2θ) cos θ−6 sin (4θ) sin θ (dy/dx)=((dy/dθ)/(dx/dθ))=((3 cos^2 (2θ) cos θ−6 sin (4θ) sin θ)/(−3 cos^2 (2θ) sin θ−6 sin (4θ) cos θ)) =((cos^2 (2θ) cos θ−2 sin (4θ) sin θ)/(−cos^2 (2θ) sin θ−2 sin (4θ) cos θ)) =−((cos^2 (2θ)−2 sin (4θ) tan θ)/(cos^2 (2θ) tan θ+2 sin (4θ))) =−((cos^2 ((π/3))−2 sin (((2π)/3)) tan (π/6))/(cos^2 ((π/3)) tan (π/6)+2 sin (((2π)/3)))) =−(((1/4)−2×((√3)/2)×(1/( (√3))))/((1/(4(√3)))+2×((√3)/2))) =((3(√3))/(13))

$$\frac{{dr}}{{d}\theta}=−\mathrm{12}\:\mathrm{cos}\:\left(\mathrm{2}\theta\right)\:\mathrm{sin}\:\left(\mathrm{2}\theta\right)=−\mathrm{6}\:\mathrm{sin}\:\left(\mathrm{4}\theta\right) \\ $$$${x}={r}\:\mathrm{cos}\:\theta \\ $$$$\frac{{dx}}{{d}\theta}=−{r}\:\mathrm{sin}\:\theta+\frac{{dr}}{{d}\theta}\:\mathrm{cos}\:\theta \\ $$$$=−\mathrm{3}\:\mathrm{cos}^{\mathrm{2}} \:\left(\mathrm{2}\theta\right)\:\mathrm{sin}\:\theta−\mathrm{6}\:\mathrm{sin}\:\left(\mathrm{4}\theta\right)\:\mathrm{cos}\:\theta \\ $$$${y}={r}\:\mathrm{sin}\:\theta \\ $$$$\frac{{dy}}{{d}\theta}={r}\:\mathrm{cos}\:\theta+\frac{{dr}}{{d}\theta}\:\mathrm{sin}\:\theta \\ $$$$=\mathrm{3}\:\mathrm{cos}^{\mathrm{2}} \:\left(\mathrm{2}\theta\right)\:\mathrm{cos}\:\theta−\mathrm{6}\:\mathrm{sin}\:\left(\mathrm{4}\theta\right)\:\mathrm{sin}\:\theta \\ $$$$\frac{{dy}}{{dx}}=\frac{\frac{{dy}}{{d}\theta}}{\frac{{dx}}{{d}\theta}}=\frac{\mathrm{3}\:\mathrm{cos}^{\mathrm{2}} \:\left(\mathrm{2}\theta\right)\:\mathrm{cos}\:\theta−\mathrm{6}\:\mathrm{sin}\:\left(\mathrm{4}\theta\right)\:\mathrm{sin}\:\theta}{−\mathrm{3}\:\mathrm{cos}^{\mathrm{2}} \:\left(\mathrm{2}\theta\right)\:\mathrm{sin}\:\theta−\mathrm{6}\:\mathrm{sin}\:\left(\mathrm{4}\theta\right)\:\mathrm{cos}\:\theta} \\ $$$$=\frac{\mathrm{cos}^{\mathrm{2}} \:\left(\mathrm{2}\theta\right)\:\mathrm{cos}\:\theta−\mathrm{2}\:\mathrm{sin}\:\left(\mathrm{4}\theta\right)\:\mathrm{sin}\:\theta}{−\mathrm{cos}^{\mathrm{2}} \:\left(\mathrm{2}\theta\right)\:\mathrm{sin}\:\theta−\mathrm{2}\:\mathrm{sin}\:\left(\mathrm{4}\theta\right)\:\mathrm{cos}\:\theta} \\ $$$$=−\frac{\mathrm{cos}^{\mathrm{2}} \:\left(\mathrm{2}\theta\right)−\mathrm{2}\:\mathrm{sin}\:\left(\mathrm{4}\theta\right)\:\mathrm{tan}\:\theta}{\mathrm{cos}^{\mathrm{2}} \:\left(\mathrm{2}\theta\right)\:\mathrm{tan}\:\theta+\mathrm{2}\:\mathrm{sin}\:\left(\mathrm{4}\theta\right)} \\ $$$$=−\frac{\mathrm{cos}^{\mathrm{2}} \:\left(\frac{\pi}{\mathrm{3}}\right)−\mathrm{2}\:\mathrm{sin}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\:\mathrm{tan}\:\frac{\pi}{\mathrm{6}}}{\mathrm{cos}^{\mathrm{2}} \:\left(\frac{\pi}{\mathrm{3}}\right)\:\mathrm{tan}\:\frac{\pi}{\mathrm{6}}+\mathrm{2}\:\mathrm{sin}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)} \\ $$$$=−\frac{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{2}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}{\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{3}}}+\mathrm{2}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{13}} \\ $$

Commented by mr W last updated on 31/Oct/20

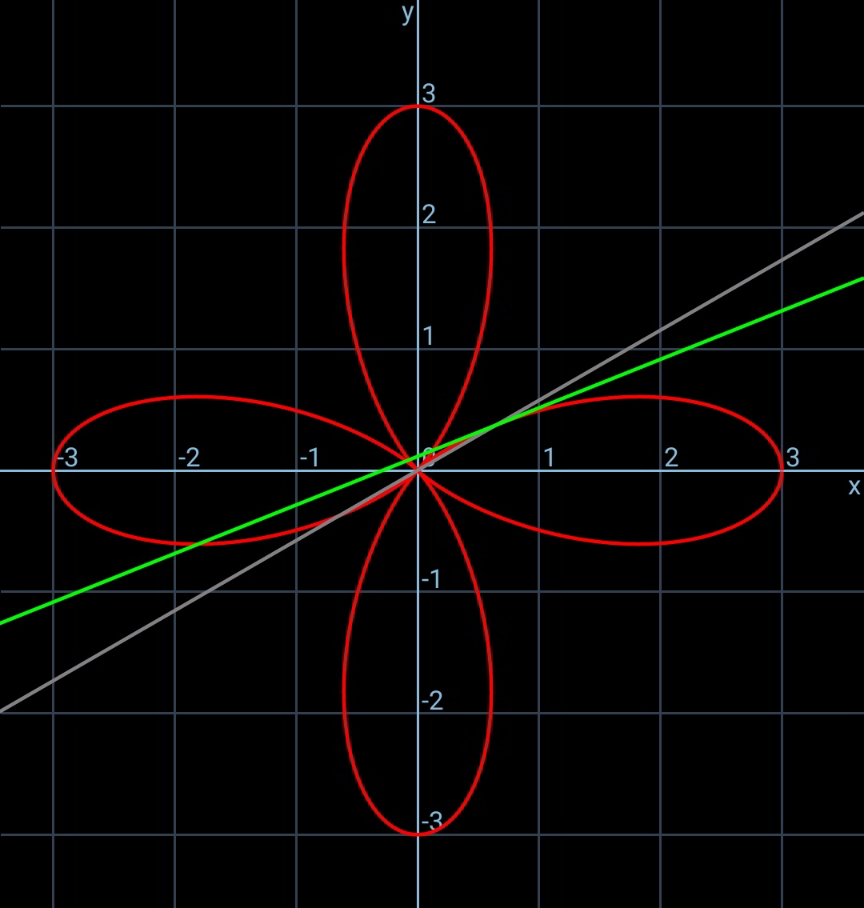
Answered by john santu last updated on 01/Nov/20

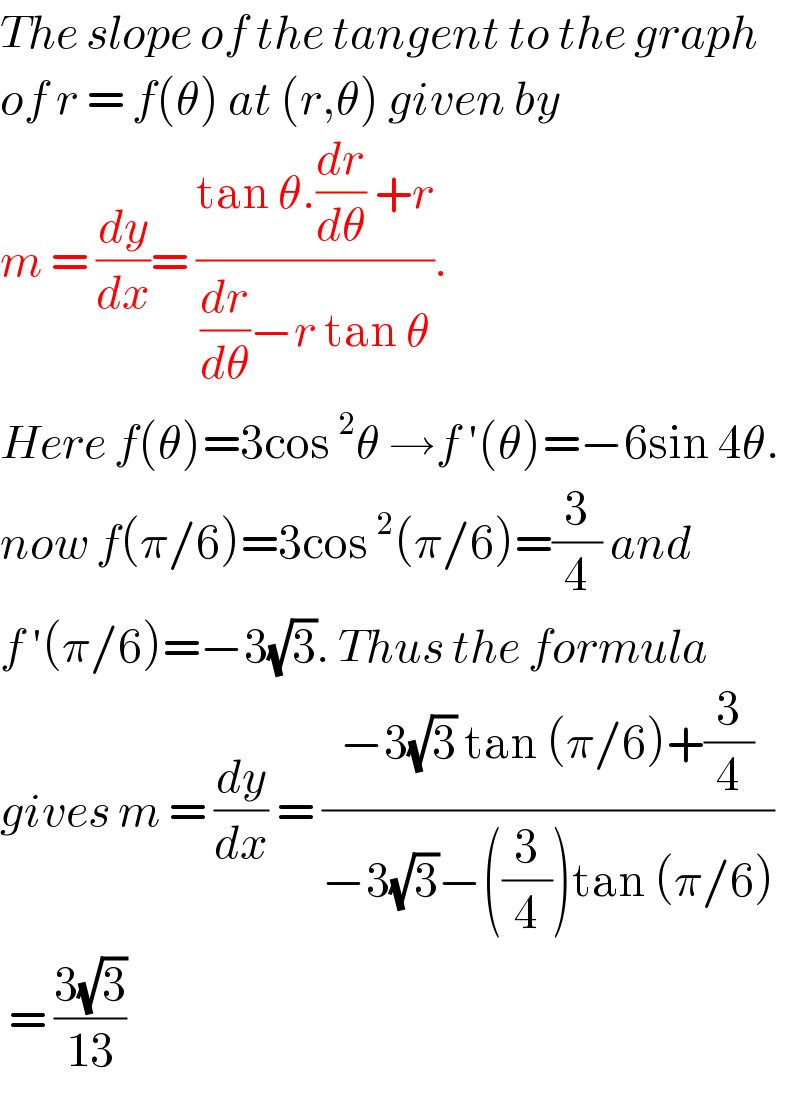
The slope of the tangent to the graph of r = f(θ) at (r,θ) given by m = (dy/dx)= ((tan θ.(dr/dθ) +r)/((dr/dθ)−r tan θ)). Here f(θ)=3cos^2 θ →f ′(θ)=−6sin 4θ. now f(π/6)=3cos^2 (π/6)=(3/4) and f ′(π/6)=−3(√3). Thus the formula gives m = (dy/dx) = ((−3(√3) tan (π/6)+(3/4))/(−3(√3)−((3/4))tan (π/6))) = ((3(√3))/(13))

$${The}\:{slope}\:{of}\:{the}\:{tangent}\:{to}\:{the}\:{graph} \\ $$$${of}\:{r}\:=\:{f}\left(\theta\right)\:{at}\:\left({r},\theta\right)\:{given}\:{by}\: \\ $$$${m}\:=\:\frac{{dy}}{{dx}}=\:\frac{\mathrm{tan}\:\theta.\frac{{dr}}{{d}\theta}\:+{r}}{\frac{{dr}}{{d}\theta}−{r}\:\mathrm{tan}\:\theta}. \\ $$$${Here}\:{f}\left(\theta\right)=\mathrm{3cos}\:^{\mathrm{2}} \theta\:\rightarrow{f}\:'\left(\theta\right)=−\mathrm{6sin}\:\mathrm{4}\theta. \\ $$$${now}\:{f}\left(\pi/\mathrm{6}\right)=\mathrm{3cos}\:^{\mathrm{2}} \left(\pi/\mathrm{6}\right)=\frac{\mathrm{3}}{\mathrm{4}}\:{and}\: \\ $$$${f}\:'\left(\pi/\mathrm{6}\right)=−\mathrm{3}\sqrt{\mathrm{3}}.\:{Thus}\:{the}\:{formula} \\ $$$${gives}\:{m}\:=\:\frac{{dy}}{{dx}}\:=\:\frac{−\mathrm{3}\sqrt{\mathrm{3}}\:\mathrm{tan}\:\left(\pi/\mathrm{6}\right)+\frac{\mathrm{3}}{\mathrm{4}}}{−\mathrm{3}\sqrt{\mathrm{3}}−\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\mathrm{tan}\:\left(\pi/\mathrm{6}\right)} \\ $$$$\:=\:\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{13}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com