Question and Answers Forum

All Questions      Topic List

Mensuration Questions

Previous in All Question      Next in All Question      

Previous in Mensuration      Next in Mensuration      

Question Number 121793 by ajfour last updated on 11/Nov/20

Commented by ajfour last updated on 13/Nov/20

If ODE^(⌢) is a sector, and △ABC is equilateral with minimum area has an area equal to △OEF , find θ.

$${If}\:{O}\overset{\frown} {{DE}}\:\:\:{is}\:{a}\:{sector},\:{and}\:\bigtriangleup{ABC}\: \\ $$$${is}\:{equilateral}\:{with}\:{minimum}\:{area} \\ $$$${has}\:{an}\:{area}\:{equal}\:{to}\:\bigtriangleup{OEF}\:,\:{find}\:\theta. \\ $$$$ \\ $$

Commented by ajfour last updated on 14/Nov/20

mrW Sir kindly help with this Q.

$${mrW}\:{Sir}\:{kindly}\:{help}\:{with}\:{this}\:{Q}. \\ $$

Answered by ajfour last updated on 13/Nov/20

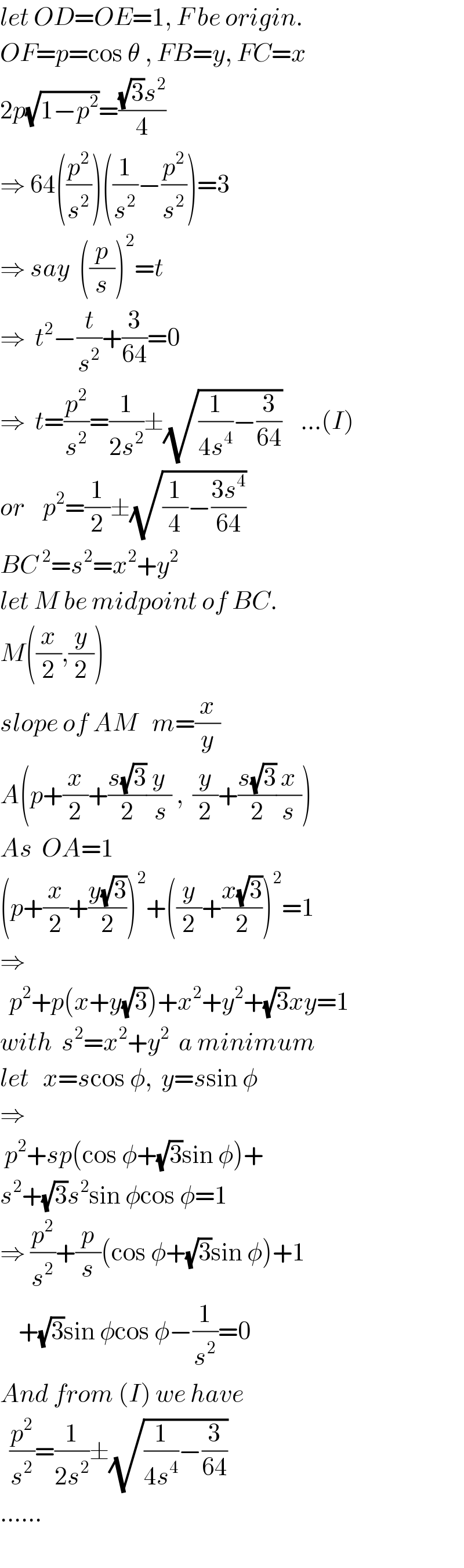
let OD=OE=1, F be origin. OF=p=cos θ , FB=y, FC=x 2p(√(1−p^2 ))=(((√3)s^2 )/4) ⇒ 64((p^2 /s^2 ))((1/s^2 )−(p^2 /s^2 ))=3 ⇒ say ((p/s))^2 =t ⇒ t^2 −(t/s^2 )+(3/(64))=0 ⇒ t=(p^2 /s^2 )=(1/(2s^2 ))±(√((1/(4s^4 ))−(3/(64)))) ...(I) or p^2 =(1/2)±(√((1/4)−((3s^4 )/(64)))) BC^( 2) =s^2 =x^2 +y^2 let M be midpoint of BC. M((x/2),(y/2)) slope of AM m=(x/y) A(p+(x/2)+((s(√3))/2)(y/( s)) , (y/2)+((s(√3))/2)(x/s)) As OA=1 (p+(x/2)+((y(√3))/2))^2 +((y/2)+((x(√3))/2))^2 =1 ⇒ p^2 +p(x+y(√3))+x^2 +y^2 +(√3)xy=1 with s^2 =x^2 +y^2 a minimum let x=scos φ, y=ssin φ ⇒ p^2 +sp(cos φ+(√3)sin φ)+ s^2 +(√3)s^2 sin φcos φ=1 ⇒ (p^2 /s^2 )+(p/s)(cos φ+(√3)sin φ)+1 +(√3)sin φcos φ−(1/s^2 )=0 And from (I) we have (p^2 /s^2 )=(1/(2s^2 ))±(√((1/(4s^4 ))−(3/(64)))) ......

$${let}\:{OD}={OE}=\mathrm{1},\:{F}\:{be}\:{origin}. \\ $$$${OF}={p}=\mathrm{cos}\:\theta\:,\:{FB}={y},\:{FC}={x} \\ $$$$\mathrm{2}{p}\sqrt{\mathrm{1}−{p}^{\mathrm{2}} }=\frac{\sqrt{\mathrm{3}}{s}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\Rightarrow\:\mathrm{64}\left(\frac{{p}^{\mathrm{2}} }{{s}^{\mathrm{2}} }\right)\left(\frac{\mathrm{1}}{{s}^{\mathrm{2}} }−\frac{{p}^{\mathrm{2}} }{{s}^{\mathrm{2}} }\right)=\mathrm{3} \\ $$$$\Rightarrow\:{say}\:\:\left(\frac{{p}}{{s}}\right)^{\mathrm{2}} ={t} \\ $$$$\Rightarrow\:\:{t}^{\mathrm{2}} −\frac{{t}}{{s}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{64}}=\mathrm{0} \\ $$$$\Rightarrow\:\:{t}=\frac{{p}^{\mathrm{2}} }{{s}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}{s}^{\mathrm{2}} }\pm\sqrt{\frac{\mathrm{1}}{\mathrm{4}{s}^{\mathrm{4}} }−\frac{\mathrm{3}}{\mathrm{64}}}\:\:\:\:...\left({I}\right) \\ $$$${or}\:\:\:\:{p}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\pm\sqrt{\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{3}{s}^{\mathrm{4}} }{\mathrm{64}}} \\ $$$${BC}^{\:\mathrm{2}} ={s}^{\mathrm{2}} ={x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$${let}\:{M}\:{be}\:{midpoint}\:{of}\:{BC}. \\ $$$${M}\left(\frac{{x}}{\mathrm{2}},\frac{{y}}{\mathrm{2}}\right) \\ $$$${slope}\:{of}\:{AM}\:\:\:{m}=\frac{{x}}{{y}} \\ $$$${A}\left({p}+\frac{{x}}{\mathrm{2}}+\frac{{s}\sqrt{\mathrm{3}}}{\mathrm{2}}\frac{{y}}{\:{s}}\:,\:\:\frac{{y}}{\mathrm{2}}+\frac{{s}\sqrt{\mathrm{3}}}{\mathrm{2}}\frac{{x}}{{s}}\right) \\ $$$${As}\:\:{OA}=\mathrm{1} \\ $$$$\left({p}+\frac{{x}}{\mathrm{2}}+\frac{{y}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{{y}}{\mathrm{2}}+\frac{{x}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow \\ $$$$\:\:{p}^{\mathrm{2}} +{p}\left({x}+{y}\sqrt{\mathrm{3}}\right)+{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\sqrt{\mathrm{3}}{xy}=\mathrm{1} \\ $$$${with}\:\:{s}^{\mathrm{2}} ={x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:\:{a}\:{minimum} \\ $$$${let}\:\:\:{x}={s}\mathrm{cos}\:\phi,\:\:{y}={s}\mathrm{sin}\:\phi \\ $$$$\Rightarrow \\ $$$$\:{p}^{\mathrm{2}} +{sp}\left(\mathrm{cos}\:\phi+\sqrt{\mathrm{3}}\mathrm{sin}\:\phi\right)+ \\ $$$${s}^{\mathrm{2}} +\sqrt{\mathrm{3}}{s}^{\mathrm{2}} \mathrm{sin}\:\phi\mathrm{cos}\:\phi=\mathrm{1} \\ $$$$\Rightarrow\:\frac{{p}^{\mathrm{2}} }{{s}^{\mathrm{2}} }+\frac{{p}}{{s}}\left(\mathrm{cos}\:\phi+\sqrt{\mathrm{3}}\mathrm{sin}\:\phi\right)+\mathrm{1} \\ $$$$\:\:\:\:+\sqrt{\mathrm{3}}\mathrm{sin}\:\phi\mathrm{cos}\:\phi−\frac{\mathrm{1}}{{s}^{\mathrm{2}} }=\mathrm{0} \\ $$$${And}\:{from}\:\left({I}\right)\:{we}\:{have} \\ $$$$\:\:\frac{{p}^{\mathrm{2}} }{{s}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}{s}^{\mathrm{2}} }\pm\sqrt{\frac{\mathrm{1}}{\mathrm{4}{s}^{\mathrm{4}} }−\frac{\mathrm{3}}{\mathrm{64}}}\: \\ $$$$...... \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com