
Question Number 123393 by malwan last updated on 25/Nov/20
![find the equations of [two] circles which thier center both (2,−2) and tangent with circle x^2 + y^2 −8x + 10y + 5 = 0](Q123393.png)
$${find}\:{the}\:{equations}\:{of}\:\left[{two}\right]\:{circles} \\ $$$${which}\:{thier}\:{center}\:{both}\:\left(\mathrm{2},−\mathrm{2}\right) \\ $$$${and}\:{tangent}\:{with}\:{circle} \\ $$$${x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} \:−\mathrm{8}{x}\:+\:\mathrm{10}{y}\:+\:\mathrm{5}\:=\:\mathrm{0} \\ $$
Commented by malwan last updated on 25/Nov/20
$${can}\:{you}\:{drow}\:{it}\:{sir}\:? \\ $$
Commented by MJS_new last updated on 25/Nov/20

$$\mathrm{sorry}\:\mathrm{I}\:\mathrm{have}\:\mathrm{no}\:\mathrm{drawing}\:\mathrm{app} \\ $$
Commented by talminator2856791 last updated on 25/Nov/20

$$\:\mathrm{you}\:\mathrm{can}\:\mathrm{use}\:\mathrm{this}\:\mathrm{app}\:\mathrm{drawing}\:\mathrm{tool} \\ $$
Commented by malwan last updated on 25/Nov/20

$${can}\:{you}\:{try}\:{sir}\:? \\ $$
Commented by MJS_new last updated on 25/Nov/20

$$\mathrm{sorry}\:\mathrm{I}\:\mathrm{never}\:\mathrm{used}\:\mathrm{it}\:\mathrm{and}\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{have}\:\mathrm{the}\:\mathrm{time} \\ $$$$\mathrm{to}\:\mathrm{get}\:\mathrm{used}\:\mathrm{to}\:\mathrm{it}.\:\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{sketch} \\ $$
Commented by talminator2856791 last updated on 25/Nov/20

$$\:\mathrm{yes}\:\mathrm{i}\:\mathrm{tried}\:\mathrm{but}\:\mathrm{it}\:\mathrm{is}\:\mathrm{difficult}\:\mathrm{to}\:\mathrm{use}\:\mathrm{this} \\ $$
Answered by talminator2856791 last updated on 25/Nov/20
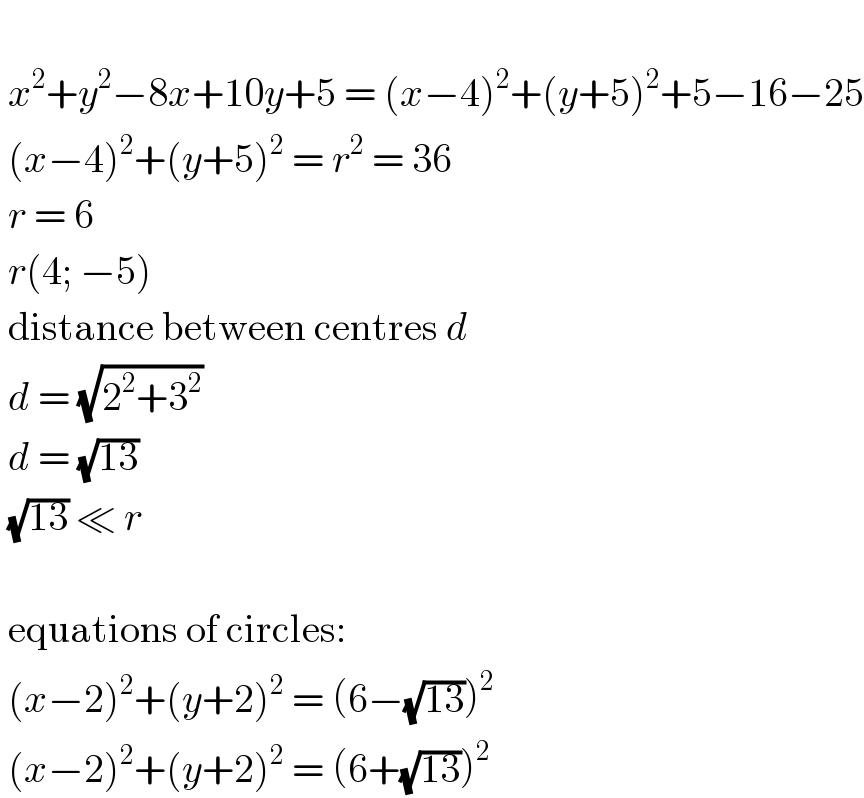
$$\: \\ $$$$\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{10}{y}+\mathrm{5}\:=\:\left({x}−\mathrm{4}\right)^{\mathrm{2}} +\left({y}+\mathrm{5}\right)^{\mathrm{2}} +\mathrm{5}−\mathrm{16}−\mathrm{25} \\ $$$$\:\left({x}−\mathrm{4}\right)^{\mathrm{2}} +\left({y}+\mathrm{5}\right)^{\mathrm{2}} \:=\:{r}^{\mathrm{2}} \:=\:\mathrm{36} \\ $$$$\:{r}\:=\:\mathrm{6} \\ $$$$\:{r}\left(\mathrm{4};\:−\mathrm{5}\right) \\ $$$$\:\mathrm{distance}\:\mathrm{between}\:\mathrm{centres}\:{d} \\ $$$$\:{d}\:=\:\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} } \\ $$$$\:{d}\:=\:\sqrt{\mathrm{13}} \\ $$$$\:\sqrt{\mathrm{13}}\:\ll\:{r} \\ $$$$\: \\ $$$$\:\mathrm{equations}\:\mathrm{of}\:\mathrm{circles}: \\ $$$$\:\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\left({y}+\mathrm{2}\right)^{\mathrm{2}} \:=\:\left(\mathrm{6}−\sqrt{\mathrm{13}}\right)^{\mathrm{2}} \\ $$$$\:\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\left({y}+\mathrm{2}\right)^{\mathrm{2}} \:=\:\left(\mathrm{6}+\sqrt{\mathrm{13}}\right)^{\mathrm{2}} \\ $$
Commented by malwan last updated on 25/Nov/20

$${thank}\:{you}\:{sir} \\ $$
Answered by MJS_new last updated on 25/Nov/20
![(1) (x−2)^2 +(y+2)^2 −r^2 =0 (2) x^2 +y^2 −8x+10y+5=0 (1) x^2 +y^2 −4x+4y+8−r^2 =0 (1)−(2) 4x−6y+3−r^2 =0 ⇒ y=((4x−r^2 +3)/6) insert in (1) or (2) ((13)/9)x^2 −((2(r^2 +3))/9)+((r^4 −66r^2 +369)/(36))=0 x^2 −((2(o^2 +3))/(13))x+((r^4 −66r^2 +369)/(52))=0 tangenting circles means we must find r in order to get a? double solution for x x^2 +px+q=0 ⇒ x=−(p/2)±(√((p^2 /4)−q)) we need (p^2 /4)−q=0 ⇒ (9/(676))(r^4 −98r^2 +529)=0 ⇒ r=6±(√(13)) [r>0] ⇒ circle 1: (x−2)^2 +(y+2)^2 +49−12(√(13))=0 circle 2: (x−2)^2 +(y+2)^2 +49+12(√(13))=0](Q123400.png)
$$\left(\mathrm{1}\right)\:\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\left({y}+\mathrm{2}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\mathrm{2}\right)\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{10}{y}+\mathrm{5}=\mathrm{0} \\ $$$$\left(\mathrm{1}\right)\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}{y}+\mathrm{8}−{r}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\mathrm{1}\right)−\left(\mathrm{2}\right)\:\mathrm{4}{x}−\mathrm{6}{y}+\mathrm{3}−{r}^{\mathrm{2}} =\mathrm{0}\:\Rightarrow\:{y}=\frac{\mathrm{4}{x}−{r}^{\mathrm{2}} +\mathrm{3}}{\mathrm{6}} \\ $$$$\mathrm{insert}\:\mathrm{in}\:\left(\mathrm{1}\right)\:\mathrm{or}\:\left(\mathrm{2}\right) \\ $$$$\frac{\mathrm{13}}{\mathrm{9}}{x}^{\mathrm{2}} −\frac{\mathrm{2}\left({r}^{\mathrm{2}} +\mathrm{3}\right)}{\mathrm{9}}+\frac{{r}^{\mathrm{4}} −\mathrm{66}{r}^{\mathrm{2}} +\mathrm{369}}{\mathrm{36}}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\frac{\mathrm{2}\left({o}^{\mathrm{2}} +\mathrm{3}\right)}{\mathrm{13}}{x}+\frac{{r}^{\mathrm{4}} −\mathrm{66}{r}^{\mathrm{2}} +\mathrm{369}}{\mathrm{52}}=\mathrm{0} \\ $$$$\mathrm{tangenting}\:\mathrm{circles}\:\mathrm{means}\:\mathrm{we}\:\mathrm{must}\:\mathrm{find}\:{r}\:\mathrm{in} \\ $$$$\mathrm{order}\:\mathrm{to}\:\mathrm{get}\:\mathrm{a}?\:\mathrm{double}\:\mathrm{solution}\:\mathrm{for}\:{x} \\ $$$${x}^{\mathrm{2}} +{px}+{q}=\mathrm{0}\:\Rightarrow\:{x}=−\frac{{p}}{\mathrm{2}}\pm\sqrt{\frac{{p}^{\mathrm{2}} }{\mathrm{4}}−{q}} \\ $$$$\mathrm{we}\:\mathrm{need}\:\frac{{p}^{\mathrm{2}} }{\mathrm{4}}−{q}=\mathrm{0} \\ $$$$\Rightarrow\:\frac{\mathrm{9}}{\mathrm{676}}\left({r}^{\mathrm{4}} −\mathrm{98}{r}^{\mathrm{2}} +\mathrm{529}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{r}=\mathrm{6}\pm\sqrt{\mathrm{13}}\:\left[{r}>\mathrm{0}\right] \\ $$$$\Rightarrow \\ $$$$\mathrm{circle}\:\mathrm{1}:\:\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\left({y}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{49}−\mathrm{12}\sqrt{\mathrm{13}}=\mathrm{0} \\ $$$$\mathrm{circle}\:\mathrm{2}:\:\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\left({y}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{49}+\mathrm{12}\sqrt{\mathrm{13}}=\mathrm{0} \\ $$
Commented by malwan last updated on 25/Nov/20
$${thank}\:{you}\:{so}\:{much}\:{sir} \\ $$
Commented by peter frank last updated on 25/Nov/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
