Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 124228 by mnjuly1970 last updated on 01/Dec/20

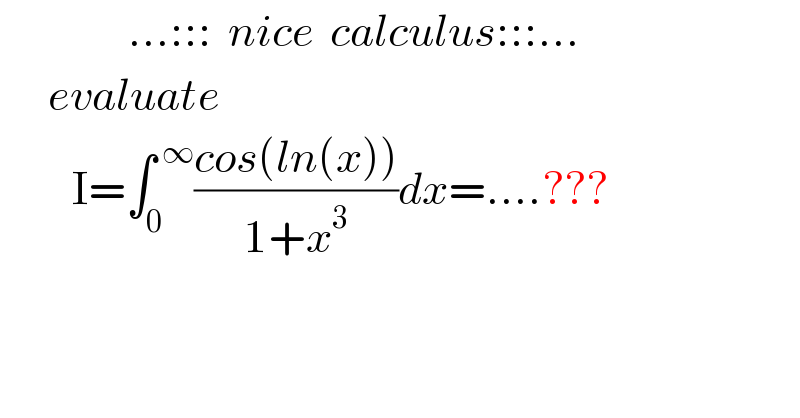
...::: nice calculus:::... evaluate I=∫_0 ^( ∞) ((cos(ln(x)))/(1+x^3 ))dx=....???

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:...:::\:\:{nice}\:\:{calculus}:::... \\ $$$$\:\:\:\:\:\:{evaluate} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{I}=\int_{\mathrm{0}} ^{\:\infty} \frac{{cos}\left({ln}\left({x}\right)\right)}{\mathrm{1}+{x}^{\mathrm{3}} }{dx}=....??? \\ $$

Answered by Lordose last updated on 01/Dec/20

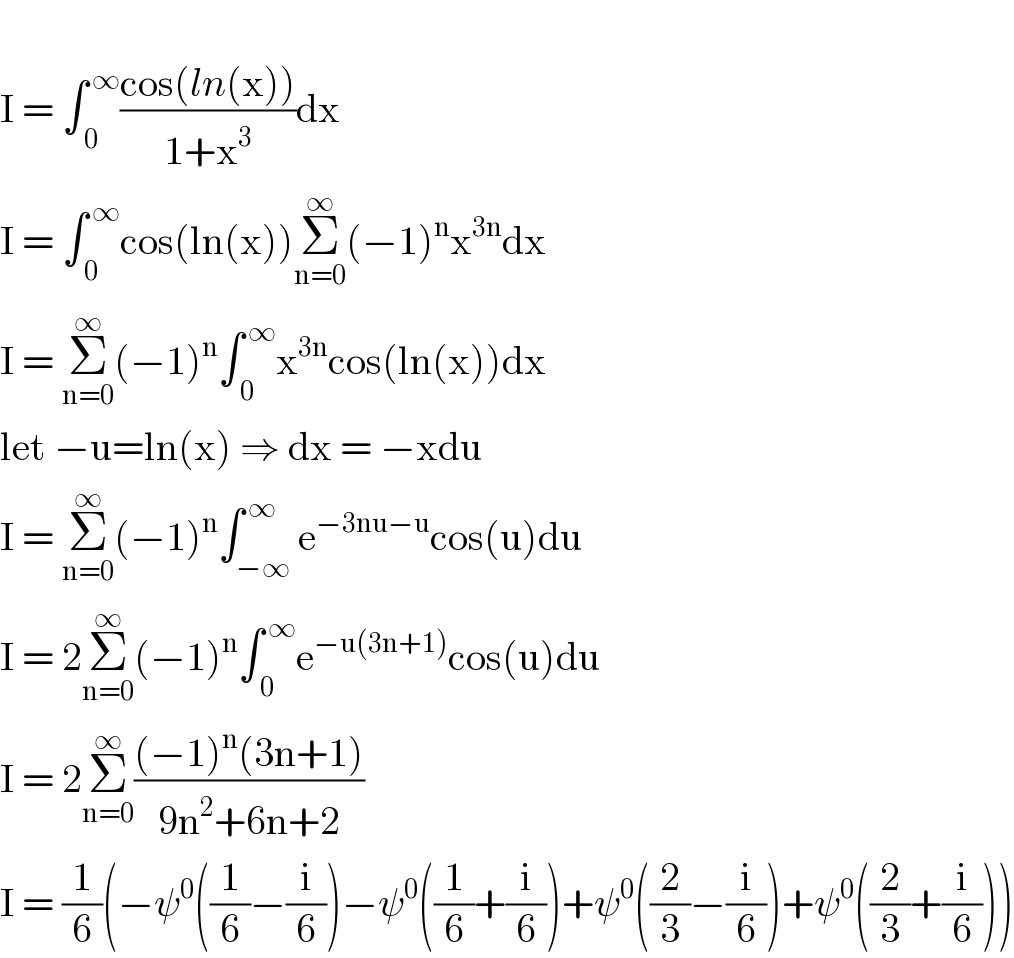
I = ∫_( 0) ^( ∞) ((cos(ln(x)))/(1+x^3 ))dx I = ∫_( 0) ^( ∞) cos(ln(x))Σ_(n=0) ^∞ (−1)^n x^(3n) dx I = Σ_(n=0) ^∞ (−1)^n ∫_( 0) ^( ∞) x^(3n) cos(ln(x))dx let −u=ln(x) ⇒ dx = −xdu I = Σ_(n=0) ^∞ (−1)^n ∫_(−∞) ^( ∞) e^(−3nu−u) cos(u)du I = 2Σ_(n=0) ^∞ (−1)^n ∫_( 0) ^( ∞) e^(−u(3n+1)) cos(u)du I = 2Σ_(n=0) ^∞ (((−1)^n (3n+1))/(9n^2 +6n+2)) I = (1/6)(−ψ^0 ((1/6)−(i/6))−ψ^0 ((1/6)+(i/6))+ψ^0 ((2/3)−(i/6))+ψ^0 ((2/3)+(i/6)))

$$ \\ $$$$\mathrm{I}\:=\:\int_{\:\mathrm{0}} ^{\:\infty} \frac{\mathrm{cos}\left({ln}\left(\mathrm{x}\right)\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }\mathrm{dx} \\ $$$$\mathrm{I}\:=\:\int_{\:\mathrm{0}} ^{\:\infty} \mathrm{cos}\left(\mathrm{ln}\left(\mathrm{x}\right)\right)\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{x}^{\mathrm{3n}} \mathrm{dx} \\ $$$$\mathrm{I}\:=\:\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}} \int_{\:\mathrm{0}} ^{\:\infty} \mathrm{x}^{\mathrm{3n}} \mathrm{cos}\left(\mathrm{ln}\left(\mathrm{x}\right)\right)\mathrm{dx} \\ $$$$\mathrm{let}\:−\mathrm{u}=\mathrm{ln}\left(\mathrm{x}\right)\:\Rightarrow\:\mathrm{dx}\:=\:−\mathrm{xdu} \\ $$$$\mathrm{I}\:=\:\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}} \int_{−\infty} ^{\:\infty} \mathrm{e}^{−\mathrm{3nu}−\mathrm{u}} \mathrm{cos}\left(\mathrm{u}\right)\mathrm{du} \\ $$$$\mathrm{I}\:=\:\mathrm{2}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}} \int_{\:\mathrm{0}} ^{\:\infty} \mathrm{e}^{−\mathrm{u}\left(\mathrm{3n}+\mathrm{1}\right)} \mathrm{cos}\left(\mathrm{u}\right)\mathrm{du} \\ $$$$\mathrm{I}\:=\:\mathrm{2}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\mathrm{3n}+\mathrm{1}\right)}{\mathrm{9n}^{\mathrm{2}} +\mathrm{6n}+\mathrm{2}} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{6}}\left(−\psi^{\mathrm{0}} \left(\frac{\mathrm{1}}{\mathrm{6}}−\frac{\mathrm{i}}{\mathrm{6}}\right)−\psi^{\mathrm{0}} \left(\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{i}}{\mathrm{6}}\right)+\psi^{\mathrm{0}} \left(\frac{\mathrm{2}}{\mathrm{3}}−\frac{\mathrm{i}}{\mathrm{6}}\right)+\psi^{\mathrm{0}} \left(\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{i}}{\mathrm{6}}\right)\right) \\ $$

Answered by mnjuly1970 last updated on 02/Dec/20

solution: I=Re(∫_0 ^( ∞) (e^(iln(x)) /(1+x^3 ))dx=Ω) Ω=∫_0 ^( ∞) (x^i /(1+x^3 ))dx=^((x^3 =t)) =(1/3)∫_0 ^( ∞) (t^((i−2)/3) /(1+t))dt =(1/3) Γ(((i+1)/3))Γ(1−((1+i)/3)) =(1/3)∗ (π/(sin((((i+1)π)/3)))) =(1/3)∗(π/(((√3)/2)cos(((πi)/3))+(1/2)sin(((πi)/3)))) =(2/3)[(π/( (√3)(((e^(−(π/3)) +e^(π/3) )/2))−i(((e^((−π)/3) −e^(π/3) )/2))))] =(4/3)((π/( (√3)cos(h((π/3)))+isin(h((π/3)))))) =((4π)/3){(((√3) cos(h((π/3)))−isin(h((π/3))) )/(3cos(h((π/3)))+sin(h((π/3)))))} I=Re(Ω)=((4π(√3))/3)(((cos(h((π/3))))/(3cos(h((π/3)))+sin(h((π/3)))))) =((4π(√3))/3)((1/(3+tan(h((π/3)))))) ✓

$${solution}: \\ $$$$\:\:\:\mathrm{I}={Re}\left(\int_{\mathrm{0}} ^{\:\infty} \frac{{e}^{{iln}\left({x}\right)} }{\mathrm{1}+{x}^{\mathrm{3}} }{dx}=\Omega\right) \\ $$$$\:\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\infty} \frac{{x}^{{i}} }{\mathrm{1}+{x}^{\mathrm{3}} }{dx}\overset{\left({x}^{\mathrm{3}} ={t}\right)} {=}=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\:\infty} \:\frac{{t}^{\frac{{i}−\mathrm{2}}{\mathrm{3}}} }{\mathrm{1}+{t}}{dt} \\ $$$$\:=\frac{\mathrm{1}}{\mathrm{3}}\:\Gamma\left(\frac{{i}+\mathrm{1}}{\mathrm{3}}\right)\Gamma\left(\mathrm{1}−\frac{\mathrm{1}+{i}}{\mathrm{3}}\right) \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{3}}\ast\:\frac{\pi}{{sin}\left(\frac{\left({i}+\mathrm{1}\right)\pi}{\mathrm{3}}\right)} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{3}}\ast\frac{\pi}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{cos}\left(\frac{\pi{i}}{\mathrm{3}}\right)+\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\frac{\pi{i}}{\mathrm{3}}\right)} \\ $$$$\:=\frac{\mathrm{2}}{\mathrm{3}}\left[\frac{\pi}{\:\sqrt{\mathrm{3}}\left(\frac{{e}^{−\frac{\pi}{\mathrm{3}}} +{e}^{\frac{\pi}{\mathrm{3}}} }{\mathrm{2}}\right)−{i}\left(\frac{{e}^{\frac{−\pi}{\mathrm{3}}} −{e}^{\frac{\pi}{\mathrm{3}}} }{\mathrm{2}}\right)}\right] \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\left(\frac{\pi}{\:\sqrt{\mathrm{3}}{cos}\left({h}\left(\frac{\pi}{\mathrm{3}}\right)\right)+{isin}\left({h}\left(\frac{\pi}{\mathrm{3}}\right)\right)}\right) \\ $$$$\:=\frac{\mathrm{4}\pi}{\mathrm{3}}\left\{\frac{\sqrt{\mathrm{3}}\:{cos}\left({h}\left(\frac{\pi}{\mathrm{3}}\right)\right)−{isin}\left({h}\left(\frac{\pi}{\mathrm{3}}\right)\right)\:\:\:}{\mathrm{3}{cos}\left({h}\left(\frac{\pi}{\mathrm{3}}\right)\right)+{sin}\left({h}\left(\frac{\pi}{\mathrm{3}}\right)\right)}\right\} \\ $$$$\mathrm{I}={Re}\left(\Omega\right)=\frac{\mathrm{4}\pi\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\frac{{cos}\left({h}\left(\frac{\pi}{\mathrm{3}}\right)\right)}{\mathrm{3}{cos}\left({h}\left(\frac{\pi}{\mathrm{3}}\right)\right)+{sin}\left({h}\left(\frac{\pi}{\mathrm{3}}\right)\right)}\right) \\ $$$$\:=\frac{\mathrm{4}\pi\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{3}+{tan}\left({h}\left(\frac{\pi}{\mathrm{3}}\right)\right)}\right)\:\checkmark \\ $$$$\:\:\:\:\:\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com