Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 124261 by Ar Brandon last updated on 02/Dec/20

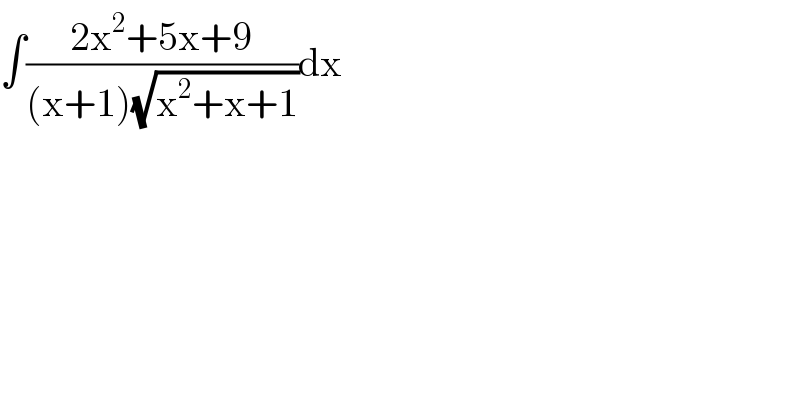
∫((2x^2 +5x+9)/((x+1)(√(x^2 +x+1))))dx

$$\int\frac{\mathrm{2x}^{\mathrm{2}} +\mathrm{5x}+\mathrm{9}}{\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}\mathrm{dx} \\ $$

Commented by MJS_new last updated on 02/Dec/20

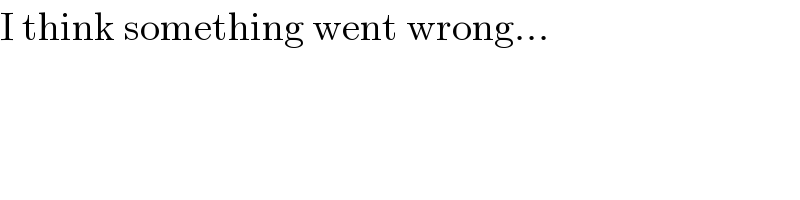
I think something went wrong...

$$\mathrm{I}\:\mathrm{think}\:\mathrm{something}\:\mathrm{went}\:\mathrm{wrong}... \\ $$

Commented by Ar Brandon last updated on 02/Dec/20

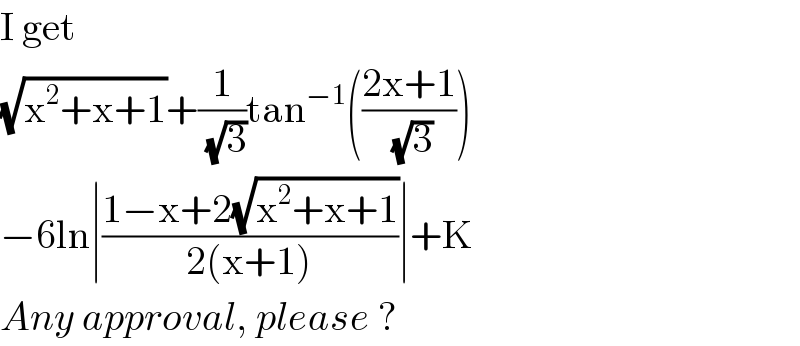
I get (√(x^2 +x+1))+(1/( (√3)))tan^(−1) (((2x+1)/( (√3)))) −6ln∣((1−x+2(√(x^2 +x+1)))/(2(x+1)))∣+K Any approval, please ?

$$\mathrm{I}\:\mathrm{get} \\ $$$$\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right) \\ $$$$−\mathrm{6ln}\mid\frac{\mathrm{1}−\mathrm{x}+\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}{\mathrm{2}\left(\mathrm{x}+\mathrm{1}\right)}\mid+\mathrm{K} \\ $$$${Any}\:{approval},\:{please}\:? \\ $$

Answered by MJS_new last updated on 02/Dec/20

∫((2x^2 +5x+9)/((x+1)(√(x^2 +x+1))))dx= [t=x+(1/2) → dx=dt] =4∫((2t^2 +3t+7)/((2t+1)(√(4t^2 +3))))dt= [u=(((√3)(2t+(√(4t^2 +3))))/3) → dt=((√(3(4t^2 +3)))/(2(2t+(√(4t^2 +3)))))] =∫((3(√3)u^4 +18u^3 +50(√3)u^2 −18u+3(√3))/(2u^2 (3u^2 +2(√3)u−3)))du= =∫(((√3)/2)−(6/(u+(√3)))+(2/u)+(6/(u−((√3)/3)))−((√3)/(2u^2 )))du= =((√3)/2)u−6ln (u+(√3))+2ln u +6ln (u−((√3)/3)) +((√3)/(2u))= =(((√3)(u^2 +1))/(2u))+6ln ((3u−(√3))/(u+(√3))) +2ln u = ... =2(√(x^2 +x+1))+6ln ((x−1+2(√(x^2 +x+1)))/(x+1)) +2ln (2x+1+2(√(x^2 +x+1))) +C

$$\int\frac{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{9}}{\left({x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}={x}+\frac{\mathrm{1}}{\mathrm{2}}\:\rightarrow\:{dx}={dt}\right] \\ $$$$=\mathrm{4}\int\frac{\mathrm{2}{t}^{\mathrm{2}} +\mathrm{3}{t}+\mathrm{7}}{\left(\mathrm{2}{t}+\mathrm{1}\right)\sqrt{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{3}}}{dt}= \\ $$$$\:\:\:\:\:\left[{u}=\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{t}+\sqrt{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{3}}\right)}{\mathrm{3}}\:\rightarrow\:{dt}=\frac{\sqrt{\mathrm{3}\left(\mathrm{4}{t}^{\mathrm{2}} +\mathrm{3}\right)}}{\mathrm{2}\left(\mathrm{2}{t}+\sqrt{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{3}}\right)}\right] \\ $$$$=\int\frac{\mathrm{3}\sqrt{\mathrm{3}}{u}^{\mathrm{4}} +\mathrm{18}{u}^{\mathrm{3}} +\mathrm{50}\sqrt{\mathrm{3}}{u}^{\mathrm{2}} −\mathrm{18}{u}+\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}{u}^{\mathrm{2}} \left(\mathrm{3}{u}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{3}}{u}−\mathrm{3}\right)}{du}= \\ $$$$=\int\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\mathrm{6}}{{u}+\sqrt{\mathrm{3}}}+\frac{\mathrm{2}}{{u}}+\frac{\mathrm{6}}{{u}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}{u}^{\mathrm{2}} }\right){du}= \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{u}−\mathrm{6ln}\:\left({u}+\sqrt{\mathrm{3}}\right)+\mathrm{2ln}\:{u}\:+\mathrm{6ln}\:\left({u}−\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\right)\:+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}{u}}= \\ $$$$=\frac{\sqrt{\mathrm{3}}\left({u}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{2}{u}}+\mathrm{6ln}\:\frac{\mathrm{3}{u}−\sqrt{\mathrm{3}}}{{u}+\sqrt{\mathrm{3}}}\:+\mathrm{2ln}\:{u}\:= \\ $$$$... \\ $$$$=\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}+\mathrm{6ln}\:\frac{{x}−\mathrm{1}+\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{{x}+\mathrm{1}}\:+\mathrm{2ln}\:\left(\mathrm{2}{x}+\mathrm{1}+\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\right)\:+{C} \\ $$

Commented by Ar Brandon last updated on 02/Dec/20

Thanks Sir, I found my mistake.

Commented by Ar Brandon last updated on 02/Dec/20

��Lol, OK ��

Commented by Ar Brandon last updated on 02/Dec/20

By the way. I left a message for you privately. Can you please check ?��

Commented by Ar Brandon last updated on 02/Dec/20

I don't think so, bro. Perhaps you're talking about the difference in sign. It's due to the absolute value of "u" I think.

Commented by Ar Brandon last updated on 02/Dec/20

OK. Thanks for your opinion, Sir. I'll check and post my solution.

Commented by Ar Brandon last updated on 02/Dec/20

Sir, I don't understand how you decide on your change of variables everytime. And they sound pretty fast��

Commented by MJS_new last updated on 02/Dec/20

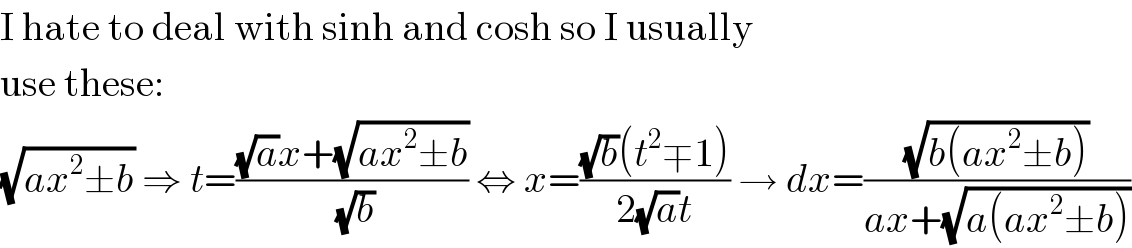
I hate to deal with sinh and cosh so I usually use these: (√(ax^2 ±b)) ⇒ t=(((√a)x+(√(ax^2 ±b)))/( (√b))) ⇔ x=(((√b)(t^2 ∓1))/(2(√a)t)) → dx=((√(b(ax^2 ±b)))/(ax+(√(a(ax^2 ±b)))))

$$\mathrm{I}\:\mathrm{hate}\:\mathrm{to}\:\mathrm{deal}\:\mathrm{with}\:\mathrm{sinh}\:\mathrm{and}\:\mathrm{cosh}\:\mathrm{so}\:\mathrm{I}\:\mathrm{usually} \\ $$$$\mathrm{use}\:\mathrm{these}: \\ $$$$\sqrt{{ax}^{\mathrm{2}} \pm{b}}\:\Rightarrow\:{t}=\frac{\sqrt{{a}}{x}+\sqrt{{ax}^{\mathrm{2}} \pm{b}}}{\:\sqrt{{b}}}\:\Leftrightarrow\:{x}=\frac{\sqrt{{b}}\left({t}^{\mathrm{2}} \mp\mathrm{1}\right)}{\mathrm{2}\sqrt{{a}}{t}}\:\rightarrow\:{dx}=\frac{\sqrt{{b}\left({ax}^{\mathrm{2}} \pm{b}\right)}}{{ax}+\sqrt{{a}\left({ax}^{\mathrm{2}} \pm{b}\right)}} \\ $$

Commented by Ar Brandon last updated on 02/Dec/20

Oh, I see ! ��

Commented by Dwaipayan Shikari last updated on 02/Dec/20

One or two more sir :)

$$\left.{One}\:{or}\:{two}\:{more}\:{sir}\::\right) \\ $$

Commented by Dwaipayan Shikari last updated on 02/Dec/20

I have told that sir may share one or more examples regarding this process ��

Commented by Ar Brandon last updated on 02/Dec/20

No, I meant on telegram. Sorry I didn't precise.

Answered by Ar Brandon last updated on 02/Dec/20

I=∫((2x^2 +5x+9)/((x+1)(√(x^2 +x+1))))dx ((2x^2 +5x+9)/(x+1))=((2(x+1)^2 +(x+1)+6)/(x+1))=2(x+1)+1+(6/(x+1)) I=∫{2(x+1)+1+(6/(x+1))}∙(dx/( (√(x^2 +x+1)))) =2∫((x+1)/( (√(x^2 +x+1))))dx+∫(dx/( (√(x^2 +x+1))))+6∫(dx/((x+1)(√(x^2 +x+1)))) =∫((2x+1)/( (√(x^2 +x+1))))dx+2∫(dx/( (√(x^2 +x+1))))+6∫(dx/((x+1)(√(x^2 +x+1)))) =2(√(x^2 +x+1))+2ln∣(x+(1/2))+(√(x^2 +x+1))∣+6J For J, Let (1/(x+1))=u ⇒ −(dx/((x+1)^2 ))=du ⇒ dx=−(du/u^2 ) ⇒ x=(1/u)−1, x^2 +x+1=(1/u^2 )−(1/u)+1 J=−∫(u/( (√((1/u^2 )−(1/u)+1))))∙(du/u^2 )=−∫(du/( (√(1−u+u^2 )))) =−∫(du/( (√((u−(1/2))^2 +(((√3)/2))^2 ))))=−sinh^(−1) (((u−1/2)/( (√3)/2)))+C =−ln∣(u−(1/2))+(√((u−(1/2))^2 +(((√3)/2))^2 ))∣+C =−ln∣((1/(x+1))−(1/2))+(√((1/((x+1)^2 ))−(1/(x+1))+1))∣+C =−ln∣((1−x+2(√(x^2 +x+1)))/(2(x+1)))∣+C ⇒I=2(√(x^2 +x+1))+2ln∣(x+(1/2))+(√(x^2 +x+1))∣−6ln∣((1−x+2(√(x^2 +x+1)))/(2(x+1)))∣+K

$$\mathcal{I}=\int\frac{\mathrm{2x}^{\mathrm{2}} +\mathrm{5x}+\mathrm{9}}{\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}\mathrm{dx}\: \\ $$$$\frac{\mathrm{2x}^{\mathrm{2}} +\mathrm{5x}+\mathrm{9}}{\mathrm{x}+\mathrm{1}}=\frac{\mathrm{2}\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{x}+\mathrm{1}\right)+\mathrm{6}}{\mathrm{x}+\mathrm{1}}=\mathrm{2}\left(\mathrm{x}+\mathrm{1}\right)+\mathrm{1}+\frac{\mathrm{6}}{\mathrm{x}+\mathrm{1}} \\ $$$$\mathcal{I}=\int\left\{\mathrm{2}\left(\mathrm{x}+\mathrm{1}\right)+\mathrm{1}+\frac{\mathrm{6}}{\mathrm{x}+\mathrm{1}}\right\}\centerdot\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}} \\ $$$$\:\:\:=\mathrm{2}\int\frac{\mathrm{x}+\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}\mathrm{dx}+\int\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}+\mathrm{6}\int\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}} \\ $$$$\:\:\:=\int\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}\mathrm{dx}+\mathrm{2}\int\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}+\mathrm{6}\int\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}} \\ $$$$\:\:\:=\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}+\mathrm{2ln}\mid\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\mid+\mathrm{6}\mathcal{J} \\ $$$$\mathrm{For}\:\mathcal{J}, \\ $$$$\mathrm{Let}\:\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}=\mathrm{u}\:\Rightarrow\:−\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{du}\:\Rightarrow\:\mathrm{dx}=−\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\mathrm{x}=\frac{\mathrm{1}}{\mathrm{u}}−\mathrm{1},\:\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}=\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{u}}+\mathrm{1} \\ $$$$\mathcal{J}=−\int\frac{\mathrm{u}}{\:\sqrt{\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{u}}+\mathrm{1}}}\centerdot\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} }=−\int\frac{\mathrm{du}}{\:\sqrt{\mathrm{1}−\mathrm{u}+\mathrm{u}^{\mathrm{2}} }} \\ $$$$\:\:\:\:=−\int\frac{\mathrm{du}}{\:\sqrt{\left(\mathrm{u}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }}=−\mathrm{sinh}^{−\mathrm{1}} \left(\frac{\mathrm{u}−\mathrm{1}/\mathrm{2}}{\:\sqrt{\mathrm{3}}/\mathrm{2}}\right)+\mathrm{C} \\ $$$$\:\:\:\:=−\mathrm{ln}\mid\left(\mathrm{u}−\frac{\mathrm{1}}{\mathrm{2}}\right)+\sqrt{\left(\mathrm{u}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }\mid+\mathrm{C} \\ $$$$\:\:\:\:=−\mathrm{ln}\mid\left(\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\right)+\sqrt{\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}+\mathrm{1}}\mid+\mathrm{C} \\ $$$$\:\:\:\:=−\mathrm{ln}\mid\frac{\mathrm{1}−\mathrm{x}+\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}{\mathrm{2}\left(\mathrm{x}+\mathrm{1}\right)}\mid+\mathrm{C} \\ $$$$\Rightarrow\mathcal{I}=\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}+\mathrm{2ln}\mid\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\mid−\mathrm{6ln}\mid\frac{\mathrm{1}−\mathrm{x}+\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}{\mathrm{2}\left(\mathrm{x}+\mathrm{1}\right)}\mid+\mathrm{K} \\ $$

Answered by Dwaipayan Shikari last updated on 02/Dec/20

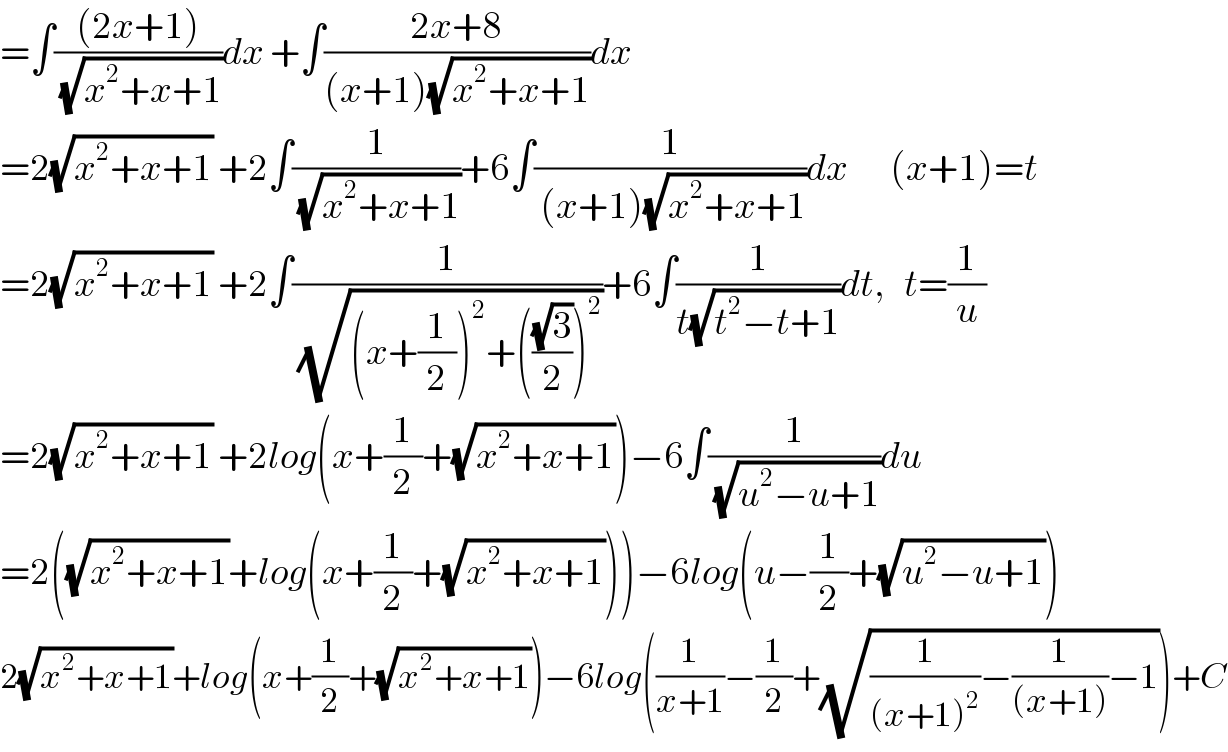
=∫(((2x+1))/( (√(x^2 +x+1))))dx +∫((2x+8)/((x+1)(√(x^2 +x+1))))dx =2(√(x^2 +x+1)) +2∫(1/( (√(x^2 +x+1))))+6∫(1/( (x+1)(√(x^2 +x+1))))dx (x+1)=t =2(√(x^2 +x+1)) +2∫(1/( (√((x+(1/2))^2 +(((√3)/2))^2 ))))+6∫(1/(t(√(t^2 −t+1))))dt, t=(1/u) =2(√(x^2 +x+1)) +2log(x+(1/2)+(√(x^2 +x+1)))−6∫(1/( (√(u^2 −u+1))))du =2((√(x^2 +x+1))+log(x+(1/2)+(√(x^2 +x+1))))−6log(u−(1/2)+(√(u^2 −u+1))) 2(√(x^2 +x+1))+log(x+(1/2)+(√(x^2 +x+1)))−6log((1/(x+1))−(1/2)+(√((1/((x+1)^2 ))−(1/((x+1)))−1)))+C

$$=\int\frac{\left(\mathrm{2}{x}+\mathrm{1}\right)}{\:\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{dx}\:+\int\frac{\mathrm{2}{x}+\mathrm{8}}{\left({x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{dx} \\ $$$$=\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:+\mathrm{2}\int\frac{\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}+\mathrm{6}\int\frac{\mathrm{1}}{\:\left({x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{dx}\:\:\:\:\:\:\:\left({x}+\mathrm{1}\right)={t} \\ $$$$=\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:+\mathrm{2}\int\frac{\mathrm{1}}{\:\sqrt{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }}+\mathrm{6}\int\frac{\mathrm{1}}{{t}\sqrt{{t}^{\mathrm{2}} −{t}+\mathrm{1}}}{dt},\:\:\:{t}=\frac{\mathrm{1}}{{u}} \\ $$$$=\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:+\mathrm{2}{log}\left({x}+\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\right)−\mathrm{6}\int\frac{\mathrm{1}}{\:\sqrt{{u}^{\mathrm{2}} −{u}+\mathrm{1}}}{du} \\ $$$$=\mathrm{2}\left(\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}+{log}\left({x}+\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\right)\right)−\mathrm{6}{log}\left({u}−\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{{u}^{\mathrm{2}} −{u}+\mathrm{1}}\right) \\ $$$$\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}+{log}\left({x}+\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\right)−\mathrm{6}{log}\left(\frac{\mathrm{1}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)}−\mathrm{1}}\right)+{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com