
Question Number 124627 by ajfour last updated on 04/Dec/20
Commented by ajfour last updated on 04/Dec/20
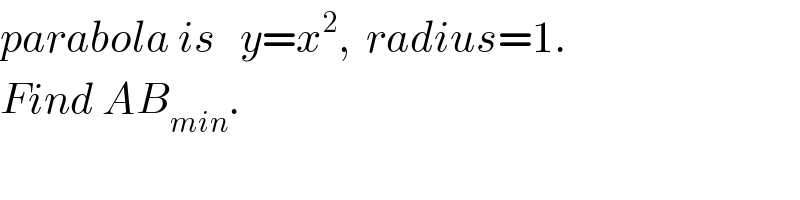
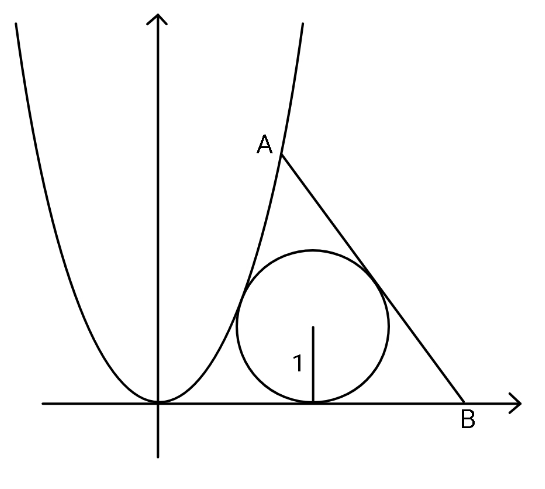
$${parabola}\:{is}\:\:\:{y}={x}^{\mathrm{2}} ,\:\:{radius}=\mathrm{1}. \\ $$$${Find}\:{AB}_{{min}} . \\ $$
Answered by mr W last updated on 05/Dec/20
Commented by mr W last updated on 05/Dec/20
Commented by mr W last updated on 05/Dec/20
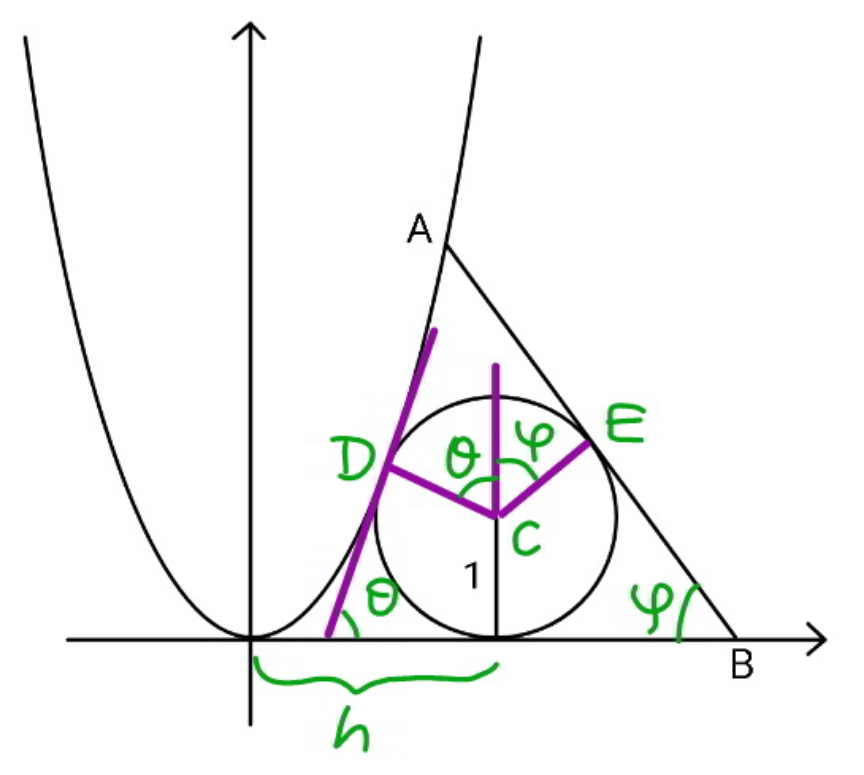
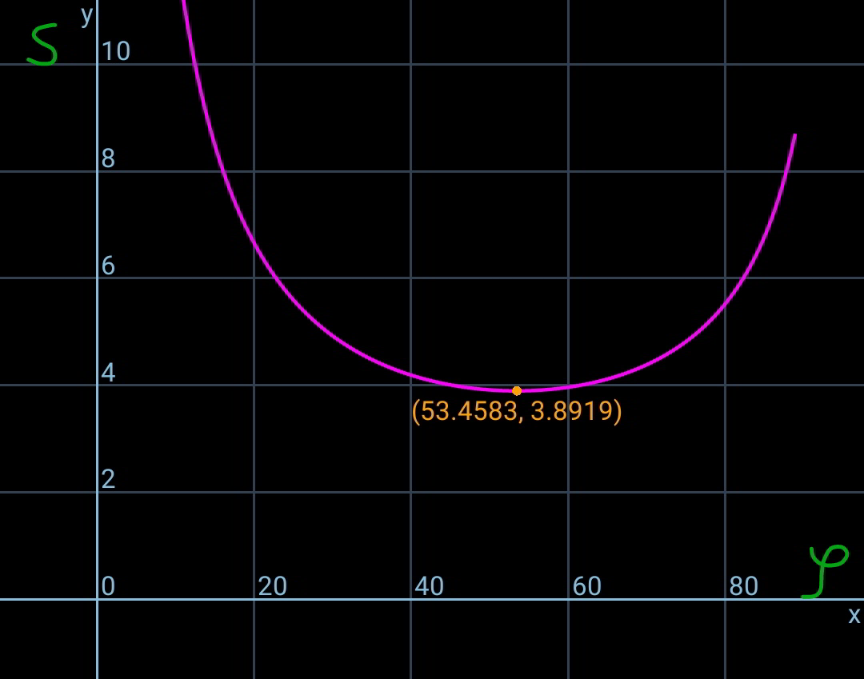
![C(h,1) x_D =h−sin θ y_D =1+cos θ 1+cos θ=(h−sin θ)^2 ...(i) tan θ=2(h−sin θ) ...(ii) ⇒4(1+cos θ)=tan^2 θ=(1/(cos^2 θ))−1 ⇒(1/(cos^3 θ))−(5/(cos θ))−4=0 ⇒((1/(cos θ))+1)((1/(cos^2 θ))−(1/(cos θ))−4)=0 ⇒(1/(cos θ))=((1+(√(17)))/2)=(8/( (√(17))−1)) ⇒θ=cos^(−1) (((√(17))−1)/8)≈67.021343° ⇒h=sin θ+((tan θ)/2)≈2.099798 x_E =h+sin ϕ y_E =1+cos ϕ eqn. of AB: y=1+cos ϕ−tan ϕ (x−h−sin ϕ) 0=1+cos ϕ−tan ϕ (x_B −h−sin ϕ) ⇒x_B =h+sin ϕ+((1+cos ϕ)/(tan ϕ)) x_A ^2 =1+cos ϕ−tan ϕ (x_A −h−sin ϕ) x_A ^2 +tan ϕ x_A −[1+cos ϕ+tan ϕ (h+sin ϕ)]=0 ⇒x_A =(1/2)(−tan ϕ+(√(tan^2 ϕ+4[1+cos ϕ+tan ϕ (h+sin ϕ)])) s=AB=((x_B −x_A )/(cos ϕ)) s=(1/(cos ϕ)){h+sin ϕ+((1+cos ϕ)/(tan ϕ))+((tan ϕ)/2)−(√(((tan^2 ϕ)/4)+1+cos ϕ+tan ϕ (h+sin ϕ)))} ⇒s_(min) ≈3.8919 at ϕ=53.4583°](Q124656.png)
$${C}\left({h},\mathrm{1}\right) \\ $$$${x}_{{D}} ={h}−\mathrm{sin}\:\theta \\ $$$${y}_{{D}} =\mathrm{1}+\mathrm{cos}\:\theta \\ $$$$\mathrm{1}+\mathrm{cos}\:\theta=\left({h}−\mathrm{sin}\:\theta\right)^{\mathrm{2}} \:\:\:...\left({i}\right) \\ $$$$\mathrm{tan}\:\theta=\mathrm{2}\left({h}−\mathrm{sin}\:\theta\right)\:\:\:...\left({ii}\right) \\ $$$$\Rightarrow\mathrm{4}\left(\mathrm{1}+\mathrm{cos}\:\theta\right)=\mathrm{tan}^{\mathrm{2}} \:\theta=\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:\theta}−\mathrm{1} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{3}} \:\theta}−\frac{\mathrm{5}}{\mathrm{cos}\:\theta}−\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow\left(\frac{\mathrm{1}}{\mathrm{cos}\:\theta}+\mathrm{1}\right)\left(\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:\theta}−\frac{\mathrm{1}}{\mathrm{cos}\:\theta}−\mathrm{4}\right)=\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{cos}\:\theta}=\frac{\mathrm{1}+\sqrt{\mathrm{17}}}{\mathrm{2}}=\frac{\mathrm{8}}{\:\sqrt{\mathrm{17}}−\mathrm{1}} \\ $$$$\Rightarrow\theta=\mathrm{cos}^{−\mathrm{1}} \frac{\sqrt{\mathrm{17}}−\mathrm{1}}{\mathrm{8}}\approx\mathrm{67}.\mathrm{021343}° \\ $$$$\Rightarrow{h}=\mathrm{sin}\:\theta+\frac{\mathrm{tan}\:\theta}{\mathrm{2}}\approx\mathrm{2}.\mathrm{099798} \\ $$$$ \\ $$$${x}_{{E}} ={h}+\mathrm{sin}\:\varphi \\ $$$${y}_{{E}} =\mathrm{1}+\mathrm{cos}\:\varphi \\ $$$${eqn}.\:{of}\:{AB}: \\ $$$${y}=\mathrm{1}+\mathrm{cos}\:\varphi−\mathrm{tan}\:\varphi\:\left({x}−{h}−\mathrm{sin}\:\varphi\right) \\ $$$$ \\ $$$$\mathrm{0}=\mathrm{1}+\mathrm{cos}\:\varphi−\mathrm{tan}\:\varphi\:\left({x}_{{B}} −{h}−\mathrm{sin}\:\varphi\right) \\ $$$$\Rightarrow{x}_{{B}} ={h}+\mathrm{sin}\:\varphi+\frac{\mathrm{1}+\mathrm{cos}\:\varphi}{\mathrm{tan}\:\varphi} \\ $$$${x}_{{A}} ^{\mathrm{2}} =\mathrm{1}+\mathrm{cos}\:\varphi−\mathrm{tan}\:\varphi\:\left({x}_{{A}} −{h}−\mathrm{sin}\:\varphi\right) \\ $$$${x}_{{A}} ^{\mathrm{2}} +\mathrm{tan}\:\varphi\:{x}_{{A}} −\left[\mathrm{1}+\mathrm{cos}\:\varphi+\mathrm{tan}\:\varphi\:\left({h}+\mathrm{sin}\:\varphi\right)\right]=\mathrm{0} \\ $$$$\Rightarrow{x}_{{A}} =\frac{\mathrm{1}}{\mathrm{2}}\left(−\mathrm{tan}\:\varphi+\sqrt{\mathrm{tan}^{\mathrm{2}} \:\varphi+\mathrm{4}\left[\mathrm{1}+\mathrm{cos}\:\varphi+\mathrm{tan}\:\varphi\:\left({h}+\mathrm{sin}\:\varphi\right)\right]}\right. \\ $$$${s}={AB}=\frac{{x}_{{B}} −{x}_{{A}} }{\mathrm{cos}\:\varphi} \\ $$$${s}=\frac{\mathrm{1}}{\mathrm{cos}\:\varphi}\left\{{h}+\mathrm{sin}\:\varphi+\frac{\mathrm{1}+\mathrm{cos}\:\varphi}{\mathrm{tan}\:\varphi}+\frac{\mathrm{tan}\:\varphi}{\mathrm{2}}−\sqrt{\frac{\mathrm{tan}^{\mathrm{2}} \:\varphi}{\mathrm{4}}+\mathrm{1}+\mathrm{cos}\:\varphi+\mathrm{tan}\:\varphi\:\left({h}+\mathrm{sin}\:\varphi\right)}\right\} \\ $$$$\Rightarrow{s}_{{min}} \approx\mathrm{3}.\mathrm{8919}\:{at}\:\varphi=\mathrm{53}.\mathrm{4583}° \\ $$
Commented by mr W last updated on 05/Dec/20

Commented by ajfour last updated on 05/Dec/20
$${Understood}\:{your}\:{solution},\:{Sir}! \\ $$$${Thanks}\:{a}\:{lot}. \\ $$
