Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 125204 by bemath last updated on 09/Dec/20

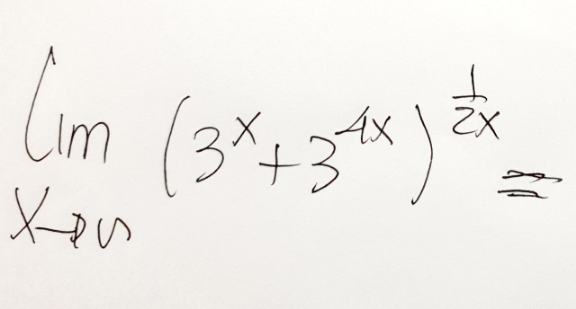
Answered by liberty last updated on 09/Dec/20

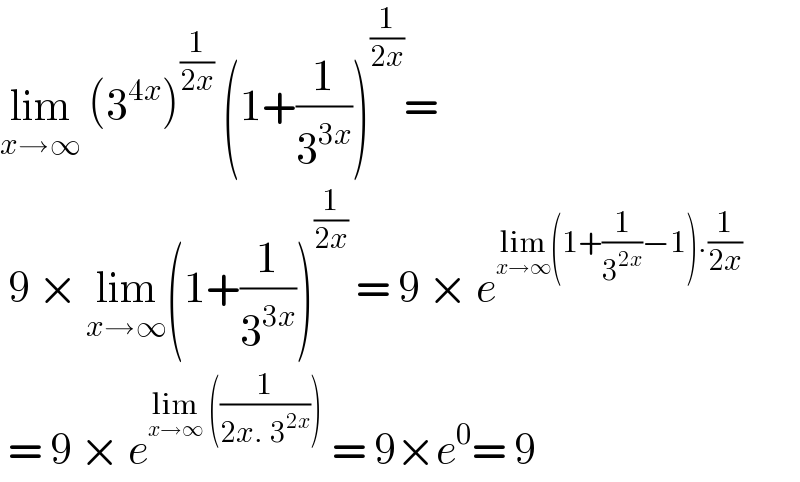
lim_(x→∞) (3^(4x) )^(1/(2x)) (1+(1/3^(3x) ))^(1/(2x)) = 9 × lim_(x→∞) (1+(1/3^(3x) ))^(1/(2x)) = 9 × e^(lim_(x→∞) (1+(1/3^(2x) )−1).(1/(2x))) = 9 × e^(lim_(x→∞) ((1/(2x. 3^(2x) )))) = 9×e^0 = 9

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{3}^{\mathrm{4}{x}} \right)^{\frac{\mathrm{1}}{\mathrm{2}{x}}} \:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}{x}} }\right)^{\frac{\mathrm{1}}{\mathrm{2}{x}}} =\: \\ $$$$\:\mathrm{9}\:×\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}{x}} }\right)^{\frac{\mathrm{1}}{\mathrm{2}{x}}} \:=\:\mathrm{9}\:×\:{e}^{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}{x}} }−\mathrm{1}\right).\frac{\mathrm{1}}{\mathrm{2}{x}}} \\ $$$$\:=\:\mathrm{9}\:×\:{e}^{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{\mathrm{2}{x}.\:\mathrm{3}^{\mathrm{2}{x}} }\right)} \:=\:\mathrm{9}×{e}^{\mathrm{0}} =\:\mathrm{9} \\ $$

Answered by Dwaipayan Shikari last updated on 09/Dec/20

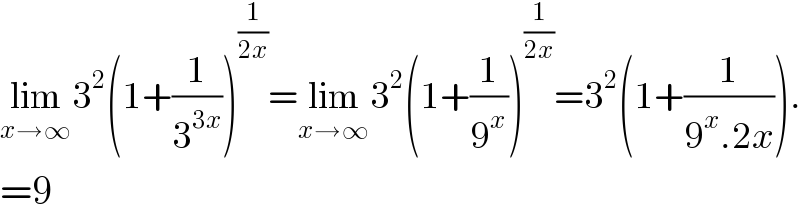
lim_(x→∞) 3^2 (1+(1/3^(3x) ))^(1/(2x)) =lim_(x→∞) 3^2 (1+(1/9^x ))^(1/(2x)) =3^2 (1+(1/(9^x .2x))). =9

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}3}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}{x}} }\right)^{\frac{\mathrm{1}}{\mathrm{2}{x}}} =\underset{{x}\rightarrow\infty} {\mathrm{lim}3}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{9}^{{x}} }\right)^{\frac{\mathrm{1}}{\mathrm{2}{x}}} =\mathrm{3}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{9}^{{x}} .\mathrm{2}{x}}\right). \\ $$$$=\mathrm{9} \\ $$

Answered by mathmax by abdo last updated on 09/Dec/20

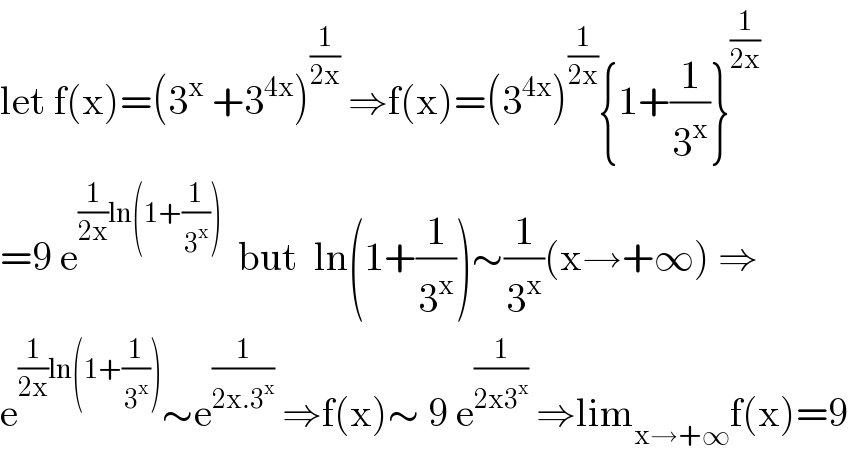
let f(x)=(3^x +3^(4x) )^(1/(2x)) ⇒f(x)=(3^(4x) )^(1/(2x)) {1+(1/3^x )}^(1/(2x)) =9 e^((1/(2x))ln(1+(1/3^x ))) but ln(1+(1/3^x ))∼(1/3^x )(x→+∞) ⇒ e^((1/(2x))ln(1+(1/3^x ))) ∼e^(1/(2x.3^x )) ⇒f(x)∼ 9 e^(1/(2x3^x )) ⇒lim_(x→+∞) f(x)=9

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{3}^{\mathrm{x}} \:+\mathrm{3}^{\mathrm{4x}} \right)^{\frac{\mathrm{1}}{\mathrm{2x}}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{3}^{\mathrm{4x}} \right)^{\frac{\mathrm{1}}{\mathrm{2x}}} \left\{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{x}} }\right\}^{\frac{\mathrm{1}}{\mathrm{2x}}} \\ $$$$=\mathrm{9}\:\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2x}}\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{x}} }\right)} \:\:\mathrm{but}\:\:\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{x}} }\right)\sim\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{x}} }\left(\mathrm{x}\rightarrow+\infty\right)\:\Rightarrow \\ $$$$\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2x}}\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{x}} }\right)} \sim\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2x}.\mathrm{3}^{\mathrm{x}} }} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\sim\:\mathrm{9}\:\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2x3}^{\mathrm{x}} }} \:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{f}\left(\mathrm{x}\right)=\mathrm{9} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com