
Question Number 125907 by ajfour last updated on 15/Dec/20
Commented by ajfour last updated on 15/Dec/20
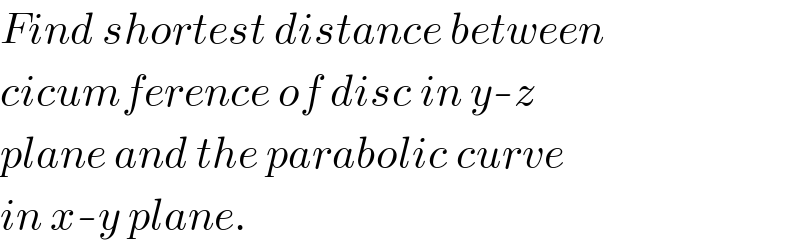
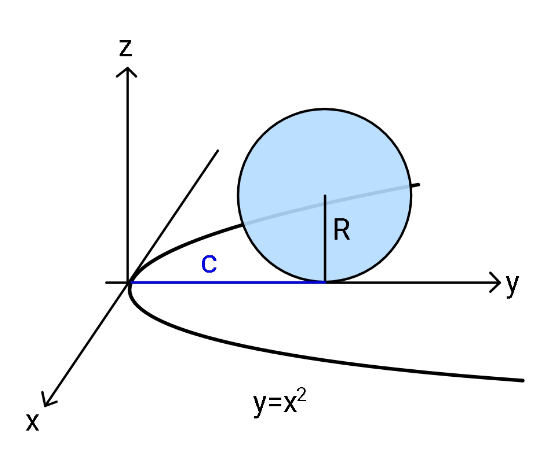
$${Find}\:{shortest}\:{distance}\:{between} \\ $$$${cicumference}\:{of}\:{disc}\:{in}\:{y}-{z} \\ $$$${plane}\:{and}\:{the}\:{parabolic}\:{curve} \\ $$$${in}\:{x}-{y}\:{plane}. \\ $$
Answered by ajfour last updated on 15/Dec/20
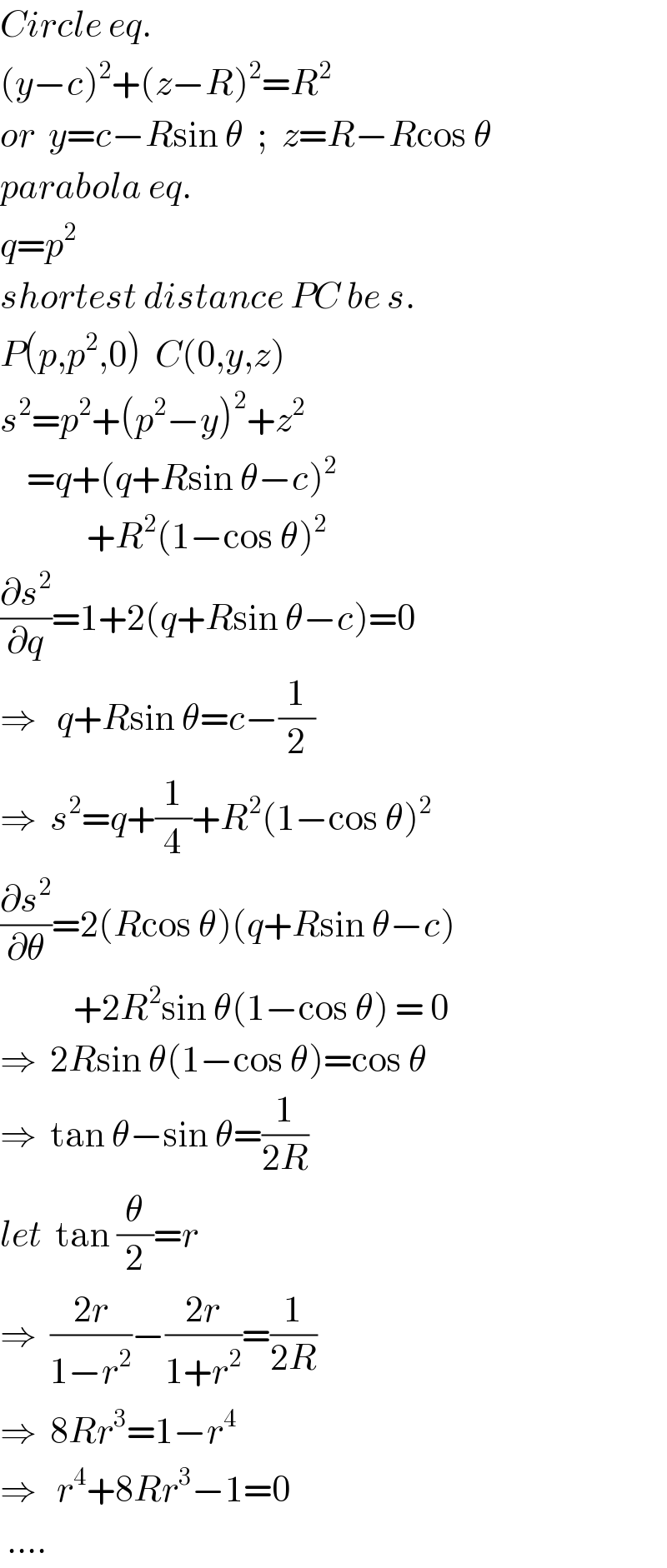
$${Circle}\:{eq}. \\ $$$$\left({y}−{c}\right)^{\mathrm{2}} +\left({z}−{R}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$${or}\:\:{y}={c}−{R}\mathrm{sin}\:\theta\:\:;\:\:{z}={R}−{R}\mathrm{cos}\:\theta \\ $$$${parabola}\:{eq}. \\ $$$${q}={p}^{\mathrm{2}} \\ $$$${shortest}\:{distance}\:{PC}\:{be}\:{s}. \\ $$$${P}\left({p},{p}^{\mathrm{2}} ,\mathrm{0}\right)\:\:{C}\left(\mathrm{0},{y},{z}\right) \\ $$$${s}^{\mathrm{2}} ={p}^{\mathrm{2}} +\left({p}^{\mathrm{2}} −{y}\right)^{\mathrm{2}} +{z}^{\mathrm{2}} \\ $$$$\:\:\:\:={q}+\left({q}+{R}\mathrm{sin}\:\theta−{c}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:+{R}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} \\ $$$$\frac{\partial{s}^{\mathrm{2}} }{\partial{q}}=\mathrm{1}+\mathrm{2}\left({q}+{R}\mathrm{sin}\:\theta−{c}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\:{q}+{R}\mathrm{sin}\:\theta={c}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:{s}^{\mathrm{2}} ={q}+\frac{\mathrm{1}}{\mathrm{4}}+{R}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} \\ $$$$\frac{\partial{s}^{\mathrm{2}} }{\partial\theta}=\mathrm{2}\left({R}\mathrm{cos}\:\theta\right)\left({q}+{R}\mathrm{sin}\:\theta−{c}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:+\mathrm{2}{R}^{\mathrm{2}} \mathrm{sin}\:\theta\left(\mathrm{1}−\mathrm{cos}\:\theta\right)\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{2}{R}\mathrm{sin}\:\theta\left(\mathrm{1}−\mathrm{cos}\:\theta\right)=\mathrm{cos}\:\theta \\ $$$$\Rightarrow\:\:\mathrm{tan}\:\theta−\mathrm{sin}\:\theta=\frac{\mathrm{1}}{\mathrm{2}{R}} \\ $$$${let}\:\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}={r} \\ $$$$\Rightarrow\:\:\frac{\mathrm{2}{r}}{\mathrm{1}−{r}^{\mathrm{2}} }−\frac{\mathrm{2}{r}}{\mathrm{1}+{r}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}{R}} \\ $$$$\Rightarrow\:\:\mathrm{8}{Rr}^{\mathrm{3}} =\mathrm{1}−{r}^{\mathrm{4}} \\ $$$$\Rightarrow\:\:\:{r}^{\mathrm{4}} +\mathrm{8}{Rr}^{\mathrm{3}} −\mathrm{1}=\mathrm{0} \\ $$$$\:....\:\: \\ $$
Answered by mr W last updated on 15/Dec/20
Commented by mr W last updated on 15/Dec/20

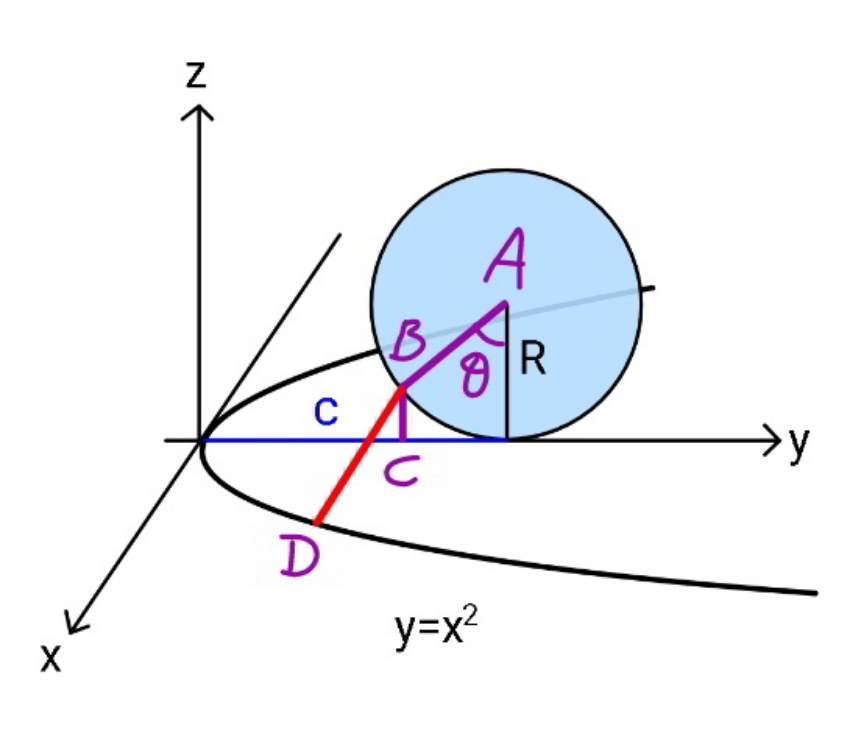
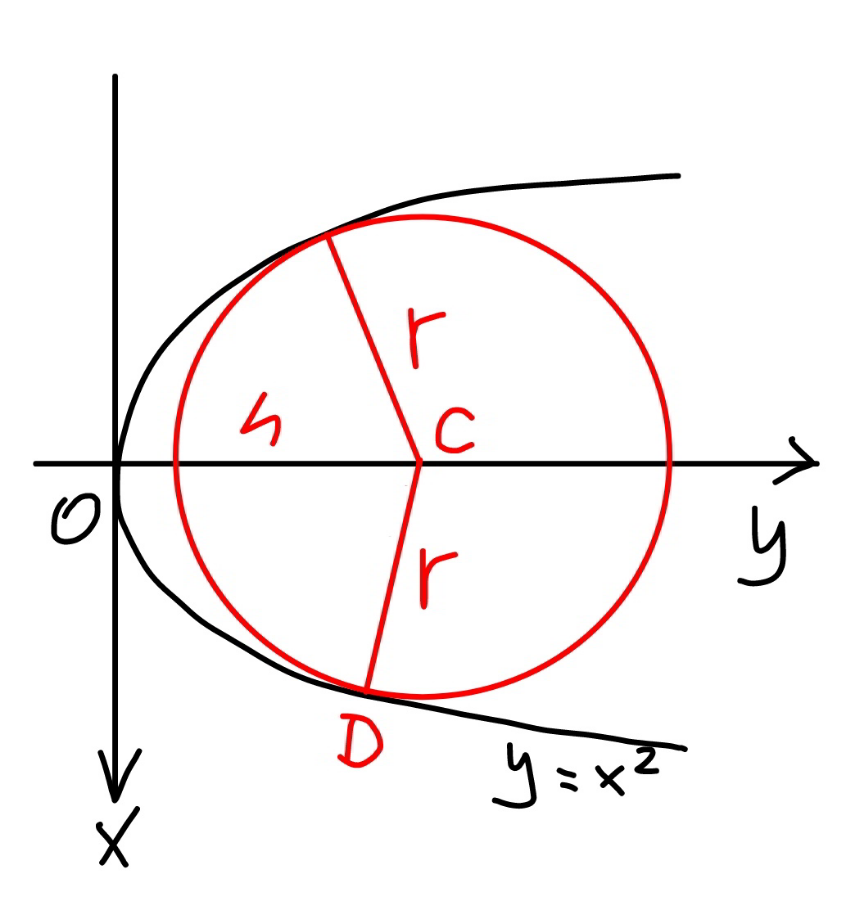
$${let}'{s}\:{say}\:{the}\:{point}\:{B}\:{has}\:{the}\:{shortest} \\ $$$${distance}\:{to}\:{the}\:{parabola}\:{at}\:{point}\:{D}. \\ $$$${let}\:{BD}={s} \\ $$$${such}\:{that}\:{d}\:{is}\:{minimum},\:{the}\:{sphere} \\ $$$${with}\:{center}\:{at}\:{B}\:{and}\:{radius}\:{d}\:{must} \\ $$$${tangent}\:{the}\:{parabola}\:{at}\:{D}. \\ $$$${let}\:{CD}={r} \\ $$$${the}\:{circle}\:{with}\:{center}\:{at}\:{C}\:{and}\:{radius} \\ $$$${r}\:{must}\:{tangent}\:{the}\:{parabola}\:{at}\:{D}. \\ $$$${let}\:{OC}={h}={c}−{R}\:\mathrm{sin}\:\theta \\ $$
Commented by mr W last updated on 15/Dec/20
Commented by mr W last updated on 15/Dec/20
![y=x^2 x^2 +(y−h)^2 =r^2 y^2 −(2h−1)y+h^2 −r^2 =0 for tangency: Δ=(2h−1)^2 −4(h^2 −r^2 )=0 −4h+1+4r^2 =0 ⇒r^2 =((4h−1)/4) h=c−R sin θ s^2 =r^2 +R^2 (1−cos θ)^2 s^2 =c−(1/4)+R[R(1−cos θ)^2 −sin θ] ((d(s^2 ))/dθ)=0 ⇒2R(1−cos θ)sin θ−cos θ=0 ⇒tan θ−sin θ=(1/(2R)) with t=tan (θ/2) ⇒((2t)/(1−t^2 ))−((2t)/(1+t^2 ))=(1/(2R)) ⇒t^4 +8Rt^3 −1=0 ...](Q125941.png)
$${y}={x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +\left({y}−{h}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${y}^{\mathrm{2}} −\left(\mathrm{2}{h}−\mathrm{1}\right){y}+{h}^{\mathrm{2}} −{r}^{\mathrm{2}} =\mathrm{0} \\ $$$${for}\:{tangency}: \\ $$$$\Delta=\left(\mathrm{2}{h}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}\left({h}^{\mathrm{2}} −{r}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$−\mathrm{4}{h}+\mathrm{1}+\mathrm{4}{r}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{r}^{\mathrm{2}} =\frac{\mathrm{4}{h}−\mathrm{1}}{\mathrm{4}} \\ $$$${h}={c}−{R}\:\mathrm{sin}\:\theta \\ $$$${s}^{\mathrm{2}} ={r}^{\mathrm{2}} +{R}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} \\ $$$${s}^{\mathrm{2}} ={c}−\frac{\mathrm{1}}{\mathrm{4}}+{R}\left[{R}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} −\mathrm{sin}\:\theta\right] \\ $$$$\frac{{d}\left({s}^{\mathrm{2}} \right)}{{d}\theta}=\mathrm{0}\:\Rightarrow\mathrm{2}{R}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)\mathrm{sin}\:\theta−\mathrm{cos}\:\theta=\mathrm{0} \\ $$$$\Rightarrow\mathrm{tan}\:\theta−\mathrm{sin}\:\theta=\frac{\mathrm{1}}{\mathrm{2}{R}} \\ $$$${with}\:{t}=\mathrm{tan}\:\frac{\theta}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }−\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}{R}} \\ $$$$\Rightarrow{t}^{\mathrm{4}} +\mathrm{8}{Rt}^{\mathrm{3}} −\mathrm{1}=\mathrm{0} \\ $$$$... \\ $$
Commented by ajfour last updated on 15/Dec/20
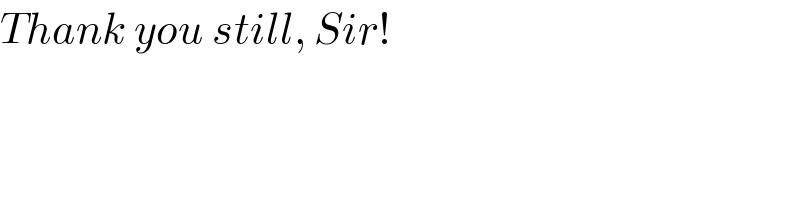
$${Thank}\:{you}\:{still},\:{Sir}! \\ $$
