
Question Number 127017 by mnjuly1970 last updated on 26/Dec/20
![...NICE CALCULUS... prove that :: ∫_0 ^( ∞) (((x^2 ln(πx))/π^(πx) ))dx =(1/((πln(π))^3 ))[(3−2(γ+ln(ln(π)))]](Q127017.png)
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:...{NICE}\:\:\:\:\:{CALCULUS}... \\ $$$$\:\:{prove}\:{that}\::: \\ $$$$\int_{\mathrm{0}} ^{\:\infty} \:\left(\frac{{x}^{\mathrm{2}} {ln}\left(\pi{x}\right)}{\pi^{\pi{x}} }\right){dx} \\ $$$$\:\:=\frac{\mathrm{1}}{\left(\pi{ln}\left(\pi\right)\right)^{\mathrm{3}} }\left[\left(\mathrm{3}−\mathrm{2}\left(\gamma+{ln}\left({ln}\left(\pi\right)\right)\right)\right]\right. \\ $$
Answered by mindispower last updated on 26/Dec/20
![=∫_0 ^∞ x^2 ln(πx)e^(−πxln(π)) dx u=πln(π)x ⇒dx=(du/(πln(π))) ⇔∫_0 ^∞ (u^2 /(π^2 ln^2 (π)))ln((u/(ln(π))))e^(−u) .(du/(πln(π))) =(1/(π^3 ln^3 (π)))[∫_0 ^∞ u^2 ln(u)e^(−u) du−ln(lnπ)∫_0 ^∞ u^2 e^(−u) ] =(1/(π^3 ln^3 (π))){Γ′(3)−ln(ln(π).Γ(3)} =((Γ(3).Ψ(3))/(π^3 ln^3 (π)))−(1/(π^3 ln^3 (π)))2ln(lnπ) =2((1/2)+1−γ).(1/(π^3 ln^3 (π)))−((2ln(lnπ))/(π^3 ln^3 (π))) =((3−2γ)/(π^3 ln^3 (π)))−((2ln(lnπ))/(π^3 ln^3 (π)))=(1/((πlnπ)^3 ))[(3−2(γ+ln(lnπ))]](Q127019.png)
$$=\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{2}} {ln}\left(\pi{x}\right){e}^{−\pi{xln}\left(\pi\right)} {dx} \\ $$$${u}=\pi{ln}\left(\pi\right){x} \\ $$$$\Rightarrow{dx}=\frac{{du}}{\pi{ln}\left(\pi\right)} \\ $$$$\Leftrightarrow\int_{\mathrm{0}} ^{\infty} \frac{{u}^{\mathrm{2}} }{\pi^{\mathrm{2}} {ln}^{\mathrm{2}} \left(\pi\right)}{ln}\left(\frac{{u}}{{ln}\left(\pi\right)}\right){e}^{−{u}} .\frac{{du}}{\pi{ln}\left(\pi\right)} \\ $$$$=\frac{\mathrm{1}}{\pi^{\mathrm{3}} {ln}^{\mathrm{3}} \left(\pi\right)}\left[\int_{\mathrm{0}} ^{\infty} {u}^{\mathrm{2}} {ln}\left({u}\right){e}^{−{u}} {du}−{ln}\left({ln}\pi\right)\int_{\mathrm{0}} ^{\infty} {u}^{\mathrm{2}} {e}^{−{u}} \right] \\ $$$$=\frac{\mathrm{1}}{\pi^{\mathrm{3}} {ln}^{\mathrm{3}} \left(\pi\right)}\left\{\Gamma'\left(\mathrm{3}\right)−{ln}\left({ln}\left(\pi\right).\Gamma\left(\mathrm{3}\right)\right\}\right. \\ $$$$=\frac{\Gamma\left(\mathrm{3}\right).\Psi\left(\mathrm{3}\right)}{\pi^{\mathrm{3}} {ln}^{\mathrm{3}} \left(\pi\right)}−\frac{\mathrm{1}}{\pi^{\mathrm{3}} {ln}^{\mathrm{3}} \left(\pi\right)}\mathrm{2}{ln}\left({ln}\pi\right) \\ $$$$=\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1}−\gamma\right).\frac{\mathrm{1}}{\pi^{\mathrm{3}} {ln}^{\mathrm{3}} \left(\pi\right)}−\frac{\mathrm{2}{ln}\left({ln}\pi\right)}{\pi^{\mathrm{3}} {ln}^{\mathrm{3}} \left(\pi\right)} \\ $$$$=\frac{\mathrm{3}−\mathrm{2}\gamma}{\pi^{\mathrm{3}} {ln}^{\mathrm{3}} \left(\pi\right)}−\frac{\mathrm{2}{ln}\left({ln}\pi\right)}{\pi^{\mathrm{3}} {ln}^{\mathrm{3}} \left(\pi\right)}=\frac{\mathrm{1}}{\left(\pi{ln}\pi\right)^{\mathrm{3}} }\left[\left(\mathrm{3}−\mathrm{2}\left(\gamma+{ln}\left({ln}\pi\right)\right)\right]\right. \\ $$
Commented by mnjuly1970 last updated on 26/Dec/20
$${peace}\:{be}\:{upon}\:{you} \\ $$$$\:\:{sir}\:{power}\:..{mercey}.. \\ $$
Answered by Dwaipayan Shikari last updated on 26/Dec/20
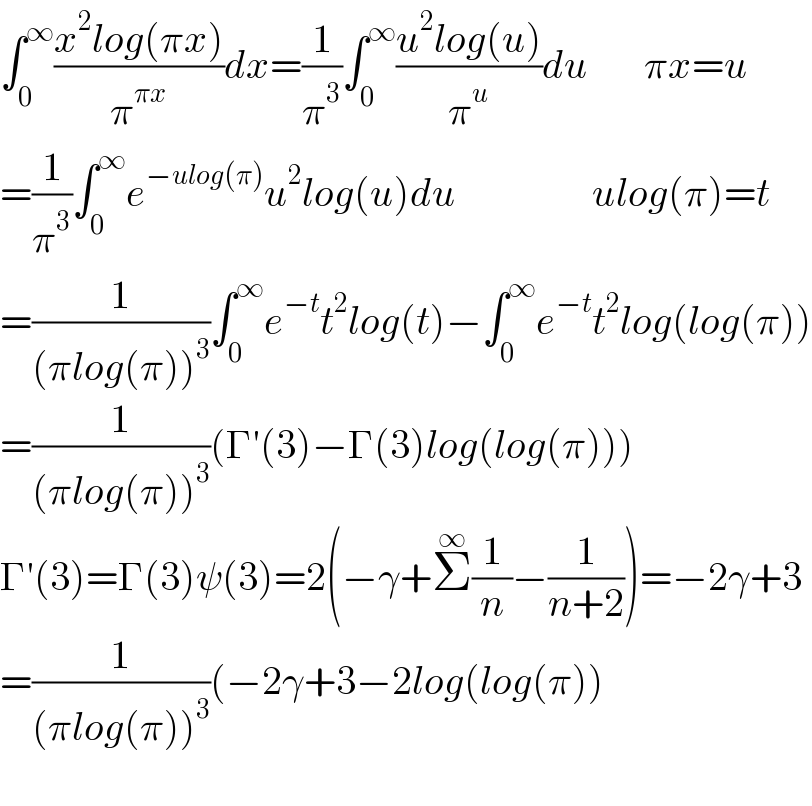
$$\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{2}} {log}\left(\pi{x}\right)}{\pi^{\pi{x}} }{dx}=\frac{\mathrm{1}}{\pi^{\mathrm{3}} }\int_{\mathrm{0}} ^{\infty} \frac{{u}^{\mathrm{2}} {log}\left({u}\right)}{\pi^{{u}} }{du}\:\:\:\:\:\:\:\pi{x}={u} \\ $$$$=\frac{\mathrm{1}}{\pi^{\mathrm{3}} }\int_{\mathrm{0}} ^{\infty} {e}^{−{ulog}\left(\pi\right)} {u}^{\mathrm{2}} {log}\left({u}\right){du}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{ulog}\left(\pi\right)={t} \\ $$$$=\frac{\mathrm{1}}{\left(\pi{log}\left(\pi\right)\right)^{\mathrm{3}} }\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} {t}^{\mathrm{2}} {log}\left({t}\right)−\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} {t}^{\mathrm{2}} {log}\left({log}\left(\pi\right)\right) \\ $$$$=\frac{\mathrm{1}}{\left(\pi{log}\left(\pi\right)\right)^{\mathrm{3}} }\left(\Gamma'\left(\mathrm{3}\right)−\Gamma\left(\mathrm{3}\right){log}\left({log}\left(\pi\right)\right)\right) \\ $$$$\Gamma'\left(\mathrm{3}\right)=\Gamma\left(\mathrm{3}\right)\psi\left(\mathrm{3}\right)=\mathrm{2}\left(−\gamma+\overset{\infty} {\sum}\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}\right)=−\mathrm{2}\gamma+\mathrm{3} \\ $$$$=\frac{\mathrm{1}}{\left(\pi{log}\left(\pi\right)\right)^{\mathrm{3}} }\left(−\mathrm{2}\gamma+\mathrm{3}−\mathrm{2}{log}\left({log}\left(\pi\right)\right)\right. \\ $$$$ \\ $$
