Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 127111 by benjo_mathlover last updated on 26/Dec/20

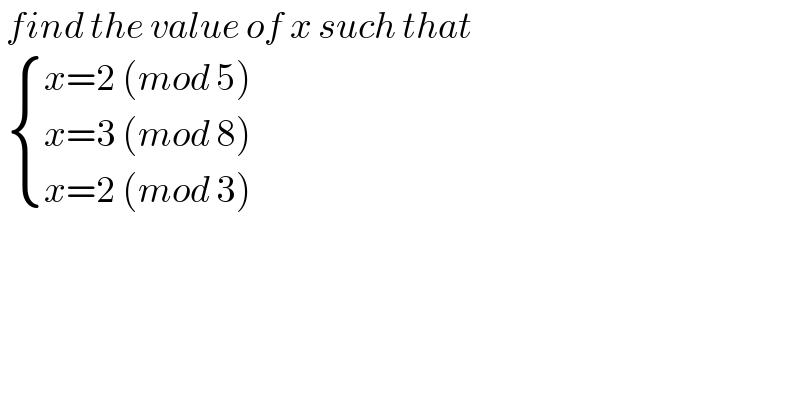
find the value of x such that { ((x=2 (mod 5))),((x=3 (mod 8) )),((x=2 (mod 3))) :}

$$\:{find}\:{the}\:{value}\:{of}\:{x}\:{such}\:{that}\: \\ $$$$\:\begin{cases}{{x}=\mathrm{2}\:\left({mod}\:\mathrm{5}\right)}\\{{x}=\mathrm{3}\:\left({mod}\:\mathrm{8}\right)\:}\\{{x}=\mathrm{2}\:\left({mod}\:\mathrm{3}\right)}\end{cases} \\ $$

Answered by liberty last updated on 04/Jan/21

given { ((x=2 (mod 5)...(i))),((x=3 (mod 8)...(ii))),((x=2 (mod 3)...(iii))) :} for(i) ⇒ 24a ≡ 2 (mod 5) −a≡2 (mod 5); a ≡−2 (mod 5) for(ii)⇒15b ≡ 3 (mod 8) −b ≡ 3 (mod 8) ; b ≡−3 (mod 8) for(iii)⇒40c ≡ 2 (mod 3) c ≡ 2 (mod 3) now we have the general solution ∴ 24(−2)+15(−3)+40(2)+120k ; k∈Z i.e : 120k−13 ; k∈Z or 120k +107 ; k∈Z

$${given}\:\begin{cases}{{x}=\mathrm{2}\:\left({mod}\:\mathrm{5}\right)...\left({i}\right)}\\{{x}=\mathrm{3}\:\left({mod}\:\mathrm{8}\right)...\left({ii}\right)}\\{{x}=\mathrm{2}\:\left({mod}\:\mathrm{3}\right)...\left({iii}\right)}\end{cases} \\ $$$${for}\left({i}\right)\:\Rightarrow\:\mathrm{24}{a}\:\equiv\:\mathrm{2}\:\left({mod}\:\mathrm{5}\right)\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−{a}\equiv\mathrm{2}\:\left({mod}\:\mathrm{5}\right);\:{a}\:\equiv−\mathrm{2}\:\left({mod}\:\mathrm{5}\right) \\ $$$${for}\left({ii}\right)\Rightarrow\mathrm{15}{b}\:\equiv\:\mathrm{3}\:\left({mod}\:\mathrm{8}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−{b}\:\equiv\:\mathrm{3}\:\left({mod}\:\mathrm{8}\right)\:;\:{b}\:\equiv−\mathrm{3}\:\left({mod}\:\mathrm{8}\right) \\ $$$${for}\left({iii}\right)\Rightarrow\mathrm{40}{c}\:\equiv\:\mathrm{2}\:\left({mod}\:\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{c}\:\equiv\:\mathrm{2}\:\left({mod}\:\mathrm{3}\right) \\ $$$${now}\:{we}\:{have}\:{the}\:{general}\:{solution}\: \\ $$$$\therefore\:\mathrm{24}\left(−\mathrm{2}\right)+\mathrm{15}\left(−\mathrm{3}\right)+\mathrm{40}\left(\mathrm{2}\right)+\mathrm{120}{k}\:;\:{k}\in\mathbb{Z} \\ $$$${i}.{e}\::\:\mathrm{120}{k}−\mathrm{13}\:;\:{k}\in\mathbb{Z}\:\mathrm{or}\:\mathrm{120}{k}\:+\mathrm{107}\:;\:{k}\in\mathbb{Z} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\: \\ $$

Answered by physicstutes last updated on 27/Dec/20

x ≡ 2 (mod 3) .....(i) ⇒ x = 3t + 2 , t ∈ Z......(i) x ≡ 3 (mod 8)......(ii) (i) in (i) ⇒ 3t + 2 ≡ 3 (mod 8) 3t ≡ −1 (mod 8) but −1 ≡ 7 (mod 8) therefore 3t ≡ 7 (mod 8) by trial and error we find a number t which when multiplied by 3 and divided by 8 gives a remainder of 7. so i find t = 3 after some tries. ⇒ t ≡ 3 (mod 8) ⇒ t = 8s + 3 , s ∈ Z......(iii) putting (iii) in (i) ⇒ x = 3(8s + 3) +2 = 24s +11 so : x = 24 s + 11 .....(iv) x ≡ 2 (mod 5)......(v) (iv) in (v) ⇒ 24s +11 ≡ 2 (mod 5) 24 s ≡ −9 (mod 5) but −9 ≡ 1 (mod 5) therefore 24s ≡ 1 (mod 5) by trial and error s ≡ 4 (mod 5) ⇒ s = 5u + 4 .....(vii) u ∈ Z ⇒ x = 24(5u + 4) + 11 x = 120 u +107 x ≡ 107 (mod 120)

$${x}\:\equiv\:\mathrm{2}\:\left(\mathrm{mod}\:\mathrm{3}\right)\:.....\left({i}\right)\:\Rightarrow\:{x}\:=\:\mathrm{3}{t}\:+\:\mathrm{2}\:,\:{t}\:\in\:\mathbb{Z}......\left({i}\right) \\ $$$$\:{x}\:\equiv\:\mathrm{3}\:\left(\mathrm{mod}\:\mathrm{8}\right)......\left({ii}\right) \\ $$$$\left({i}\right)\:\mathrm{in}\:\left({i}\right)\:\Rightarrow\:\mathrm{3}{t}\:+\:\mathrm{2}\:\equiv\:\mathrm{3}\:\left(\mathrm{mod}\:\mathrm{8}\right) \\ $$$$\:\mathrm{3}{t}\:\equiv\:−\mathrm{1}\:\left(\mathrm{mod}\:\mathrm{8}\right) \\ $$$$\mathrm{but}\:−\mathrm{1}\:\equiv\:\mathrm{7}\:\left(\mathrm{mod}\:\mathrm{8}\right)\:\:\mathrm{therefore}\: \\ $$$$\:\mathrm{3}{t}\:\equiv\:\mathrm{7}\:\left(\mathrm{mod}\:\mathrm{8}\right)\:\mathrm{by}\:\mathrm{trial}\:\mathrm{and}\:\mathrm{error}\:\mathrm{we}\:\mathrm{find}\:\mathrm{a}\:\mathrm{number}\:{t}\:\mathrm{which}\:\mathrm{when} \\ $$$$\mathrm{multiplied}\:\mathrm{by}\:\mathrm{3}\:\mathrm{and}\:\mathrm{divided}\:\mathrm{by}\:\mathrm{8}\:\mathrm{gives}\:\mathrm{a}\:\mathrm{remainder}\:\mathrm{of}\:\mathrm{7}. \\ $$$$\:\mathrm{so}\:\mathrm{i}\:\mathrm{find}\:{t}\:=\:\mathrm{3}\:\mathrm{after}\:\mathrm{some}\:\mathrm{tries}. \\ $$$$\Rightarrow\:{t}\:\equiv\:\mathrm{3}\:\left(\mathrm{mod}\:\mathrm{8}\right)\:\Rightarrow\:{t}\:=\:\mathrm{8}{s}\:+\:\mathrm{3}\:,\:{s}\:\in\:\mathbb{Z}......\left({iii}\right) \\ $$$$\mathrm{putting}\:\left({iii}\right)\:\mathrm{in}\:\left({i}\right)\:\Rightarrow\:{x}\:=\:\mathrm{3}\left(\mathrm{8}{s}\:+\:\mathrm{3}\right)\:+\mathrm{2}\:=\:\mathrm{24}{s}\:+\mathrm{11} \\ $$$$\:\mathrm{so}\::\:\:\:\:{x}\:=\:\mathrm{24}\:{s}\:+\:\mathrm{11}\:.....\left({iv}\right)\: \\ $$$$\:{x}\:\equiv\:\mathrm{2}\:\left(\mathrm{mod}\:\mathrm{5}\right)......\left({v}\right) \\ $$$$\left({iv}\right)\:\mathrm{in}\:\left({v}\right)\:\Rightarrow\:\:\:\mathrm{24}{s}\:+\mathrm{11}\:\equiv\:\mathrm{2}\:\left(\mathrm{mod}\:\mathrm{5}\right)\: \\ $$$$\mathrm{24}\:{s}\:\equiv\:−\mathrm{9}\:\left(\mathrm{mod}\:\mathrm{5}\right)\: \\ $$$$\mathrm{but}\:−\mathrm{9}\:\equiv\:\mathrm{1}\:\left(\mathrm{mod}\:\mathrm{5}\right)\:\mathrm{therefore}\:\:\mathrm{24}{s}\:\equiv\:\mathrm{1}\:\left(\mathrm{mod}\:\mathrm{5}\right)\:\mathrm{by}\:\mathrm{trial}\:\mathrm{and}\:\mathrm{error} \\ $$$$\:{s}\:\equiv\:\mathrm{4}\:\left(\mathrm{mod}\:\mathrm{5}\right)\:\Rightarrow\:{s}\:=\:\mathrm{5}{u}\:+\:\mathrm{4}\:.....\left({vii}\right)\:{u}\:\in\:\mathbb{Z} \\ $$$$\Rightarrow\:{x}\:=\:\mathrm{24}\left(\mathrm{5}{u}\:+\:\mathrm{4}\right)\:+\:\mathrm{11} \\ $$$$\:\:\:\:\:{x}\:=\:\mathrm{120}\:{u}\:+\mathrm{107} \\ $$$${x}\:\equiv\:\mathrm{107}\:\left(\mathrm{mod}\:\mathrm{120}\right)\: \\ $$

Answered by floor(10²Eta[1]) last updated on 27/Dec/20

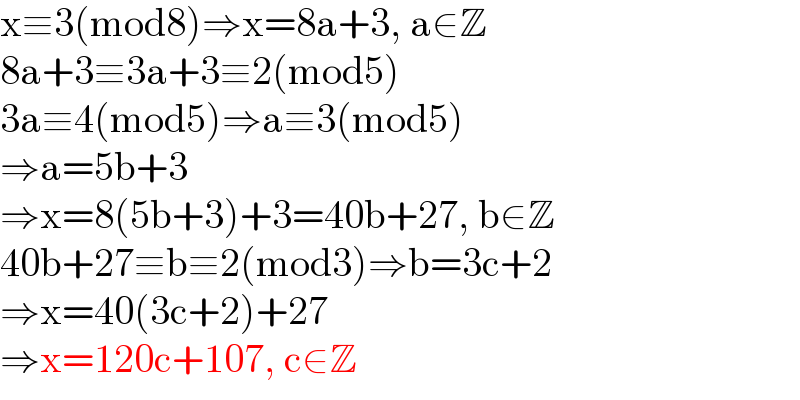
x≡3(mod8)⇒x=8a+3, a∈Z 8a+3≡3a+3≡2(mod5) 3a≡4(mod5)⇒a≡3(mod5) ⇒a=5b+3 ⇒x=8(5b+3)+3=40b+27, b∈Z 40b+27≡b≡2(mod3)⇒b=3c+2 ⇒x=40(3c+2)+27 ⇒x=120c+107, c∈Z

$$\mathrm{x}\equiv\mathrm{3}\left(\mathrm{mod8}\right)\Rightarrow\mathrm{x}=\mathrm{8a}+\mathrm{3},\:\mathrm{a}\in\mathbb{Z} \\ $$$$\mathrm{8a}+\mathrm{3}\equiv\mathrm{3a}+\mathrm{3}\equiv\mathrm{2}\left(\mathrm{mod5}\right) \\ $$$$\mathrm{3a}\equiv\mathrm{4}\left(\mathrm{mod5}\right)\Rightarrow\mathrm{a}\equiv\mathrm{3}\left(\mathrm{mod5}\right) \\ $$$$\Rightarrow\mathrm{a}=\mathrm{5b}+\mathrm{3} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{8}\left(\mathrm{5b}+\mathrm{3}\right)+\mathrm{3}=\mathrm{40b}+\mathrm{27},\:\mathrm{b}\in\mathbb{Z} \\ $$$$\mathrm{40b}+\mathrm{27}\equiv\mathrm{b}\equiv\mathrm{2}\left(\mathrm{mod3}\right)\Rightarrow\mathrm{b}=\mathrm{3c}+\mathrm{2} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{40}\left(\mathrm{3c}+\mathrm{2}\right)+\mathrm{27} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{120c}+\mathrm{107},\:\mathrm{c}\in\mathbb{Z} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com