
Question Number 127446 by mnjuly1970 last updated on 29/Dec/20
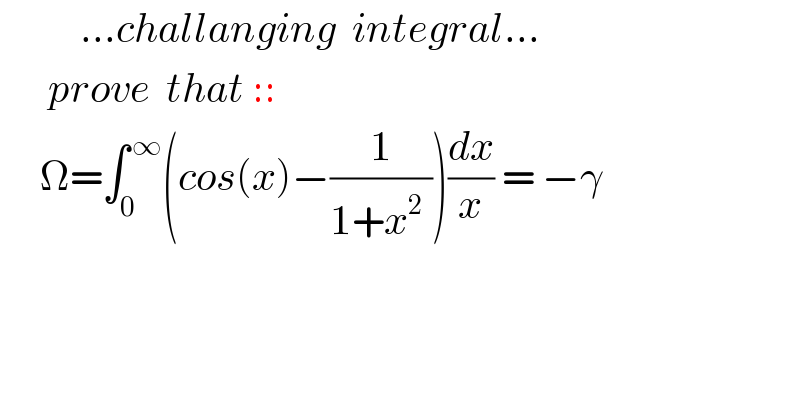
$$\:\:\:\:\:\:\:\:\:\:...{challanging}\:\:{integral}... \\ $$$$\:\:\:\:\:\:{prove}\:\:{that}\::: \\ $$$$\:\:\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\infty} \left({cos}\left({x}\right)−\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} \:}\right)\frac{{dx}}{{x}}\:=\:−\gamma\:\: \\ $$$$ \\ $$
Answered by mindispower last updated on 31/Dec/20
![Ci(x)=−∫_x ^∞ ((cos(t))/t)dt=γ+ln(x)−∫_0 ^x ((1−cos(t))/t)dt Ω=lim_(t→0) ∫_t ^∞ (cos(x)−(1/(1+x^2 ))).(dx/x) =lim_(t→0) (−γ−ln(t)+∫_0 ^t ((1−cos(x))/x)dx−∫_t ^∞ (dx/(x(1+x^2 )))) =lim_(t→0) (−γ−ln(t)+∫_0 ^t ((1−cos(x))/x)dx−B) B=∫_t ^∞ (1/(x(1+x^2 )))=((1+x^2 −x.x)/(x(1+x^2 )))=∫_t ^∞ (1/x)−(x/(1+x^2 ))dx =[ln(x)−((ln(1+x^2 ))/2)]_t ^∞ =−ln(t)+((ln(1+t^2 ))/2) Ω=lim_(t→0) (−γ−ln(t)+∫_0 ^t ((1−cos(x))/x)dx+ln(t)−((ln(1+t^2 ))/2)) Ω=lim_(t→0) (−γ+∫_0 ^t ((1−cos(x))/x)dx) lim_(t→0) ∫_0 ^t ((1−cos(x))/x)dx=0 ((1−cos(x))/x)=g(x) 0≤((1−cos(x))/x) _(x∈[0,t]) =Σ_(k≥1) (((−1)^(k+1) )/((2k!)))x^(2k−1) ≤(x/2) ⇒0≤∫_0 ^t ((1−cos(x))/x)dx≤(t^2 /4)→0 Ω=lim_(t→0) (−γ+∫_0 ^t ((1−cos(x))/x)dx)=−γ+0=−γ Ω=−γ](Q127602.png)
$${Ci}\left({x}\right)=−\int_{{x}} ^{\infty} \frac{{cos}\left({t}\right)}{{t}}{dt}=\gamma+{ln}\left({x}\right)−\int_{\mathrm{0}} ^{{x}} \frac{\mathrm{1}−{cos}\left({t}\right)}{{t}}{dt}\: \\ $$$$\Omega=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\int_{{t}} ^{\infty} \left({cos}\left({x}\right)−\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\right).\frac{{dx}}{{x}} \\ $$$$=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(−\gamma−{ln}\left({t}\right)+\int_{\mathrm{0}} ^{{t}} \frac{\mathrm{1}−{cos}\left({x}\right)}{{x}}{dx}−\int_{{t}} ^{\infty} \frac{{dx}}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\right) \\ $$$$=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(−\gamma−{ln}\left({t}\right)+\int_{\mathrm{0}} ^{{t}} \frac{\mathrm{1}−{cos}\left({x}\right)}{{x}}{dx}−{B}\right) \\ $$$${B}=\int_{{t}} ^{\infty} \frac{\mathrm{1}}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}=\frac{\mathrm{1}+{x}^{\mathrm{2}} −{x}.{x}}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}=\int_{{t}} ^{\infty} \frac{\mathrm{1}}{{x}}−\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$=\left[{ln}\left({x}\right)−\frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\mathrm{2}}\right]_{{t}} ^{\infty} =−{ln}\left({t}\right)+\frac{{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\mathrm{2}} \\ $$$$\Omega=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(−\gamma−{ln}\left({t}\right)+\int_{\mathrm{0}} ^{{t}} \frac{\mathrm{1}−{cos}\left({x}\right)}{{x}}{dx}+{ln}\left({t}\right)−\frac{{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\mathrm{2}}\right) \\ $$$$\Omega=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(−\gamma+\int_{\mathrm{0}} ^{{t}} \frac{\mathrm{1}−{cos}\left({x}\right)}{{x}}{dx}\right) \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\int_{\mathrm{0}} ^{{t}} \frac{\mathrm{1}−{cos}\left({x}\right)}{{x}}{dx}=\mathrm{0} \\ $$$$\frac{\mathrm{1}−{cos}\left({x}\right)}{{x}}={g}\left({x}\right) \\ $$$$\mathrm{0}\leqslant\frac{\mathrm{1}−{cos}\left({x}\right)}{{x}}\:\underset{{x}\in\left[\mathrm{0},{t}\right]} {\:}=\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} }{\left(\mathrm{2}{k}!\right)}{x}^{\mathrm{2}{k}−\mathrm{1}} \leqslant\frac{{x}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{0}\leqslant\int_{\mathrm{0}} ^{{t}} \frac{\mathrm{1}−{cos}\left({x}\right)}{{x}}{dx}\leqslant\frac{{t}^{\mathrm{2}} }{\mathrm{4}}\rightarrow\mathrm{0} \\ $$$$\Omega=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(−\gamma+\int_{\mathrm{0}} ^{{t}} \frac{\mathrm{1}−{cos}\left({x}\right)}{{x}}{dx}\right)=−\gamma+\mathrm{0}=−\gamma \\ $$$$\Omega=−\gamma \\ $$$$ \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 31/Dec/20
$${very}\:{nice}\:.{thanks}\:{alot}.. \\ $$$$ \\ $$
Commented by mindispower last updated on 31/Dec/20
$${pleasur}\:{sir}\:{happy}\:{new}\:{years}\:{all}\:{good}\:{things}\:{for} \\ $$$${you} \\ $$
