
Question Number 128922 by mnjuly1970 last updated on 11/Jan/21
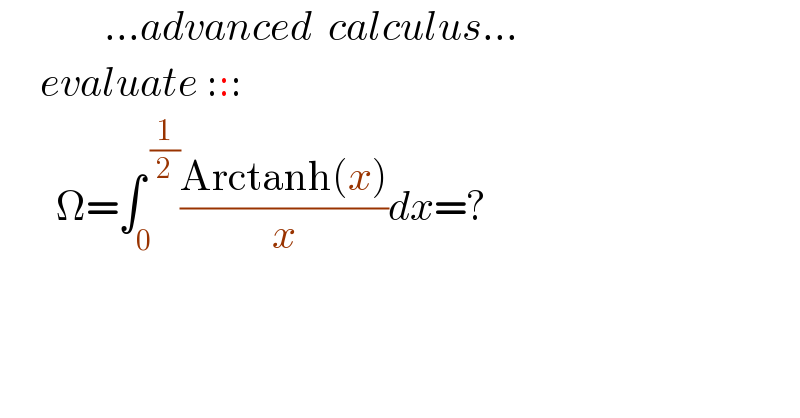
$$\:\:\:\:\:\:\:\:\:\:\:\:\:...{advanced}\:\:{calculus}... \\ $$$$\:\:\:\:\:{evaluate}\::::\: \\ $$$$\:\:\:\:\:\:\:\Omega=\int_{\mathrm{0}\:} ^{\:\frac{\mathrm{1}}{\mathrm{2}}} \frac{\mathrm{Arctanh}\left({x}\right)}{{x}}{dx}=? \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 11/Jan/21
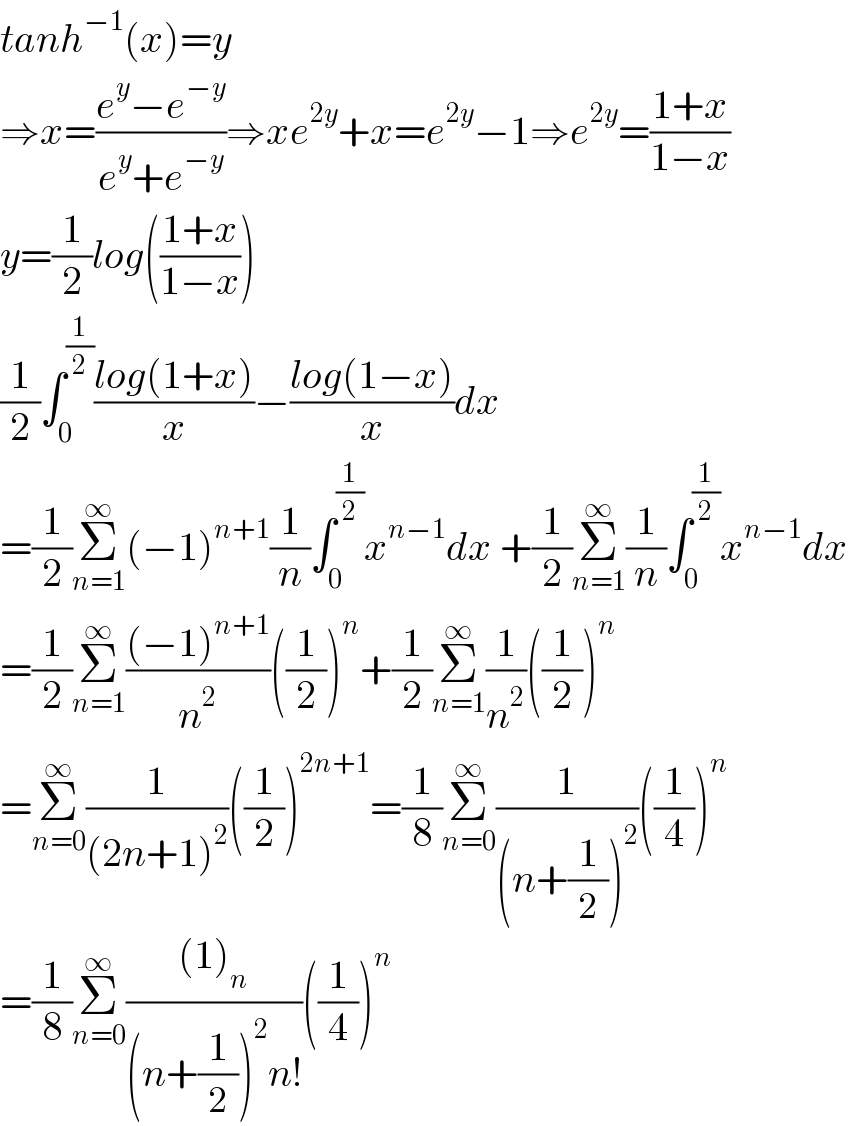
$${tanh}^{−\mathrm{1}} \left({x}\right)={y} \\ $$$$\Rightarrow{x}=\frac{{e}^{{y}} −{e}^{−{y}} }{{e}^{{y}} +{e}^{−{y}} }\Rightarrow{xe}^{\mathrm{2}{y}} +{x}={e}^{\mathrm{2}{y}} −\mathrm{1}\Rightarrow{e}^{\mathrm{2}{y}} =\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}} \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{{log}\left(\mathrm{1}+{x}\right)}{{x}}−\frac{{log}\left(\mathrm{1}−{x}\right)}{{x}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} {x}^{{n}−\mathrm{1}} {dx}\:+\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} {x}^{{n}−\mathrm{1}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}^{\mathrm{2}} }\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} +\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{8}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{{n}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{1}\right)_{{n}} }{\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} {n}!}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{{n}} \:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by Dwaipayan Shikari last updated on 11/Jan/21
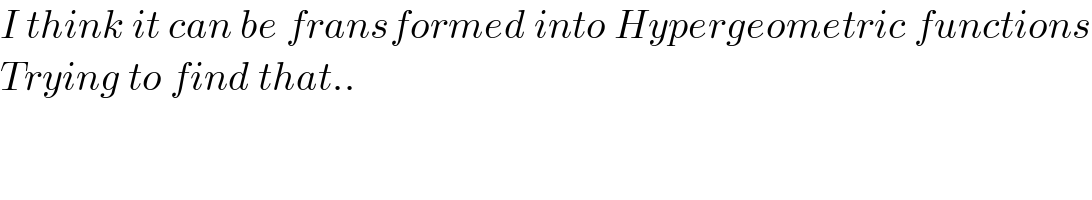
$${I}\:{think}\:{it}\:{can}\:{be}\:{fransformed}\:{into}\:{Hypergeometric}\:{functions} \\ $$$${Trying}\:{to}\:{find}\:{that}.. \\ $$
Commented by mnjuly1970 last updated on 11/Jan/21

$${thank}\:{you}\:{so}\:{much}.. \\ $$$$\:\:{li}_{\mathrm{2}} \left({x}\right)\:=−\int_{\mathrm{0}} ^{\:{x}} \frac{{ln}\left(\mathrm{1}−{t}\right)}{{t}}{dt} \\ $$$$\:\:\:{li}_{\mathrm{2}} \left({x}\right)+{li}_{\mathrm{2}} \left(\mathrm{1}−{x}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:−{ln}\left({x}\right){ln}\left(\mathrm{1}−{x}\right) \\ $$$$\:\:{of}\:{course}\:{you}\:{know} \\ $$$$\:\:{these}\:{better}\:{than}\:{that}\:{me}. \\ $$$$\:\:{i}\:{just}\:{mentioned}\:{it}...\left({dilogarithm}\:{function}\:{properties}\right).. \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 11/Jan/21
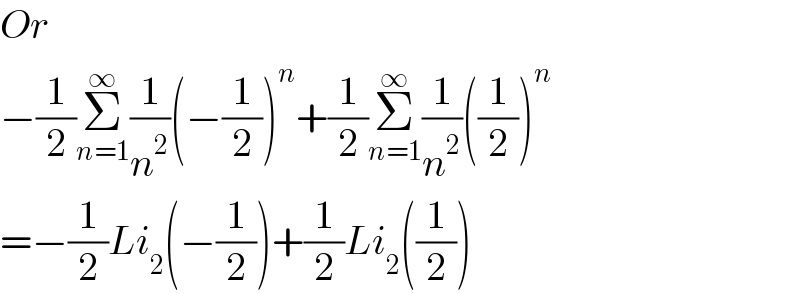
$${Or}\: \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} +\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}{Li}_{\mathrm{2}} \left(−\frac{\mathrm{1}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}{Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$
Commented by mnjuly1970 last updated on 11/Jan/21
$${very}\:{nice}\: \\ $$$${thank}\:{you}\:{mr}\:{dwaipayan} \\ $$
