
Question Number 129300 by Adel last updated on 14/Jan/21

$$ \\ $$ Find the polynomial divided by (x-2) the remaining 5 divided by (x-3) the remaining 9 and if divided by (x-4) the remaining 13 if divided by (x-10) 37 and if divided by (x-3/4) the remainder remains zero\\n
Answered by Olaf last updated on 14/Jan/21
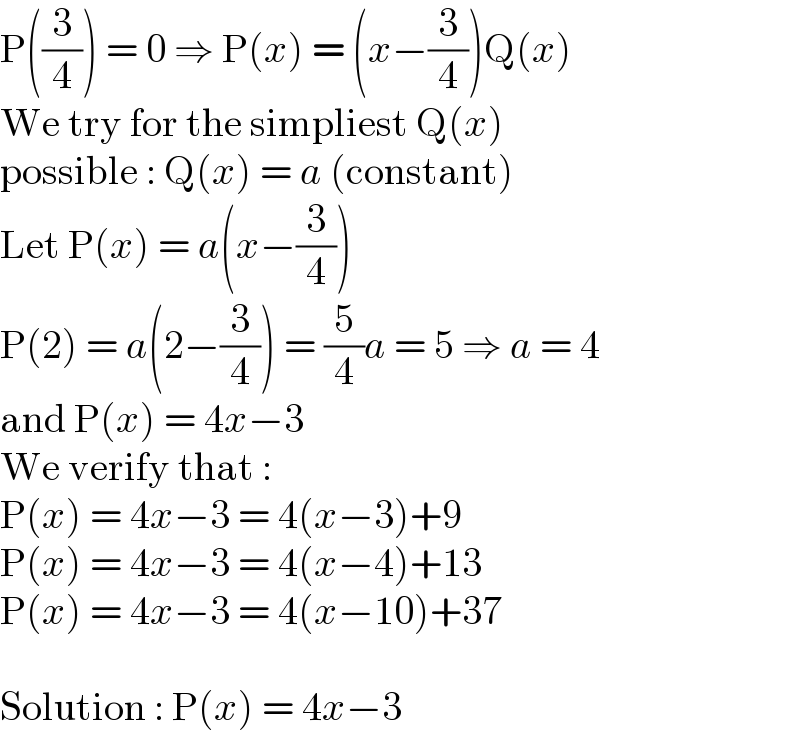
$$\mathrm{P}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\:=\:\mathrm{0}\:\Rightarrow\:\mathrm{P}\left({x}\right)\:=\:\left({x}−\frac{\mathrm{3}}{\mathrm{4}}\right)\mathrm{Q}\left({x}\right) \\ $$ $$\mathrm{We}\:\mathrm{try}\:\mathrm{for}\:\mathrm{the}\:\mathrm{simpliest}\:\mathrm{Q}\left({x}\right) \\ $$ $$\mathrm{possible}\::\:\mathrm{Q}\left({x}\right)\:=\:{a}\:\left(\mathrm{constant}\right) \\ $$ $$\mathrm{Let}\:\mathrm{P}\left({x}\right)\:=\:{a}\left({x}−\frac{\mathrm{3}}{\mathrm{4}}\right) \\ $$ $$\mathrm{P}\left(\mathrm{2}\right)\:=\:{a}\left(\mathrm{2}−\frac{\mathrm{3}}{\mathrm{4}}\right)\:=\:\frac{\mathrm{5}}{\mathrm{4}}{a}\:=\:\mathrm{5}\:\Rightarrow\:{a}\:=\:\mathrm{4} \\ $$ $$\mathrm{and}\:\mathrm{P}\left({x}\right)\:=\:\mathrm{4}{x}−\mathrm{3} \\ $$ $$\mathrm{We}\:\mathrm{verify}\:\mathrm{that}\:: \\ $$ $$\mathrm{P}\left({x}\right)\:=\:\mathrm{4}{x}−\mathrm{3}\:=\:\mathrm{4}\left({x}−\mathrm{3}\right)+\mathrm{9} \\ $$ $$\mathrm{P}\left({x}\right)\:=\:\mathrm{4}{x}−\mathrm{3}\:=\:\mathrm{4}\left({x}−\mathrm{4}\right)+\mathrm{13} \\ $$ $$\mathrm{P}\left({x}\right)\:=\:\mathrm{4}{x}−\mathrm{3}\:=\:\mathrm{4}\left({x}−\mathrm{10}\right)+\mathrm{37} \\ $$ $$ \\ $$ $$\mathrm{Solution}\::\:\mathrm{P}\left({x}\right)\:=\:\mathrm{4}{x}−\mathrm{3} \\ $$
Answered by floor(10²Eta[1]) last updated on 14/Jan/21
+5 f(4)=[b(4)+4]2+5=13 ⇒b(4)=0⇒b(x)=c(x)(x−4) ⇒f(x)=[c(x)(x−4)(x−3)+4](x−2)+5 f(10)=[c(10).42+4]8+5=37 c(10)=0⇒c(x)=0 ⇒f(x)=4x−3](Q129331.png)
$$\mathrm{f}\left(\mathrm{2}\right)=\mathrm{5} \\ $$ $$\mathrm{f}\left(\mathrm{3}\right)=\mathrm{9} \\ $$ $$\mathrm{f}\left(\mathrm{4}\right)=\mathrm{13} \\ $$ $$\mathrm{f}\left(\mathrm{10}\right)=\mathrm{37} \\ $$ $$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{a}\left(\mathrm{x}\right)\left(\mathrm{x}−\mathrm{2}\right)+\mathrm{5} \\ $$ $$\mathrm{f}\left(\mathrm{3}\right)=\mathrm{a}\left(\mathrm{3}\right)+\mathrm{5}=\mathrm{9} \\ $$ $$\Rightarrow\mathrm{a}\left(\mathrm{3}\right)=\mathrm{4}\Rightarrow\mathrm{a}\left(\mathrm{x}\right)=\mathrm{b}\left(\mathrm{x}\right)\left(\mathrm{x}−\mathrm{3}\right)+\mathrm{4} \\ $$ $$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\left[\mathrm{b}\left(\mathrm{x}\right)\left(\mathrm{x}−\mathrm{3}\right)+\mathrm{4}\right]\left(\mathrm{x}−\mathrm{2}\right)+\mathrm{5} \\ $$ $$\mathrm{f}\left(\mathrm{4}\right)=\left[\mathrm{b}\left(\mathrm{4}\right)+\mathrm{4}\right]\mathrm{2}+\mathrm{5}=\mathrm{13} \\ $$ $$\Rightarrow\mathrm{b}\left(\mathrm{4}\right)=\mathrm{0}\Rightarrow\mathrm{b}\left(\mathrm{x}\right)=\mathrm{c}\left(\mathrm{x}\right)\left(\mathrm{x}−\mathrm{4}\right) \\ $$ $$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\left[\mathrm{c}\left(\mathrm{x}\right)\left(\mathrm{x}−\mathrm{4}\right)\left(\mathrm{x}−\mathrm{3}\right)+\mathrm{4}\right]\left(\mathrm{x}−\mathrm{2}\right)+\mathrm{5} \\ $$ $$\mathrm{f}\left(\mathrm{10}\right)=\left[\mathrm{c}\left(\mathrm{10}\right).\mathrm{42}+\mathrm{4}\right]\mathrm{8}+\mathrm{5}=\mathrm{37} \\ $$ $$\mathrm{c}\left(\mathrm{10}\right)=\mathrm{0}\Rightarrow\mathrm{c}\left(\mathrm{x}\right)=\mathrm{0} \\ $$ $$\Rightarrow\mathrm{\color{mathred}{f}}\color{mathred}{\left(}\mathrm{\color{mathred}{x}}\color{mathred}{\right)}\color{mathred}{=}\mathrm{\color{mathred}{4}\color{mathred}{x}}\color{mathred}{−}\mathrm{\color{mathred}{3}} \\ $$
