
Question Number 132402 by bramlexs22 last updated on 14/Feb/21
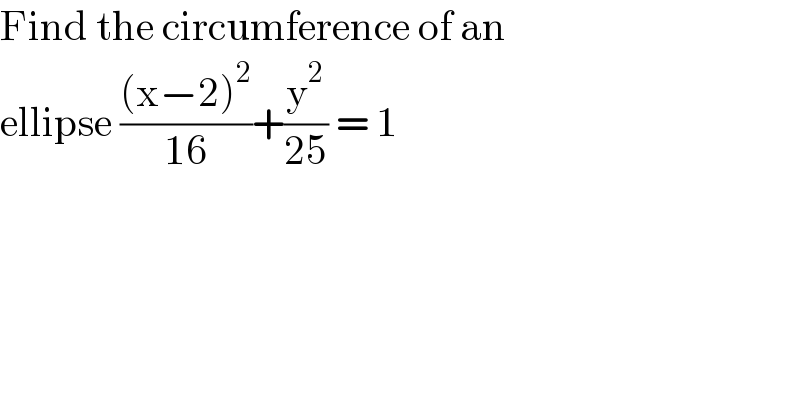
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{circumference}\:\mathrm{of}\:\mathrm{an} \\ $$$$\mathrm{ellipse}\:\frac{\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{16}}+\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{25}}\:=\:\mathrm{1} \\ $$
Commented by mr W last updated on 14/Feb/21

$${the}\:{perimeter}\:{of}\:{an}\:{ellipse}\:{can}\:{not} \\ $$$${be}\:{exactly}\:{calculated}. \\ $$
Commented by mr W last updated on 14/Feb/21

Commented by bramlexs22 last updated on 14/Feb/21

$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by Dwaipayan Shikari last updated on 14/Feb/21
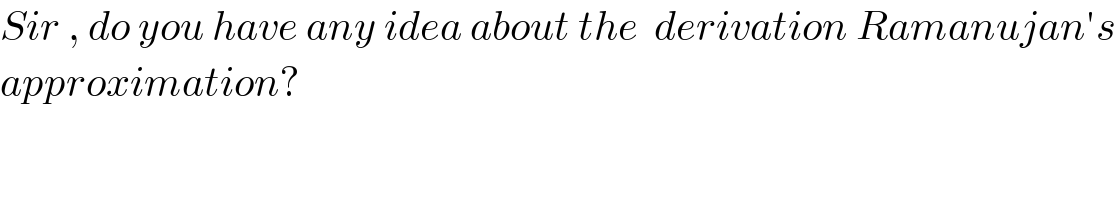
$${Sir}\:,\:{do}\:{you}\:{have}\:{any}\:{idea}\:{about}\:{the}\:\:{derivation}\:{Ramanujan}'{s} \\ $$$${approximation}? \\ $$
Commented by mr W last updated on 14/Feb/21
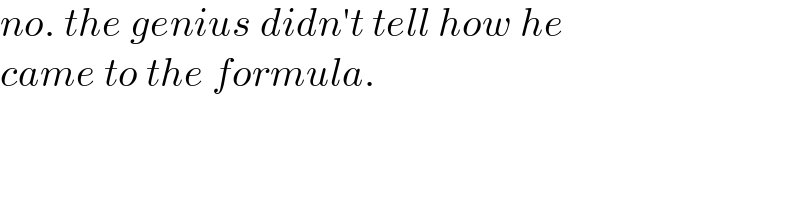
$${no}.\:{the}\:{genius}\:{didn}'{t}\:{tell}\:{how}\:{he} \\ $$$${came}\:{to}\:{the}\:{formula}. \\ $$
Answered by EDWIN88 last updated on 14/Feb/21
![the equation of ellipse (((x−2)^2 )/4^2 ) + (y^2 /5^2 ) = 1 by using formula C = π[ 3(a+b)−(√((3a+b)(a+3b))) ] in this case { ((a=4)),((b=5)) :} ⇒ C = π [ 3(9)−(√((12+5)(4+15))) ] C = π [ 27−(√(17×19)) ] ≈ 28.362](Q132403.png)
$$\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{ellipse}\:\frac{\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{4}^{\mathrm{2}} }\:+\:\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{5}^{\mathrm{2}} }\:=\:\mathrm{1}\: \\ $$$$\mathrm{by}\:\mathrm{using}\:\mathrm{formula}\:\mathrm{C}\:=\:\pi\left[\:\mathrm{3}\left({a}+{b}\right)−\sqrt{\left(\mathrm{3}{a}+{b}\right)\left({a}+\mathrm{3}{b}\right)}\:\right] \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:\begin{cases}{{a}=\mathrm{4}}\\{{b}=\mathrm{5}}\end{cases}\:\Rightarrow\:\mathrm{C}\:=\:\pi\:\left[\:\mathrm{3}\left(\mathrm{9}\right)−\sqrt{\left(\mathrm{12}+\mathrm{5}\right)\left(\mathrm{4}+\mathrm{15}\right)}\:\right] \\ $$$$\:\mathrm{C}\:=\:\pi\:\left[\:\mathrm{27}−\sqrt{\mathrm{17}×\mathrm{19}}\:\right]\:\approx\:\mathrm{28}.\mathrm{362}\: \\ $$
Answered by MJS_new last updated on 14/Feb/21
![length of curve y=c(x) with α≤x≤β we have L=∫_α ^β (√(1+(c′(x))^2 ))dx for y=±(b/a)(√(a^2 −x^2 )) L=(2/a)∫_(−a) ^a (√((a^4 −(a^2 −b^2 )x^2 )/(a^2 −x^2 )))dx= [t=arcsin (x/a) → dx=(√(a^2 −x^2 ))dt] =2a∫_(−π/2) ^(π/2) (√(1−((a^2 −b^2 )/a^2 )sin^2 t)) dt= =2a[E (x∣((a^2 −b^2 )/a^2 ))]_(−π/2) ^(π/2)](Q132417.png)
$$\mathrm{length}\:\mathrm{of}\:\mathrm{curve}\:{y}={c}\left({x}\right)\:\mathrm{with}\:\alpha\leqslant{x}\leqslant\beta\:\mathrm{we}\:\mathrm{have} \\ $$$${L}=\underset{\alpha} {\overset{\beta} {\int}}\sqrt{\mathrm{1}+\left({c}'\left({x}\right)\right)^{\mathrm{2}} }{dx} \\ $$$$\mathrm{for}\:{y}=\pm\frac{{b}}{{a}}\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} } \\ $$$${L}=\frac{\mathrm{2}}{{a}}\underset{−{a}} {\overset{{a}} {\int}}\sqrt{\frac{{a}^{\mathrm{4}} −\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){x}^{\mathrm{2}} }{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{arcsin}\:\frac{{x}}{{a}}\:\rightarrow\:{dx}=\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }{dt}\right] \\ $$$$=\mathrm{2}{a}\underset{−\pi/\mathrm{2}} {\overset{\pi/\mathrm{2}} {\int}}\sqrt{\mathrm{1}−\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\mathrm{sin}^{\mathrm{2}} \:{t}}\:{dt}= \\ $$$$=\mathrm{2}{a}\left[\mathrm{E}\:\left({x}\mid\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)\right]_{−\pi/\mathrm{2}} ^{\pi/\mathrm{2}} \\ $$
Commented by MJS_new last updated on 14/Feb/21
I get approximately 28.3616678890
Answered by Dwaipayan Shikari last updated on 14/Feb/21

$${Perimeter} \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}\Rightarrow\frac{{x}}{{a}^{\mathrm{2}} }=−\frac{{y}}{{b}^{\mathrm{2}} }{y}'\Rightarrow{y}'=−\frac{{bx}}{{a}\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }} \\ $$$${Arc}\:{length}\:=\:\:\int_{−{a}} ^{{a}} \sqrt{\mathrm{1}+\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} }\:{dx} \\ $$$${Perimeter}\:=\mathrm{2}\int_{−{a}} ^{{a}} \sqrt{\mathrm{1}+\frac{{b}^{\mathrm{2}} {x}^{\mathrm{2}} }{{a}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{x}^{\mathrm{2}} \right)}}\:{dx} \\ $$$$=\frac{\mathrm{2}}{{a}}\int_{−{a}} ^{{a}} \sqrt{\frac{{a}^{\mathrm{4}} −{a}^{\mathrm{2}} {x}^{\mathrm{2}} +{b}^{\mathrm{2}} {x}^{\mathrm{2}} }{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}={au} \\ $$$$=\mathrm{2}\int_{−\mathrm{1}} ^{\mathrm{1}} \sqrt{\frac{{a}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{a}^{\mathrm{2}} {u}^{\mathrm{2}} +{b}^{\mathrm{2}} {u}^{\mathrm{2}} \right)}{{a}^{\mathrm{2}} \left(\mathrm{1}−{u}^{\mathrm{2}} \right)}}\:{du}\:\:\:\:\:\: \\ $$$$=\mathrm{2}\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{{a}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta+{b}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta}\:{d}\theta\:\:\: \\ $$$$=\mathrm{2}{a}\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+{e}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}\:{d}\theta=\mathrm{2}{b}\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\mathrm{1}+\frac{{a}^{\mathrm{2}} {e}^{\mathrm{2}} }{{b}^{\mathrm{2}} }{sin}^{\mathrm{2}} \theta}\:{d}\theta \\ $$$$=\mathrm{4}{b}\boldsymbol{\mathrm{E}}\left(\frac{\pi}{\mathrm{2}}\mid\frac{{a}^{\mathrm{2}} {e}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right)\:\:\:\:\:\:\:\:\left({Elliptic}\:{integral}\:{of}\:{first}\:{kind}\right) \\ $$
