Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 132935 by liberty last updated on 17/Feb/21

Answered by EDWIN88 last updated on 17/Feb/21

let x=2 ⇒ f(2).f((1/2))=f(2)+f((1/2)) ⇒ 65.f((1/2)) = 65+f((1/2)) ⇒ f((1/2)) = ((65)/(64)) ⇒ f((1/2))= 1+(1/(64)) ⇒f((1/2)) = 1+(1/2^6 ) ⇒f(x)=1+x^6 then f(−3)=1+(−3)^6 = 730

$$\:\mathrm{let}\:\mathrm{x}=\mathrm{2}\:\Rightarrow\:\mathrm{f}\left(\mathrm{2}\right).\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{f}\left(\mathrm{2}\right)+\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\:\mathrm{65}.\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:\mathrm{65}+\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\:\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:\frac{\mathrm{65}}{\mathrm{64}}\:\Rightarrow\:\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{64}} \\ $$$$\Rightarrow\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{6}} }\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{1}+\mathrm{x}^{\mathrm{6}} \\ $$$$\mathrm{then}\:\mathrm{f}\left(−\mathrm{3}\right)=\mathrm{1}+\left(−\mathrm{3}\right)^{\mathrm{6}} \:=\:\mathrm{730} \\ $$

Answered by Ar Brandon last updated on 17/Feb/21

f(2)=65 therefore f(x) is a non zero polynomial Let f(x)=a_0 +a_1 x+a_2 x^2 +∙∙∙+a_n x^n , a_n ≠0 ⇒(Σ_(r=0) ^n a_r x^r )(Σ_(r=0) ^n (a_r /x^r ))=Σ_(r=0) ^n a_r x^r +Σ_(r=0) ^n (a_r /x^r ) ⇒(Σ_(r=0) ^n a_r x^r )(Σ_(r=0) ^n a_r x^(n−r) )=Σ_(r=0) ^n a_r x^(n+r) +Σ_(r=0) ^n a_r x^(n−r) ⇒(a_0 +a_1 x+a_2 x^2 +∙∙∙+a_n x^n )(a_0 x^n +a_1 x^(n−1) +a_2 x^(n−2) +∙∙∙a_n ) =(a_0 x^n +a_1 x^(n+1) +a_2 x^(n+2) +∙∙∙+a_n x^(2n) )+(a_0 x^n +a_1 x^(n−1) +a_2 x^(n−2) +∙∙∙+a_n ) Comparing coefs we get: a_0 a_n =a_n , a_n ≠0 ⇒a_0 =1 a_0 a_(n−1) +a_1 a_n =a_(n−1) ⇒a_1 =0 a_0 a_(n−2) +a_1 a_(n−1) +a_2 a_n =a_(n−2) ⇒a_2 =0 Continuing this process we get a_1 =a_2 =a_3 =∙∙∙=a_(n−1) =0 For coefs of x^n we have; a_0 ^2 +a_1 ^2 +a_2 ^2 +∙∙∙+a_(n−1) ^2 +a_n ^2 =2a_0 ⇒a_0 ^2 +a_n ^2 =2a_0 ⇒ a_n ^2 =1 ⇒a_n =±1 ⇒f(x)=1±x^n , f(2)=65 ⇒ f(x)=1+x^n ⇒1+2^n =65 ⇒n=6 ⇒f(x)=1+x^6 ⇒f(−3)=1+3^6 =730

$$\mathrm{f}\left(\mathrm{2}\right)=\mathrm{65}\:\mathrm{therefore}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{non}\:\mathrm{zero}\:\mathrm{polynomial} \\ $$$$\mathrm{Let}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{a}_{\mathrm{0}} +\mathrm{a}_{\mathrm{1}} \mathrm{x}+\mathrm{a}_{\mathrm{2}} \mathrm{x}^{\mathrm{2}} +\centerdot\centerdot\centerdot+\mathrm{a}_{\mathrm{n}} \mathrm{x}^{\mathrm{n}} ,\:\mathrm{a}_{\mathrm{n}} \neq\mathrm{0} \\ $$$$\Rightarrow\left(\underset{\mathrm{r}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{a}_{\mathrm{r}} \mathrm{x}^{\mathrm{r}} \right)\left(\underset{\mathrm{r}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{a}_{\mathrm{r}} }{\mathrm{x}^{\mathrm{r}} }\right)=\underset{\mathrm{r}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{a}_{\mathrm{r}} \mathrm{x}^{\mathrm{r}} +\underset{\mathrm{r}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{a}_{\mathrm{r}} }{\mathrm{x}^{\mathrm{r}} } \\ $$$$\Rightarrow\left(\underset{\mathrm{r}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{a}_{\mathrm{r}} \mathrm{x}^{\mathrm{r}} \right)\left(\underset{\mathrm{r}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{a}_{\mathrm{r}} \mathrm{x}^{\mathrm{n}−\mathrm{r}} \right)=\underset{\mathrm{r}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{a}_{\mathrm{r}} \mathrm{x}^{\mathrm{n}+\mathrm{r}} +\underset{\mathrm{r}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{a}_{\mathrm{r}} \mathrm{x}^{\mathrm{n}−\mathrm{r}} \\ $$$$\Rightarrow\left(\mathrm{a}_{\mathrm{0}} +\mathrm{a}_{\mathrm{1}} \mathrm{x}+\mathrm{a}_{\mathrm{2}} \mathrm{x}^{\mathrm{2}} +\centerdot\centerdot\centerdot+\mathrm{a}_{\mathrm{n}} \mathrm{x}^{\mathrm{n}} \right)\left(\mathrm{a}_{\mathrm{0}} \mathrm{x}^{\mathrm{n}} +\mathrm{a}_{\mathrm{1}} \mathrm{x}^{\mathrm{n}−\mathrm{1}} +\mathrm{a}_{\mathrm{2}} \mathrm{x}^{\mathrm{n}−\mathrm{2}} +\centerdot\centerdot\centerdot\mathrm{a}_{\mathrm{n}} \right) \\ $$$$\:\:\:\:\:=\left(\mathrm{a}_{\mathrm{0}} \mathrm{x}^{\mathrm{n}} +\mathrm{a}_{\mathrm{1}} \mathrm{x}^{\mathrm{n}+\mathrm{1}} +\mathrm{a}_{\mathrm{2}} \mathrm{x}^{\mathrm{n}+\mathrm{2}} +\centerdot\centerdot\centerdot+\mathrm{a}_{\mathrm{n}} \mathrm{x}^{\mathrm{2n}} \right)+\left(\mathrm{a}_{\mathrm{0}} \mathrm{x}^{\mathrm{n}} +\mathrm{a}_{\mathrm{1}} \mathrm{x}^{\mathrm{n}−\mathrm{1}} +\mathrm{a}_{\mathrm{2}} \mathrm{x}^{\mathrm{n}−\mathrm{2}} +\centerdot\centerdot\centerdot+\mathrm{a}_{\mathrm{n}} \right) \\ $$$$\mathrm{Comparing}\:\mathrm{coefs}\:\mathrm{we}\:\mathrm{get}: \\ $$$$\mathrm{a}_{\mathrm{0}} \mathrm{a}_{\mathrm{n}} =\mathrm{a}_{\mathrm{n}} ,\:\mathrm{a}_{\mathrm{n}} \neq\mathrm{0}\:\Rightarrow\mathrm{a}_{\mathrm{0}} =\mathrm{1} \\ $$$$\mathrm{a}_{\mathrm{0}} \mathrm{a}_{\mathrm{n}−\mathrm{1}} +\mathrm{a}_{\mathrm{1}} \mathrm{a}_{\mathrm{n}} =\mathrm{a}_{\mathrm{n}−\mathrm{1}} \:\Rightarrow\mathrm{a}_{\mathrm{1}} =\mathrm{0} \\ $$$$\mathrm{a}_{\mathrm{0}} \mathrm{a}_{\mathrm{n}−\mathrm{2}} +\mathrm{a}_{\mathrm{1}} \mathrm{a}_{\mathrm{n}−\mathrm{1}} +\mathrm{a}_{\mathrm{2}} \mathrm{a}_{\mathrm{n}} =\mathrm{a}_{\mathrm{n}−\mathrm{2}} \:\Rightarrow\mathrm{a}_{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{Continuing}\:\mathrm{this}\:\mathrm{process}\:\mathrm{we}\:\mathrm{get}\:\mathrm{a}_{\mathrm{1}} =\mathrm{a}_{\mathrm{2}} =\mathrm{a}_{\mathrm{3}} =\centerdot\centerdot\centerdot=\mathrm{a}_{\mathrm{n}−\mathrm{1}} =\mathrm{0} \\ $$$$\mathrm{For}\:\mathrm{coefs}\:\mathrm{of}\:\mathrm{x}^{\mathrm{n}} \:\mathrm{we}\:\mathrm{have}; \\ $$$$\mathrm{a}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{a}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{a}_{\mathrm{2}} ^{\mathrm{2}} +\centerdot\centerdot\centerdot+\mathrm{a}_{\mathrm{n}−\mathrm{1}} ^{\mathrm{2}} +\mathrm{a}_{\mathrm{n}} ^{\mathrm{2}} =\mathrm{2a}_{\mathrm{0}} \\ $$$$\Rightarrow\mathrm{a}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{a}_{\mathrm{n}} ^{\mathrm{2}} =\mathrm{2a}_{\mathrm{0}} \:\Rightarrow\:\mathrm{a}_{\mathrm{n}} ^{\mathrm{2}} =\mathrm{1}\:\Rightarrow\mathrm{a}_{\mathrm{n}} =\pm\mathrm{1} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{1}\pm\mathrm{x}^{\mathrm{n}} ,\:\mathrm{f}\left(\mathrm{2}\right)=\mathrm{65}\:\Rightarrow\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{1}+\mathrm{x}^{\mathrm{n}} \\ $$$$\Rightarrow\mathrm{1}+\mathrm{2}^{\mathrm{n}} =\mathrm{65}\:\Rightarrow\mathrm{n}=\mathrm{6}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{1}+\mathrm{x}^{\mathrm{6}} \\ $$$$\Rightarrow\mathrm{f}\left(−\mathrm{3}\right)=\mathrm{1}+\mathrm{3}^{\mathrm{6}} =\mathrm{730} \\ $$

Commented by Ar Brandon last updated on 17/Feb/21

What level ?

Commented by Dwaipayan Shikari last updated on 17/Feb/21

When you have added?

$${When}\:{you}\:{have}\:{added}? \\ $$

Commented by Dwaipayan Shikari last updated on 17/Feb/21

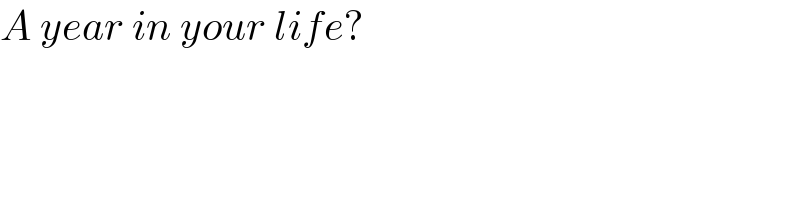
A year in your life?

$${A}\:{year}\:{in}\:{your}\:{life}? \\ $$

Commented by Ar Brandon last updated on 17/Feb/21

Haha ! Let's get inbox, bro. You'll tell me what you're talking about

Commented by Dwaipayan Shikari last updated on 17/Feb/21

What is your birthday? I know it has gone

$${What}\:{is}\:{your}\:{birthday}?\:{I}\:{know}\:{it}\:{has}\:{gone} \\ $$

Commented by Ar Brandon last updated on 18/Feb/21

13/01

Commented by Ar Brandon last updated on 18/Feb/21

When is that ? ��

Commented by Dwaipayan Shikari last updated on 20/Feb/21

(((5^2 −1)/4)+(1/8)(((√(5^2 −1))/(2.1!)))^2 +(1/(12))(((1.3(√(5^2 −1)))/(2^2 .2!)))^2 +(1/(16))(((1.3.5(√(5^2 −1)))/(2^3 .3!)))^2 +....)(∫_(−∞) ^∞ ((sinx)/x)dx)^2

$$\left(\frac{\mathrm{5}^{\mathrm{2}} −\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\sqrt{\mathrm{5}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{2}.\mathrm{1}!}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{12}}\left(\frac{\mathrm{1}.\mathrm{3}\sqrt{\mathrm{5}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{2}^{\mathrm{2}} .\mathrm{2}!}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{16}}\left(\frac{\mathrm{1}.\mathrm{3}.\mathrm{5}\sqrt{\mathrm{5}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{2}^{\mathrm{3}} .\mathrm{3}!}\right)^{\mathrm{2}} +....\right)\left(\int_{−\infty} ^{\infty} \frac{{sinx}}{{x}}{dx}\right)^{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com