Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 135892 by mathmax by abdo last updated on 16/Mar/21

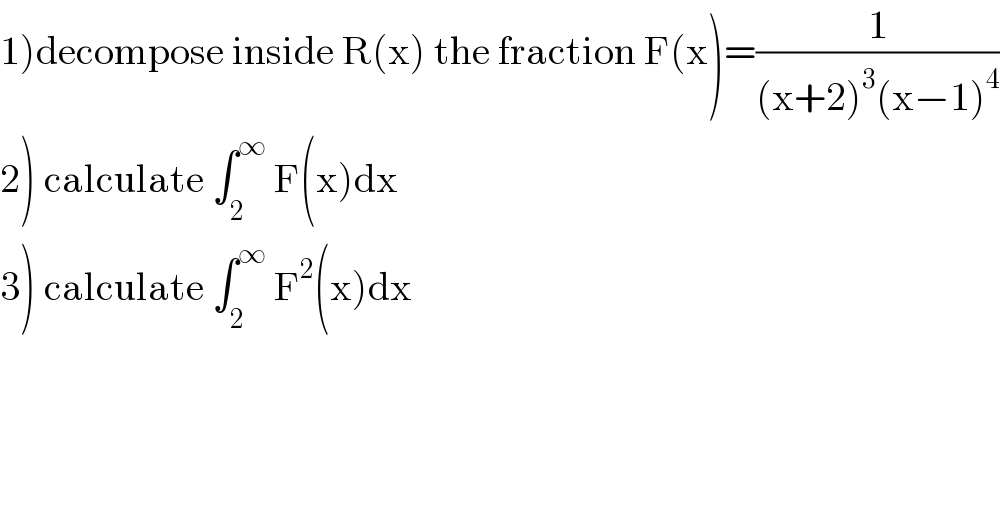
1)decompose inside R(x) the fraction F(x)=(1/((x+2)^3 (x−1)^4 )) 2) calculate ∫_2 ^∞ F(x)dx 3) calculate ∫_2 ^∞ F^2 (x)dx

$$\left.\mathrm{1}\right)\mathrm{decompose}\:\mathrm{inside}\:\mathrm{R}\left(\mathrm{x}\right)\:\mathrm{the}\:\mathrm{fraction}\:\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{3}} \left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$\left.\mathrm{2}\right)\:\mathrm{calculate}\:\int_{\mathrm{2}} ^{\infty} \:\mathrm{F}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\left.\mathrm{3}\right)\:\mathrm{calculate}\:\int_{\mathrm{2}} ^{\infty} \:\mathrm{F}^{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{dx} \\ $$

Answered by mathmax by abdo last updated on 17/Mar/21

1)F(x)=Σ_(i=1) ^3 (a_i /((x+2)^i ))+Σ_(i=1) ^4 (b_i /((x−1)^i )) whst s a_i ? let find D_3 (−2) for f(x)=(x−1)^(−4) f(x)=f(−2) +((x+2)/(1!))f^′ (−2)+(((x+2)^2 )/(2!))f^((2)) (−2)+(((x+2)^3 )/(3!))f^((3)) (−2)+(((x+2)^4 )/(4!))ξ(x) f(−2)=(−3)^(−4) ,f^′ (x)=−4(x−1)^(−5) ⇒f^′ (−2)=−4(−3)^(−5) f^((2)) (x)=20(x−1)^(−6) ⇒f^((2)) (−2)=20(−3)^(−6) f^((3)) (x)=−120(x−1)^(−7) ⇒f^((3)) (−2)=−120(−3)^(−7) ⇒ f(x)=(−3)^(−4) −4(−3)^(−5) (x+2)+((20(−3)^(−6) )/2)(x+2)^2 −((120(−3)^(−7) )/(3!))(x+2)^3 +(((x+2)^4 )/(4!))ξ(x) ⇒ ((f(x))/((x+2)^3 ))=(((−3)^(−4) )/((x+2)^3 ))−((4(−3)^(−5) )/((x+2)^2 )) +((10(−3)^(−6) )/((x+2))) +... ⇒a_1 =10.(−3)^(−6) a_2 =−4(−3)^(−5) ,a_3 =(−3)^(−4) let find b_i we find D_3 (1) for g(x)=(x+2)^(−3) g(x)=g(1)+((x−1)/(1!))g^′ (1) +(((x−1)^2 )/(2!))g^((2)) (1) +(((x−1)^3 )/(3!))g^((3)) (1) +(((x−1)^4 )/(4!))δ(x) g(1)=3^(−3) , g^′ (x)=−3(x+2)^(−4) ⇒g^′ (1)=−3.3^(−4) g^((2)) (x)=12(x+2)^(−5) ⇒g^((2)) (1)=12.3^(−5) g^((3)) (x)=12.5(x+2)^(−6) ⇒g^((3)) (1)=60.3^(−6) g(x)=3^(−3) −3.3^(−4) (x−1)+((12.3^(−5) )/2)(x−1)^2 +((60.3^(−6) )/(3!))(x−1)^3 +... =(1/(27))−(1/(27))(x−1) +(2/(81))(x−1)^2 +10.3^(−6) (x−1)^3 +(((x−1)^4 )/(4!))δ(x) ⇒((g(x))/((x−1)^4 ))=(1/(27(x−1)^4 ))−(1/(27(x−1)^3 ))+(2/(81(x−1)^2 ))+((10.3^(−6) )/(x−1)) ⇒ b_1 =10.3^(−6) , b_2 =(2/(81)) ,b_3 =−(1/(27)) ,b_4 =(1/(27)) ⇒

$$\left.\mathrm{1}\right)\mathrm{F}\left(\mathrm{x}\right)=\sum_{\mathrm{i}=\mathrm{1}} ^{\mathrm{3}} \:\frac{\mathrm{a}_{\mathrm{i}} }{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{i}} }+\sum_{\mathrm{i}=\mathrm{1}} ^{\mathrm{4}} \:\frac{\mathrm{b}_{\mathrm{i}} }{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{i}} }\:\:\:\:\mathrm{whst}\:\mathrm{s}\:\mathrm{a}_{\mathrm{i}} ? \\ $$$$\mathrm{let}\:\mathrm{find}\:\mathrm{D}_{\mathrm{3}} \left(−\mathrm{2}\right)\:\mathrm{for}\:\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{x}−\mathrm{1}\right)^{−\mathrm{4}} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(−\mathrm{2}\right)\:+\frac{\mathrm{x}+\mathrm{2}}{\mathrm{1}!}\mathrm{f}^{'} \left(−\mathrm{2}\right)+\frac{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{2}!}\mathrm{f}^{\left(\mathrm{2}\right)} \left(−\mathrm{2}\right)+\frac{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{3}} }{\mathrm{3}!}\mathrm{f}^{\left(\mathrm{3}\right)} \left(−\mathrm{2}\right)+\frac{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{4}} }{\mathrm{4}!}\xi\left(\mathrm{x}\right) \\ $$$$\mathrm{f}\left(−\mathrm{2}\right)=\left(−\mathrm{3}\right)^{−\mathrm{4}} \:,\mathrm{f}^{'} \left(\mathrm{x}\right)=−\mathrm{4}\left(\mathrm{x}−\mathrm{1}\right)^{−\mathrm{5}} \:\Rightarrow\mathrm{f}^{'} \left(−\mathrm{2}\right)=−\mathrm{4}\left(−\mathrm{3}\right)^{−\mathrm{5}} \\ $$$$\mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)=\mathrm{20}\left(\mathrm{x}−\mathrm{1}\right)^{−\mathrm{6}} \:\Rightarrow\mathrm{f}^{\left(\mathrm{2}\right)} \left(−\mathrm{2}\right)=\mathrm{20}\left(−\mathrm{3}\right)^{−\mathrm{6}} \\ $$$$\mathrm{f}^{\left(\mathrm{3}\right)} \left(\mathrm{x}\right)=−\mathrm{120}\left(\mathrm{x}−\mathrm{1}\right)^{−\mathrm{7}} \Rightarrow\mathrm{f}^{\left(\mathrm{3}\right)} \left(−\mathrm{2}\right)=−\mathrm{120}\left(−\mathrm{3}\right)^{−\mathrm{7}} \:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\left(−\mathrm{3}\right)^{−\mathrm{4}} \:−\mathrm{4}\left(−\mathrm{3}\right)^{−\mathrm{5}} \left(\mathrm{x}+\mathrm{2}\right)+\frac{\mathrm{20}\left(−\mathrm{3}\right)^{−\mathrm{6}} }{\mathrm{2}}\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} −\frac{\mathrm{120}\left(−\mathrm{3}\right)^{−\mathrm{7}} }{\mathrm{3}!}\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{3}} \\ $$$$+\frac{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{4}} }{\mathrm{4}!}\xi\left(\mathrm{x}\right)\:\Rightarrow \\ $$$$\frac{\mathrm{f}\left(\mathrm{x}\right)}{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{3}} }=\frac{\left(−\mathrm{3}\right)^{−\mathrm{4}} }{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{3}} }−\frac{\mathrm{4}\left(−\mathrm{3}\right)^{−\mathrm{5}} }{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{2}} }\:+\frac{\mathrm{10}\left(−\mathrm{3}\right)^{−\mathrm{6}} }{\left(\mathrm{x}+\mathrm{2}\right)}\:+...\:\Rightarrow\mathrm{a}_{\mathrm{1}} =\mathrm{10}.\left(−\mathrm{3}\right)^{−\mathrm{6}} \\ $$$$\mathrm{a}_{\mathrm{2}} =−\mathrm{4}\left(−\mathrm{3}\right)^{−\mathrm{5}} \:\:,\mathrm{a}_{\mathrm{3}} =\left(−\mathrm{3}\right)^{−\mathrm{4}} \:\mathrm{let}\:\mathrm{find}\:\mathrm{b}_{\mathrm{i}} \:\:\:\mathrm{we}\:\mathrm{find}\:\mathrm{D}_{\mathrm{3}} \left(\mathrm{1}\right)\:\mathrm{for}\:\mathrm{g}\left(\mathrm{x}\right)=\left(\mathrm{x}+\mathrm{2}\right)^{−\mathrm{3}} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)=\mathrm{g}\left(\mathrm{1}\right)+\frac{\mathrm{x}−\mathrm{1}}{\mathrm{1}!}\mathrm{g}^{'} \left(\mathrm{1}\right)\:+\frac{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}!}\mathrm{g}^{\left(\mathrm{2}\right)} \left(\mathrm{1}\right)\:+\frac{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{3}!}\mathrm{g}^{\left(\mathrm{3}\right)} \left(\mathrm{1}\right)\:+\frac{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{4}} }{\mathrm{4}!}\delta\left(\mathrm{x}\right) \\ $$$$\mathrm{g}\left(\mathrm{1}\right)=\mathrm{3}^{−\mathrm{3}} \:\:\:\:,\:\mathrm{g}^{'} \left(\mathrm{x}\right)=−\mathrm{3}\left(\mathrm{x}+\mathrm{2}\right)^{−\mathrm{4}} \:\Rightarrow\mathrm{g}^{'} \left(\mathrm{1}\right)=−\mathrm{3}.\mathrm{3}^{−\mathrm{4}} \\ $$$$\mathrm{g}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)=\mathrm{12}\left(\mathrm{x}+\mathrm{2}\right)^{−\mathrm{5}} \:\Rightarrow\mathrm{g}^{\left(\mathrm{2}\right)} \left(\mathrm{1}\right)=\mathrm{12}.\mathrm{3}^{−\mathrm{5}} \:\mathrm{g}^{\left(\mathrm{3}\right)} \left(\mathrm{x}\right)=\mathrm{12}.\mathrm{5}\left(\mathrm{x}+\mathrm{2}\right)^{−\mathrm{6}} \:\Rightarrow\mathrm{g}^{\left(\mathrm{3}\right)} \left(\mathrm{1}\right)=\mathrm{60}.\mathrm{3}^{−\mathrm{6}} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)=\mathrm{3}^{−\mathrm{3}} \:−\mathrm{3}.\mathrm{3}^{−\mathrm{4}} \left(\mathrm{x}−\mathrm{1}\right)+\frac{\mathrm{12}.\mathrm{3}^{−\mathrm{5}} }{\mathrm{2}}\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} +\frac{\mathrm{60}.\mathrm{3}^{−\mathrm{6}} }{\mathrm{3}!}\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{3}} \:+... \\ $$$$=\frac{\mathrm{1}}{\mathrm{27}}−\frac{\mathrm{1}}{\mathrm{27}}\left(\mathrm{x}−\mathrm{1}\right)\:+\frac{\mathrm{2}}{\mathrm{81}}\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{10}.\mathrm{3}^{−\mathrm{6}} \left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{3}} \:+\frac{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{4}} }{\mathrm{4}!}\delta\left(\mathrm{x}\right) \\ $$$$\Rightarrow\frac{\mathrm{g}\left(\mathrm{x}\right)}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{4}} }=\frac{\mathrm{1}}{\mathrm{27}\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{4}} }−\frac{\mathrm{1}}{\mathrm{27}\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{2}}{\mathrm{81}\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{10}.\mathrm{3}^{−\mathrm{6}} }{\mathrm{x}−\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{b}_{\mathrm{1}} =\mathrm{10}.\mathrm{3}^{−\mathrm{6}} \:,\:\mathrm{b}_{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{81}}\:\:,\mathrm{b}_{\mathrm{3}} =−\frac{\mathrm{1}}{\mathrm{27}}\:,\mathrm{b}_{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{27}}\:\Rightarrow \\ $$$$ \\ $$

Answered by mathmax by abdo last updated on 17/Mar/21

2) ∫_2 ^∞ (dx/((x+2)^3 (x−1)^4 )) =∫_2 ^∞ (dx/((((x−1)/(x+2)))^4 (x+2)^7 )) we do the changement ((x−1)/(x+2))=t ⇒x−1=tx+2t ⇒(1−t)x=1+2t ⇒x=((1+2t)/(1−t)) ⇒ (dx/dt)=((2(1−t)−(1+2t)(−1))/((1−t)^2 ))=((2−2t+1+2t )/((1−t)^2 ))=(3/((1−t)^2 )) x+2=((1+2t)/(1−t))+2=((1+2t+2−2t)/(1−t))=(3/(1−t)) ⇒ I=∫_(1/4) ^1 (1/(t^4 ((3/(1−t)))^7 ))((3dt)/((1−t)^2 )) =(1/3^6 )∫_(1/4) ^1 (((1−t)^7 )/(t^4 (1−t)^2 ))dt =(1/3^6 )∫_(1/4) ^1 (((1−t)^5 )/t^4 )dt =−(1/3^6 )∫_(1/4) ^1 ((Σ_(k=0) ^5 C_5 ^k t^k (−1)^(5−k) )/t^4 )dt =(1/3^6 ) Σ_(k=0) ^5 (−1)^k C_5 ^k ∫_(1/4) ^1 t^(k−4) dt =(1/3^6 )Σ_(k=0 and k≠3) ^5 (−1)^k C_5 ^k [(1/(k−3))t^(k−3) ]_(1/4) ^1 −(1/3^6 )C_5 ^3 [ln∣t∣]_(1/4) ^1 =(1/3^6 )Σ_(k=0 and k≠3) ^5 (((−1)^k C_5 ^k )/(k−3))(1−(1/4^(k−3) ))+(1/3^6 )C_5 ^3 (2ln(2))

$$\left.\mathrm{2}\right)\:\int_{\mathrm{2}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{3}} \left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{4}} }\:=\int_{\mathrm{2}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{2}}\right)^{\mathrm{4}} \left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{7}} }\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement} \\ $$$$\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{2}}=\mathrm{t}\:\Rightarrow\mathrm{x}−\mathrm{1}=\mathrm{tx}+\mathrm{2t}\:\:\Rightarrow\left(\mathrm{1}−\mathrm{t}\right)\mathrm{x}=\mathrm{1}+\mathrm{2t}\:\Rightarrow\mathrm{x}=\frac{\mathrm{1}+\mathrm{2t}}{\mathrm{1}−\mathrm{t}}\:\Rightarrow \\ $$$$\frac{\mathrm{dx}}{\mathrm{dt}}=\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{t}\right)−\left(\mathrm{1}+\mathrm{2t}\right)\left(−\mathrm{1}\right)}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }=\frac{\mathrm{2}−\mathrm{2t}+\mathrm{1}+\mathrm{2t}\:}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }=\frac{\mathrm{3}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} } \\ $$$$\mathrm{x}+\mathrm{2}=\frac{\mathrm{1}+\mathrm{2t}}{\mathrm{1}−\mathrm{t}}+\mathrm{2}=\frac{\mathrm{1}+\mathrm{2t}+\mathrm{2}−\mathrm{2t}}{\mathrm{1}−\mathrm{t}}=\frac{\mathrm{3}}{\mathrm{1}−\mathrm{t}}\:\Rightarrow \\ $$$$\mathrm{I}=\int_{\frac{\mathrm{1}}{\mathrm{4}}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{4}} \left(\frac{\mathrm{3}}{\mathrm{1}−\mathrm{t}}\right)^{\mathrm{7}} }\frac{\mathrm{3dt}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{6}} }\int_{\frac{\mathrm{1}}{\mathrm{4}}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{7}} }{\mathrm{t}^{\mathrm{4}} \left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{6}} }\int_{\frac{\mathrm{1}}{\mathrm{4}}} ^{\mathrm{1}} \:\frac{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{5}} }{\mathrm{t}^{\mathrm{4}} }\mathrm{dt}\:=−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{6}} }\int_{\frac{\mathrm{1}}{\mathrm{4}}} ^{\mathrm{1}} \:\frac{\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{5}} \:\mathrm{C}_{\mathrm{5}} ^{\mathrm{k}} \:\mathrm{t}^{\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{5}−\mathrm{k}} }{\mathrm{t}^{\mathrm{4}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{6}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{5}} \:\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{5}} ^{\mathrm{k}} \:\int_{\frac{\mathrm{1}}{\mathrm{4}}} ^{\mathrm{1}} \:\mathrm{t}^{\mathrm{k}−\mathrm{4}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{6}} }\sum_{\mathrm{k}=\mathrm{0}\:\mathrm{and}\:\mathrm{k}\neq\mathrm{3}} ^{\mathrm{5}} \:\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{5}} ^{\mathrm{k}} \:\left[\frac{\mathrm{1}}{\mathrm{k}−\mathrm{3}}\mathrm{t}^{\mathrm{k}−\mathrm{3}} \right]_{\frac{\mathrm{1}}{\mathrm{4}}} ^{\mathrm{1}} \:−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{6}} }\mathrm{C}_{\mathrm{5}} ^{\mathrm{3}} \left[\mathrm{ln}\mid\mathrm{t}\mid\right]_{\frac{\mathrm{1}}{\mathrm{4}}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{6}} }\sum_{\mathrm{k}=\mathrm{0}\:\mathrm{and}\:\mathrm{k}\neq\mathrm{3}} ^{\mathrm{5}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{5}} ^{\mathrm{k}} }{\mathrm{k}−\mathrm{3}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{k}−\mathrm{3}} }\right)+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{6}} }\mathrm{C}_{\mathrm{5}} ^{\mathrm{3}} \left(\mathrm{2ln}\left(\mathrm{2}\right)\right) \\ $$

Commented by mathmax by abdo last updated on 17/Mar/21

let Φ=∫_2 ^∞ F^2 (x)dx ⇒Φ =∫_2 ^∞ (dx/((x+2)^6 (x−1)^8 )) =∫_2 ^∞ (dx/((((x−1)/(x+2)))^8 (x+2)^(14) )) chamgement ((x−1)/(x+2))=t give Φ =∫_(1/4) ^1 (1/(t^8 ((3/(1−t)))^(14) ))((3dt)/((1−t)^2 )) =(1/3^(13) ) ∫_(1/4) ^1 (((1−t)^(12) )/t^8 )dt =(1/3^(13) )∫_(1/4) ^1 (1/t^8 )Σ_(k=0) ^(12) C_(12) ^k t^k (−1)^(12−k) dt =(1/3^(13) )Σ_(k=0) ^(12) (−1)^k C_(12) ^k ∫_(1/4) ^1 t^(k−8) dt =(1/3^(13) ) Σ_(k=0 and k≠7) ^(12) (−1)^k C_(12) ^k [(1/(k−7))t^(k−7) ]_(1/4) ^1 − (1/3^(13) )C_(12) ^7 [ln∣t∣]_(1/4) ^1 Φ=(1/3^(13) )Σ_(k=0 and k≠7) ^(12) (((−1)^k C_(12) ^k )/(k−7))(1−(1/4^(k−7) ))+(1/3^(13) )C_(12) ^7 (2ln(2))

$$\mathrm{let}\:\Phi=\int_{\mathrm{2}} ^{\infty} \:\mathrm{F}^{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{dx}\:\Rightarrow\Phi\:=\int_{\mathrm{2}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{6}} \left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{8}} } \\ $$$$=\int_{\mathrm{2}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{2}}\right)^{\mathrm{8}} \left(\mathrm{x}+\mathrm{2}\right)^{\mathrm{14}} }\:\:\mathrm{chamgement}\:\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{2}}=\mathrm{t}\:\mathrm{give} \\ $$$$\Phi\:=\int_{\frac{\mathrm{1}}{\mathrm{4}}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{8}} \left(\frac{\mathrm{3}}{\mathrm{1}−\mathrm{t}}\right)^{\mathrm{14}} }\frac{\mathrm{3dt}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{13}} }\:\int_{\frac{\mathrm{1}}{\mathrm{4}}} ^{\mathrm{1}} \:\frac{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{12}} }{\mathrm{t}^{\mathrm{8}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{13}} }\int_{\frac{\mathrm{1}}{\mathrm{4}}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{8}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{12}} \:\mathrm{C}_{\mathrm{12}} ^{\mathrm{k}} \:\mathrm{t}^{\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{12}−\mathrm{k}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{13}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{12}} \:\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{12}} ^{\mathrm{k}} \:\int_{\frac{\mathrm{1}}{\mathrm{4}}} ^{\mathrm{1}} \:\mathrm{t}^{\mathrm{k}−\mathrm{8}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{13}} }\:\sum_{\mathrm{k}=\mathrm{0}\:\mathrm{and}\:\mathrm{k}\neq\mathrm{7}} ^{\mathrm{12}} \:\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{12}} ^{\mathrm{k}} \:\left[\frac{\mathrm{1}}{\mathrm{k}−\mathrm{7}}\mathrm{t}^{\mathrm{k}−\mathrm{7}} \right]_{\frac{\mathrm{1}}{\mathrm{4}}} ^{\mathrm{1}} −\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{13}} }\mathrm{C}_{\mathrm{12}} ^{\mathrm{7}} \:\left[\mathrm{ln}\mid\mathrm{t}\mid\right]_{\frac{\mathrm{1}}{\mathrm{4}}} ^{\mathrm{1}} \\ $$$$\Phi=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{13}} }\sum_{\mathrm{k}=\mathrm{0}\:\mathrm{and}\:\mathrm{k}\neq\mathrm{7}} ^{\mathrm{12}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{12}} ^{\mathrm{k}} }{\mathrm{k}−\mathrm{7}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{k}−\mathrm{7}} }\right)+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{13}} }\mathrm{C}_{\mathrm{12}} ^{\mathrm{7}} \left(\mathrm{2ln}\left(\mathrm{2}\right)\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com