Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 138085 by liberty last updated on 10/Apr/21

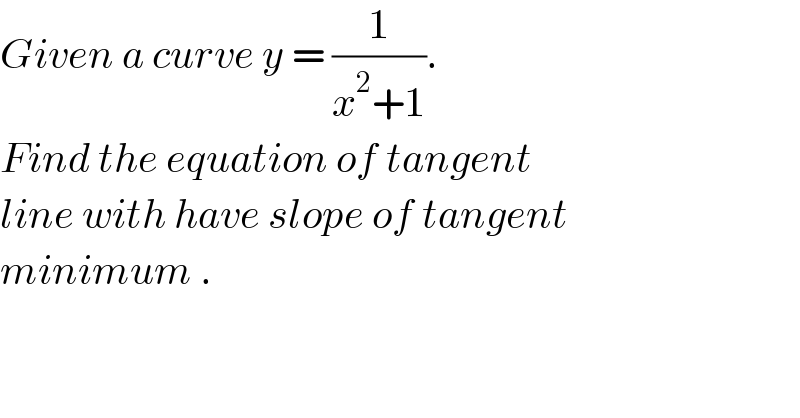
Given a curve y = (1/(x^2 +1)). Find the equation of tangent line with have slope of tangent minimum .

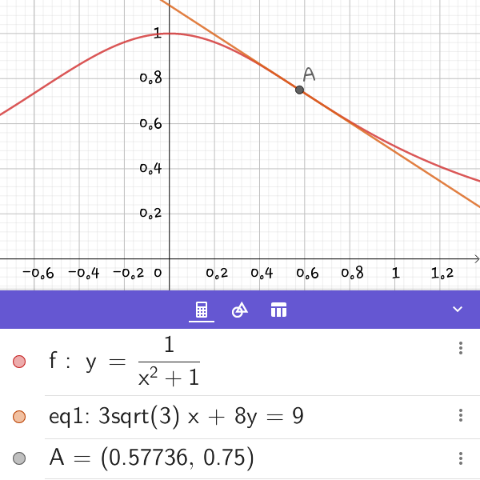
$${Given}\:{a}\:{curve}\:{y}\:=\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}. \\ $$$${Find}\:{the}\:{equation}\:{of}\:{tangent} \\ $$$${line}\:{with}\:{have}\:{slope}\:{of}\:{tangent} \\ $$$${minimum}\:. \\ $$

Answered by EDWIN88 last updated on 10/Apr/21

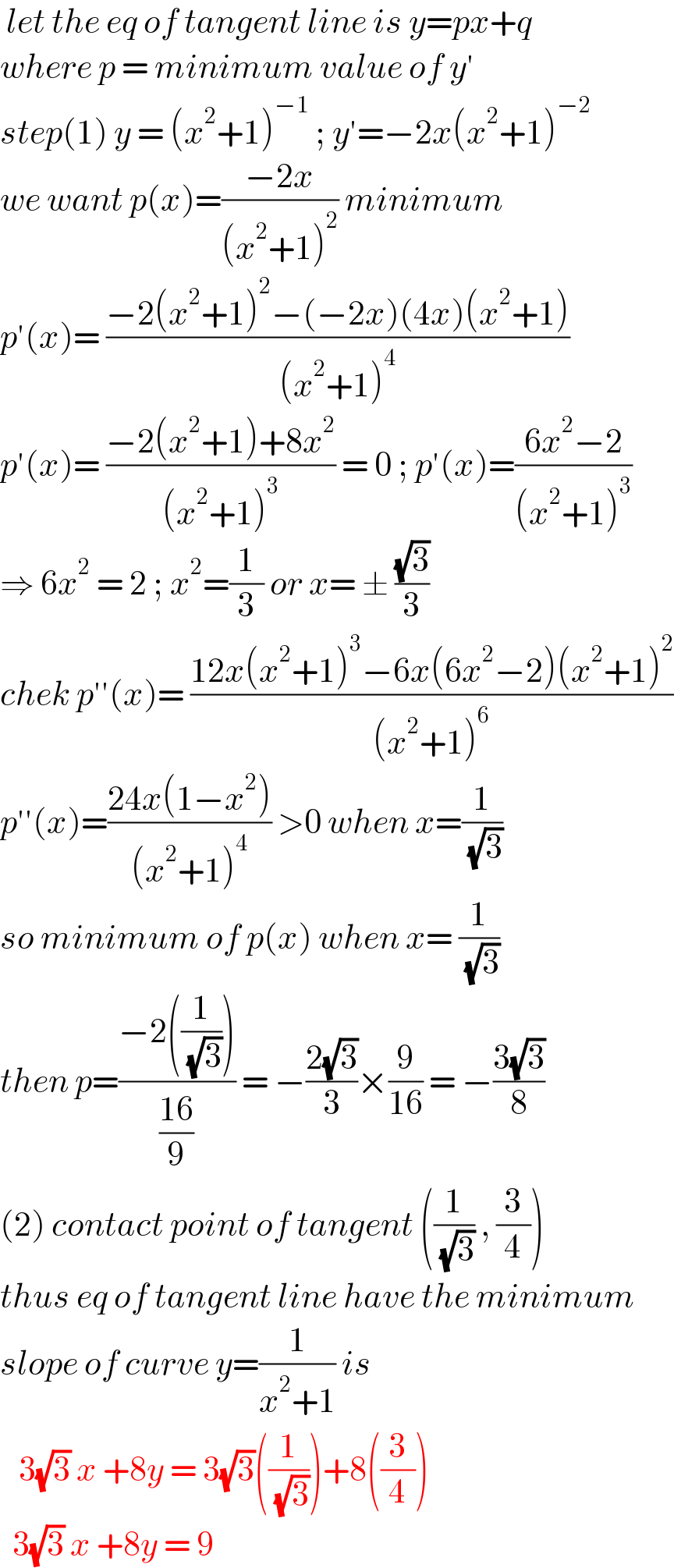
let the eq of tangent line is y=px+q where p = minimum value of y′ step(1) y = (x^2 +1)^(−1) ; y′=−2x(x^2 +1)^(−2) we want p(x)=((−2x)/((x^2 +1)^2 )) minimum p′(x)= ((−2(x^2 +1)^2 −(−2x)(4x)(x^2 +1))/((x^2 +1)^4 )) p′(x)= ((−2(x^2 +1)+8x^2 )/((x^2 +1)^3 )) = 0 ; p′(x)=((6x^2 −2)/((x^2 +1)^3 )) ⇒ 6x^2 = 2 ; x^2 =(1/3) or x= ± ((√3)/3) chek p′′(x)= ((12x(x^2 +1)^3 −6x(6x^2 −2)(x^2 +1)^2 )/((x^2 +1)^6 )) p′′(x)=((24x(1−x^2 ))/((x^2 +1)^4 )) >0 when x=(1/( (√3))) so minimum of p(x) when x= (1/( (√3))) then p=((−2((1/( (√3)))))/((16)/9)) = −((2(√3))/3)×(9/(16)) = −((3(√3))/8) (2) contact point of tangent ((1/( (√3))) , (3/4)) thus eq of tangent line have the minimum slope of curve y=(1/(x^2 +1)) is 3(√3) x +8y = 3(√3)((1/( (√3))))+8((3/4)) 3(√3) x +8y = 9

$$\:{let}\:{the}\:{eq}\:{of}\:{tangent}\:{line}\:{is}\:{y}={px}+{q} \\ $$$${where}\:{p}\:=\:{minimum}\:{value}\:{of}\:{y}' \\ $$$${step}\left(\mathrm{1}\right)\:{y}\:=\:\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{−\mathrm{1}} \:;\:{y}'=−\mathrm{2}{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{−\mathrm{2}} \\ $$$${we}\:{want}\:{p}\left({x}\right)=\frac{−\mathrm{2}{x}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:{minimum} \\ $$$${p}'\left({x}\right)=\:\frac{−\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −\left(−\mathrm{2}{x}\right)\left(\mathrm{4}{x}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{4}} } \\ $$$${p}'\left({x}\right)=\:\frac{−\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{1}\right)+\mathrm{8}{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }\:=\:\mathrm{0}\:;\:{p}'\left({x}\right)=\frac{\mathrm{6}{x}^{\mathrm{2}} −\mathrm{2}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\Rightarrow\:\mathrm{6}{x}^{\mathrm{2}} \:=\:\mathrm{2}\:;\:{x}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{3}}\:{or}\:{x}=\:\pm\:\frac{\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$${chek}\:{p}''\left({x}\right)=\:\frac{\mathrm{12}{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} −\mathrm{6}{x}\left(\mathrm{6}{x}^{\mathrm{2}} −\mathrm{2}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{6}} } \\ $$$${p}''\left({x}\right)=\frac{\mathrm{24}{x}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{4}} }\:>\mathrm{0}\:{when}\:{x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$${so}\:{minimum}\:{of}\:{p}\left({x}\right)\:{when}\:{x}=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$${then}\:{p}=\frac{−\mathrm{2}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)}{\frac{\mathrm{16}}{\mathrm{9}}}\:=\:−\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}×\frac{\mathrm{9}}{\mathrm{16}}\:=\:−\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}} \\ $$$$\left(\mathrm{2}\right)\:{contact}\:{point}\:{of}\:{tangent}\:\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:,\:\frac{\mathrm{3}}{\mathrm{4}}\right) \\ $$$${thus}\:{eq}\:{of}\:{tangent}\:{line}\:{have}\:{the}\:{minimum} \\ $$$${slope}\:{of}\:{curve}\:{y}=\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}\:{is}\: \\ $$$$\:\:\:\mathrm{3}\sqrt{\mathrm{3}}\:{x}\:+\mathrm{8}{y}\:=\:\mathrm{3}\sqrt{\mathrm{3}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+\mathrm{8}\left(\frac{\mathrm{3}}{\mathrm{4}}\right) \\ $$$$\:\:\mathrm{3}\sqrt{\mathrm{3}}\:{x}\:+\mathrm{8}{y}\:=\:\mathrm{9}\: \\ $$

Commented by EDWIN88 last updated on 10/Apr/21

Terms of Service

Privacy Policy

Contact: info@tinkutara.com