
Question Number 138742 by mnjuly1970 last updated on 17/Apr/21
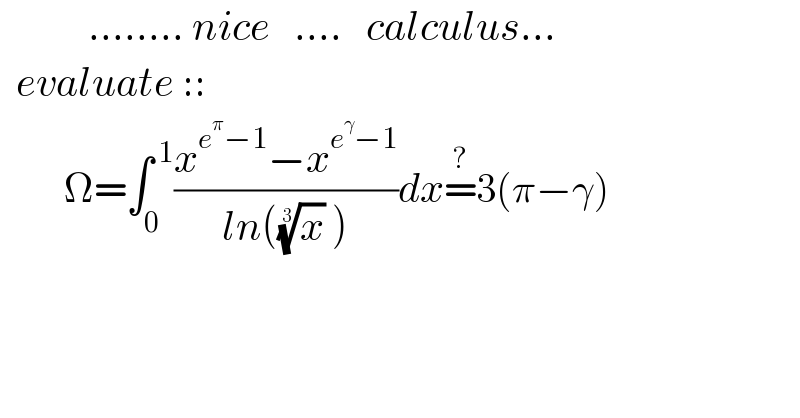
$$\:\:\:\:\:\:\:\:\:\:\:........\:{nice}\:\:\:....\:\:\:{calculus}... \\ $$$$\:\:{evaluate}\::: \\ $$$$\:\:\:\:\:\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{x}^{{e}^{\pi} −\mathrm{1}} −{x}^{{e}^{\gamma} −\mathrm{1}} }{{ln}\left(\sqrt[{\mathrm{3}}]{{x}}\:\right)}{dx}\overset{?} {=}\mathrm{3}\left(\pi−\gamma\right) \\ $$
Answered by Dwaipayan Shikari last updated on 17/Apr/21

$$\mathrm{3}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{e}^{\pi} −\mathrm{1}} −{x}^{{e}^{\gamma} −\mathrm{1}} }{{log}\left({x}\right)}{dx}=\mathrm{3}\chi\left({e}^{\pi} −\mathrm{1},{e}^{\gamma} −\mathrm{1}\right)=\mathrm{3}\left(\pi−\gamma\right) \\ $$$$\chi\left({a},{b}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{a}} −{x}^{{b}} }{{log}\left({x}\right)}{dx} \\ $$$$\frac{\partial}{\partial{a}}\chi\left({a},{b}\right)=\frac{\mathrm{1}}{{a}+\mathrm{1}}\Rightarrow\chi\left({a},{b}\right)={log}\left({a}+\mathrm{1}\right)+{C} \\ $$$$\chi\left({b},{b}\right)=\mathrm{0}\:\Rightarrow{C}=−{log}\left({b}+\mathrm{1}\right)\:\:\Rightarrow\chi\left({a},{b}\right)={log}\left(\frac{{a}+\mathrm{1}}{{b}+\mathrm{1}}\right) \\ $$
Commented by Ar Brandon last updated on 17/Apr/21

$$\mathrm{Wow}\:\mathrm{cool}!\:\mathrm{I}\:\mathrm{was}\:\mathrm{supposed}\:\mathrm{to}\:\mathrm{remain}\:\mathrm{at} \\ $$$$\mathrm{the}\:\mathrm{first}\:\mathrm{power}. \\ $$
Commented by mnjuly1970 last updated on 17/Apr/21

$${tashakor}\:...{mercey}.. \\ $$
Answered by Ar Brandon last updated on 17/Apr/21
![Ω=∫_0 ^1 ((x^(e^π −1) −x^(e^γ −1) )/(ln((x)^(1/3) )))dx, u=x^(1/3) ⇒3u^2 du=dx =∫_0 ^1 ((u^(3(e^π −1)) −u^(3(e^γ −1)) )/(ln(u)))(3u^2 du)=3∫_0 ^1 ((u^(3e^π −1) −u^(3e^γ −1) )/(ln(u)))du f(α)=3∫_0 ^1 ((u^(3e^π +α) −u^(3e^γ +α) )/(ln(u)))du f ′(α)=3∫_0 ^1 (u^(3e^π +α) −u^(3e^γ +α) )du =3[(u^(3e^π +α+1) /(3e^π +α+1))−(u^(3e^γ +α+1) /(3e^γ +α+1))]_0 ^1 =3[(1/(3e^π +α+1))−(1/(3e^γ +α+1))] f(α)=3ln(3e^π +α+1)−3ln(3e^γ +α+1)+C](Q138746.png)
$$\Omega=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}^{\mathrm{e}^{\pi} −\mathrm{1}} −\mathrm{x}^{\mathrm{e}^{\gamma} −\mathrm{1}} }{\mathrm{ln}\left(\sqrt[{\mathrm{3}}]{\mathrm{x}}\right)}\mathrm{dx},\:\mathrm{u}=\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{3}}} \Rightarrow\mathrm{3u}^{\mathrm{2}} \mathrm{du}=\mathrm{dx} \\ $$$$\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{u}^{\mathrm{3}\left(\mathrm{e}^{\pi} −\mathrm{1}\right)} −\mathrm{u}^{\mathrm{3}\left(\mathrm{e}^{\gamma} −\mathrm{1}\right)} }{\mathrm{ln}\left(\mathrm{u}\right)}\left(\mathrm{3u}^{\mathrm{2}} \mathrm{du}\right)=\mathrm{3}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{u}^{\mathrm{3e}^{\pi} −\mathrm{1}} −\mathrm{u}^{\mathrm{3e}^{\gamma} −\mathrm{1}} }{\mathrm{ln}\left(\mathrm{u}\right)}\mathrm{du} \\ $$$$\mathrm{f}\left(\alpha\right)=\mathrm{3}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{u}^{\mathrm{3e}^{\pi} +\alpha} −\mathrm{u}^{\mathrm{3e}^{\gamma} +\alpha} }{\mathrm{ln}\left(\mathrm{u}\right)}\mathrm{du} \\ $$$$\mathrm{f}\:'\left(\alpha\right)=\mathrm{3}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{u}^{\mathrm{3e}^{\pi} +\alpha} −\mathrm{u}^{\mathrm{3e}^{\gamma} +\alpha} \right)\mathrm{du} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{3}\left[\frac{\mathrm{u}^{\mathrm{3e}^{\pi} +\alpha+\mathrm{1}} }{\mathrm{3e}^{\pi} +\alpha+\mathrm{1}}−\frac{\mathrm{u}^{\mathrm{3e}^{\gamma} +\alpha+\mathrm{1}} }{\mathrm{3e}^{\gamma} +\alpha+\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:\:\:=\mathrm{3}\left[\frac{\mathrm{1}}{\mathrm{3e}^{\pi} +\alpha+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{3e}^{\gamma} +\alpha+\mathrm{1}}\right] \\ $$$$\mathrm{f}\left(\alpha\right)=\mathrm{3ln}\left(\mathrm{3e}^{\pi} +\alpha+\mathrm{1}\right)−\mathrm{3ln}\left(\mathrm{3e}^{\gamma} +\alpha+\mathrm{1}\right)+\mathrm{C} \\ $$
Commented by mnjuly1970 last updated on 17/Apr/21

$${thanks}\:{alot}... \\ $$
