
Question Number 139313 by Dwaipayan Shikari last updated on 25/Apr/21
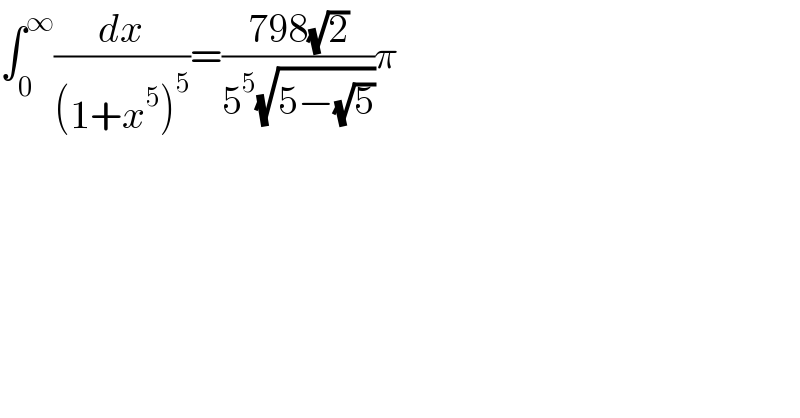
$$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{5}} \right)^{\mathrm{5}} }=\frac{\mathrm{798}\sqrt{\mathrm{2}}}{\mathrm{5}^{\mathrm{5}} \sqrt{\mathrm{5}−\sqrt{\mathrm{5}}}}\pi \\ $$
Answered by Ar Brandon last updated on 25/Apr/21
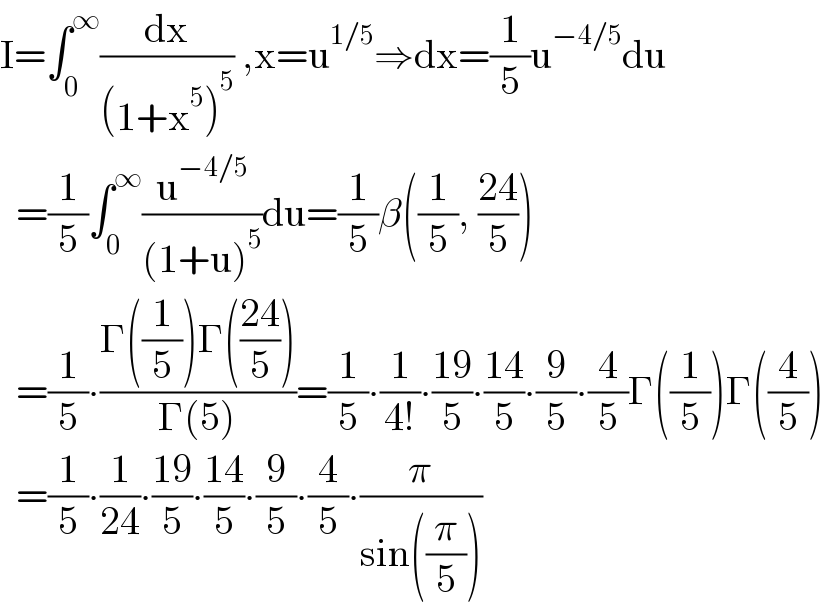
$$\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{5}} \right)^{\mathrm{5}} }\:,\mathrm{x}=\mathrm{u}^{\mathrm{1}/\mathrm{5}} \Rightarrow\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{5}}\mathrm{u}^{−\mathrm{4}/\mathrm{5}} \mathrm{du} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{5}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{u}^{−\mathrm{4}/\mathrm{5}} }{\left(\mathrm{1}+\mathrm{u}\right)^{\mathrm{5}} }\mathrm{du}=\frac{\mathrm{1}}{\mathrm{5}}\beta\left(\frac{\mathrm{1}}{\mathrm{5}},\:\frac{\mathrm{24}}{\mathrm{5}}\right) \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{5}}\centerdot\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{5}}\right)\Gamma\left(\frac{\mathrm{24}}{\mathrm{5}}\right)}{\Gamma\left(\mathrm{5}\right)}=\frac{\mathrm{1}}{\mathrm{5}}\centerdot\frac{\mathrm{1}}{\mathrm{4}!}\centerdot\frac{\mathrm{19}}{\mathrm{5}}\centerdot\frac{\mathrm{14}}{\mathrm{5}}\centerdot\frac{\mathrm{9}}{\mathrm{5}}\centerdot\frac{\mathrm{4}}{\mathrm{5}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{5}}\right)\Gamma\left(\frac{\mathrm{4}}{\mathrm{5}}\right) \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{5}}\centerdot\frac{\mathrm{1}}{\mathrm{24}}\centerdot\frac{\mathrm{19}}{\mathrm{5}}\centerdot\frac{\mathrm{14}}{\mathrm{5}}\centerdot\frac{\mathrm{9}}{\mathrm{5}}\centerdot\frac{\mathrm{4}}{\mathrm{5}}\centerdot\frac{\pi}{\mathrm{sin}\left(\frac{\pi}{\mathrm{5}}\right)} \\ $$
Commented by Dwaipayan Shikari last updated on 25/Apr/21

$${Thanks}!\:.{But}\:{another}\:{method}?\: \\ $$
Commented by Ar Brandon last updated on 25/Apr/21

$$\mathrm{You}\:\mathrm{can}\:\mathrm{do}\:\mathrm{the}\:\mathrm{partial}\:\mathrm{fraction}\:\mathrm{bro}.\:\mathrm{Haha}! \\ $$😄
Answered by MJS_new last updated on 25/Apr/21
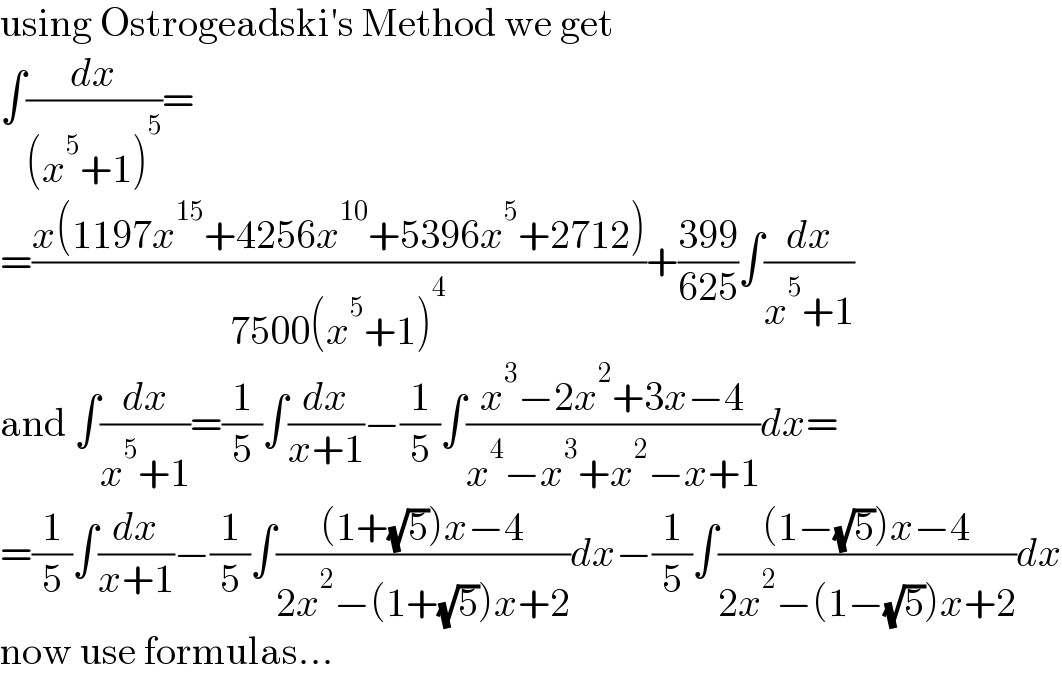
$$\mathrm{using}\:\mathrm{Ostrogeadski}'\mathrm{s}\:\mathrm{Method}\:\mathrm{we}\:\mathrm{get} \\ $$$$\int\frac{{dx}}{\left({x}^{\mathrm{5}} +\mathrm{1}\right)^{\mathrm{5}} }= \\ $$$$=\frac{{x}\left(\mathrm{1197}{x}^{\mathrm{15}} +\mathrm{4256}{x}^{\mathrm{10}} +\mathrm{5396}{x}^{\mathrm{5}} +\mathrm{2712}\right)}{\mathrm{7500}\left({x}^{\mathrm{5}} +\mathrm{1}\right)^{\mathrm{4}} }+\frac{\mathrm{399}}{\mathrm{625}}\int\frac{{dx}}{{x}^{\mathrm{5}} +\mathrm{1}} \\ $$$$\mathrm{and}\:\int\frac{{dx}}{{x}^{\mathrm{5}} +\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{5}}\int\frac{{dx}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{5}}\int\frac{{x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{4}}{{x}^{\mathrm{4}} −{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\int\frac{{dx}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{5}}\int\frac{\left(\mathrm{1}+\sqrt{\mathrm{5}}\right){x}−\mathrm{4}}{\mathrm{2}{x}^{\mathrm{2}} −\left(\mathrm{1}+\sqrt{\mathrm{5}}\right){x}+\mathrm{2}}{dx}−\frac{\mathrm{1}}{\mathrm{5}}\int\frac{\left(\mathrm{1}−\sqrt{\mathrm{5}}\right){x}−\mathrm{4}}{\mathrm{2}{x}^{\mathrm{2}} −\left(\mathrm{1}−\sqrt{\mathrm{5}}\right){x}+\mathrm{2}}{dx} \\ $$$$\mathrm{now}\:\mathrm{use}\:\mathrm{formulas}... \\ $$
Commented by Dwaipayan Shikari last updated on 25/Apr/21

$${Thanks}\:{sir}! \\ $$
Commented by MJS_new last updated on 25/Apr/21
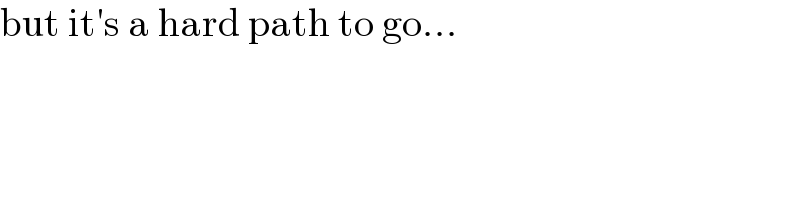
$$\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{a}\:\mathrm{hard}\:\mathrm{path}\:\mathrm{to}\:\mathrm{go}... \\ $$
