Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 139590 by EnterUsername last updated on 29/Apr/21

If a, b and c are integers not all simultaneously equal and w≠1 is a cube root of unity, then the minimum value of ∣a+bw+cw^2 ∣ is (A) 0 (B) 1 (C) (√3)/2 (D) 1/2

$$\mathrm{If}\:{a},\:{b}\:\mathrm{and}\:{c}\:\mathrm{are}\:\mathrm{integers}\:\mathrm{not}\:\mathrm{all}\:\mathrm{simultaneously}\:\mathrm{equal} \\ $$$$\mathrm{and}\:{w}\neq\mathrm{1}\:\mathrm{is}\:\mathrm{a}\:\mathrm{cube}\:\mathrm{root}\:\mathrm{of}\:\mathrm{unity},\:\mathrm{then}\:\mathrm{the}\:\mathrm{minimum} \\ $$$$\mathrm{value}\:\mathrm{of}\:\mid{a}+{bw}+{cw}^{\mathrm{2}} \mid\:\mathrm{is}\: \\ $$$$\left(\mathrm{A}\right)\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\left(\mathrm{B}\right)\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\left(\mathrm{C}\right)\:\sqrt{\mathrm{3}}/\mathrm{2}\:\:\:\:\:\:\:\:\:\:\left(\mathrm{D}\right)\:\mathrm{1}/\mathrm{2} \\ $$

Answered by MJS_new last updated on 29/Apr/21

∣a+bw+cw^2 ∣= [w=−(1/2)±((√3)/2)i] =(√(a^2 +b^2 +c^2 −(ab+ac+bc)))=A (a, b, c) (d/dc)[A (a, b, c)]=0 ⇒ c=((a+b)/2) A (a, b, ((a+b)/2)) =((√3)/2)∣a−b∣ since b=a ⇒ c=a is not allowed and a,b ∈Z the minimum is at ∣a−b∣=1 ⇒ answer is ((√3)/2)

$$\mid{a}+{bw}+{cw}^{\mathrm{2}} \mid= \\ $$$$\:\:\:\:\:\left[{w}=−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right] \\ $$$$=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\left({ab}+{ac}+{bc}\right)}={A}\:\left({a},\:{b},\:{c}\right) \\ $$$$\frac{{d}}{{dc}}\left[{A}\:\left({a},\:{b},\:{c}\right)\right]=\mathrm{0}\:\Rightarrow\:{c}=\frac{{a}+{b}}{\mathrm{2}} \\ $$$${A}\:\left({a},\:{b},\:\frac{{a}+{b}}{\mathrm{2}}\right)\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mid{a}−{b}\mid \\ $$$$\mathrm{since}\:{b}={a}\:\Rightarrow\:{c}={a}\:\mathrm{is}\:\mathrm{not}\:\mathrm{allowed}\:\mathrm{and}\:{a},{b}\:\in\mathbb{Z} \\ $$$$\mathrm{the}\:\mathrm{minimum}\:\mathrm{is}\:\mathrm{at}\:\mid{a}−{b}\mid=\mathrm{1}\:\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$

Commented by EnterUsername last updated on 29/Apr/21

Thanks Sir. I′ve understood your method. But author′s choice is (B). Do you think it′s a mistake ?

$$\mathrm{Thanks}\:\mathrm{Sir}.\:\mathrm{I}'\mathrm{ve}\:\mathrm{understood}\:\mathrm{your}\:\mathrm{method}.\:\mathrm{But}\:\mathrm{author}'\mathrm{s} \\ $$$$\mathrm{choice}\:\mathrm{is}\:\left(\mathrm{B}\right).\:\mathrm{Do}\:\mathrm{you}\:\mathrm{think}\:\mathrm{it}'\mathrm{s}\:\mathrm{a}\:\mathrm{mistake}\:? \\ $$

Commented by EnterUsername last updated on 29/Apr/21

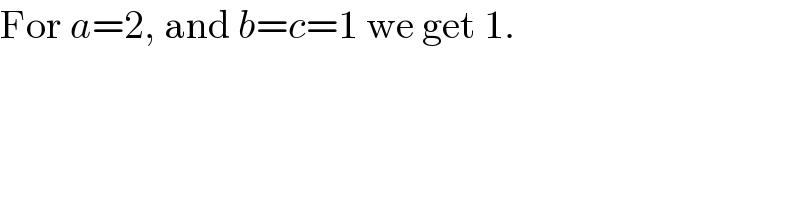
For a=2, and b=c=1 we get 1.

$$\mathrm{For}\:{a}=\mathrm{2},\:\mathrm{and}\:{b}={c}=\mathrm{1}\:\mathrm{we}\:\mathrm{get}\:\mathrm{1}. \\ $$

Commented by MJS_new last updated on 29/Apr/21

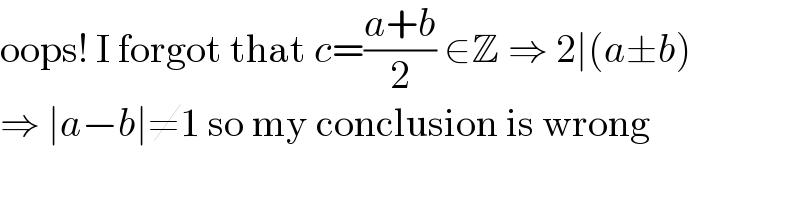
oops! I forgot that c=((a+b)/2) ∈Z ⇒ 2∣(a±b) ⇒ ∣a−b∣≠1 so my conclusion is wrong

$$\mathrm{oops}!\:\mathrm{I}\:\mathrm{forgot}\:\mathrm{that}\:{c}=\frac{{a}+{b}}{\mathrm{2}}\:\in\mathbb{Z}\:\Rightarrow\:\mathrm{2}\mid\left({a}\pm{b}\right) \\ $$$$\Rightarrow\:\mid{a}−{b}\mid\neq\mathrm{1}\:\mathrm{so}\:\mathrm{my}\:\mathrm{conclusion}\:\mathrm{is}\:\mathrm{wrong} \\ $$

Commented by EnterUsername last updated on 29/Apr/21

OK. Thank you Sir 😃

$$\mathrm{OK}.\:\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir} \\ $$😃

Commented by mr W last updated on 29/Apr/21

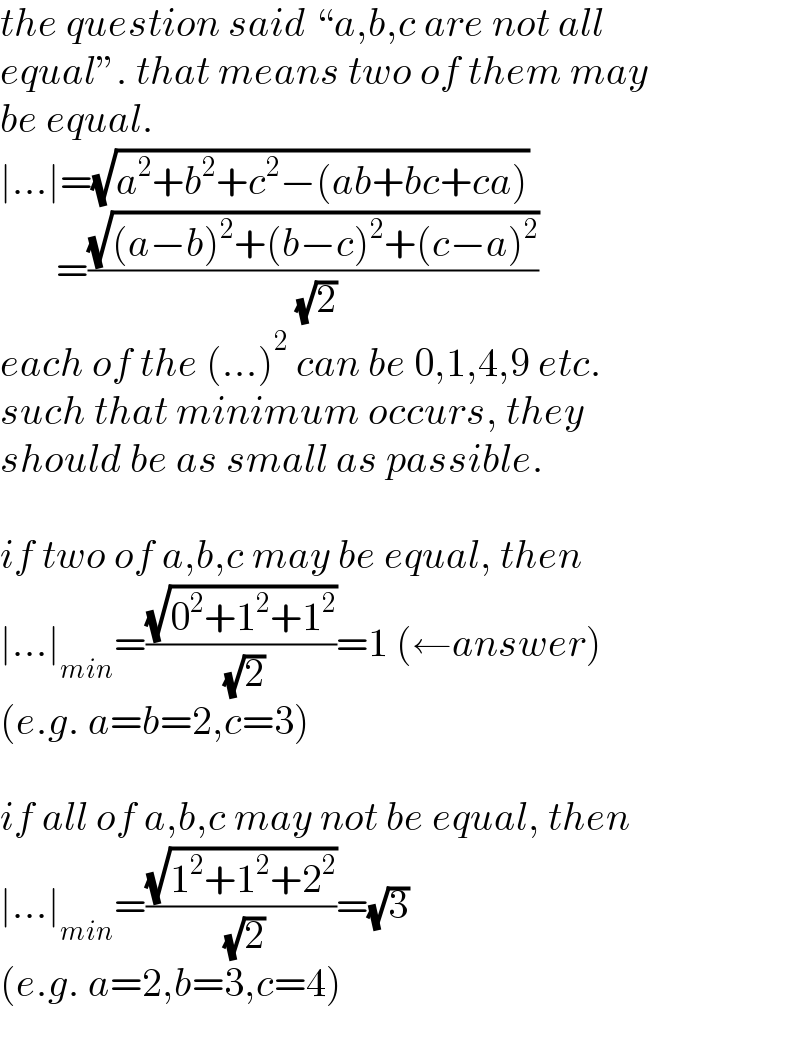
the question said “a,b,c are not all equal”. that means two of them may be equal. ∣...∣=(√(a^2 +b^2 +c^2 −(ab+bc+ca))) =((√((a−b)^2 +(b−c)^2 +(c−a)^2 ))/( (√2))) each of the (...)^2 can be 0,1,4,9 etc. such that minimum occurs, they should be as small as passible. if two of a,b,c may be equal, then ∣...∣_(min) =((√(0^2 +1^2 +1^2 ))/( (√2)))=1 (←answer) (e.g. a=b=2,c=3) if all of a,b,c may not be equal, then ∣...∣_(min) =((√(1^2 +1^2 +2^2 ))/( (√2)))=(√3) (e.g. a=2,b=3,c=4)

$${the}\:{question}\:{said}\:``{a},{b},{c}\:{are}\:{not}\:{all} \\ $$$${equal}''.\:{that}\:{means}\:{two}\:{of}\:{them}\:{may} \\ $$$${be}\:{equal}. \\ $$$$\mid...\mid=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\left({ab}+{bc}+{ca}\right)} \\ $$$$\:\:\:\:\:\:\:=\frac{\sqrt{\left({a}−{b}\right)^{\mathrm{2}} +\left({b}−{c}\right)^{\mathrm{2}} +\left({c}−{a}\right)^{\mathrm{2}} }}{\:\sqrt{\mathrm{2}}} \\ $$$${each}\:{of}\:{the}\:\left(...\right)^{\mathrm{2}} \:{can}\:{be}\:\mathrm{0},\mathrm{1},\mathrm{4},\mathrm{9}\:{etc}. \\ $$$${such}\:{that}\:{minimum}\:{occurs},\:{they} \\ $$$${should}\:{be}\:{as}\:{small}\:{as}\:{passible}.\: \\ $$$$ \\ $$$${if}\:{two}\:{of}\:{a},{b},{c}\:{may}\:{be}\:{equal},\:{then} \\ $$$$\mid...\mid_{{min}} =\frac{\sqrt{\mathrm{0}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }}{\:\sqrt{\mathrm{2}}}=\mathrm{1}\:\left(\leftarrow{answer}\right) \\ $$$$\left({e}.{g}.\:{a}={b}=\mathrm{2},{c}=\mathrm{3}\right) \\ $$$$ \\ $$$${if}\:{all}\:{of}\:{a},{b},{c}\:{may}\:{not}\:{be}\:{equal},\:{then} \\ $$$$\mid...\mid_{{min}} =\frac{\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }}{\:\sqrt{\mathrm{2}}}=\sqrt{\mathrm{3}} \\ $$$$\left({e}.{g}.\:{a}=\mathrm{2},{b}=\mathrm{3},{c}=\mathrm{4}\right) \\ $$

Commented by EnterUsername last updated on 29/Apr/21

Thank you Sir !

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}\:! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com