
Question Number 140221 by qaz last updated on 05/May/21
![∫_0 ^∞ x^2 [ln(1+e^x )−x]dx=((7π^4 )/(360))](Q140221.png)
$$\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{2}} \left[{ln}\left(\mathrm{1}+{e}^{{x}} \right)−{x}\right]{dx}=\frac{\mathrm{7}\pi^{\mathrm{4}} }{\mathrm{360}} \\ $$
Answered by Dwaipayan Shikari last updated on 05/May/21
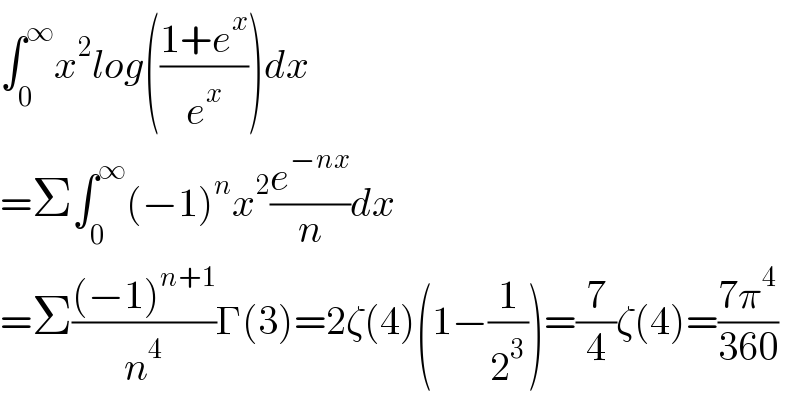
$$\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{2}} {log}\left(\frac{\mathrm{1}+{e}^{{x}} }{{e}^{{x}} }\right){dx} \\ $$$$=\Sigma\int_{\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}} \frac{{e}^{−{nx}} }{{n}}{dx} \\ $$$$=\Sigma\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}^{\mathrm{4}} }\Gamma\left(\mathrm{3}\right)=\mathrm{2}\zeta\left(\mathrm{4}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }\right)=\frac{\mathrm{7}}{\mathrm{4}}\zeta\left(\mathrm{4}\right)=\frac{\mathrm{7}\pi^{\mathrm{4}} }{\mathrm{360}} \\ $$
Commented by qaz last updated on 05/May/21

$${thank}\:{you}\:{sir} \\ $$
